Velocity-porosity relationships in oceanic basalt from eastern flank of the Juan de Fuca Ridge: The effect of crack closure on seismic velocity
Takeshi Tsuji 1 3 Gerardo J. Iturrino 21 Department of Civil and Earth Resources Engineering, Kyoto University, Katsura Campus, Nishikyo-ku, Kyoto 615-8540, Japan.
2 Lamont-Doherty Earth Observatory of Columbia University, P.O. Box 1000, 61 Route 9W Palisades, NY 10964-1000, USA.
3 Corresponding author. Email: tsuji@earth.kumst.kyoto-u.ac.jp
Exploration Geophysics 39(1) 41-51 https://doi.org/10.1071/EG08001
Submitted: 7 August 2007 Accepted: 14 December 2007 Published: 5 March 2008
Abstract
To construct in situ velocity-porosity relationships for oceanic basalt, considering crack features, P- and S-wave velocity measurements on basaltic samples obtained from the eastern flank of the Juan de Fuca Ridge were carried out under confining pressures up to 40 MPa. Assuming that the changes in velocities with confining pressures are originated by micro-crack closure, we estimated micro-crack aspect ratio spectra using the Kuster-Toksöz theory. The result demonstrates that the normalised aspect ratio spectra of the different samples have similar characteristics. From the normalised aspect ratio spectrum, we then constructed theoretical velocity-porosity relationships by calculating an aspect ratio spectrum for each porosity. In addition, by considering micro-crack closure due to confining pressure, a velocity-porosity relationship as a function of confining pressure could be obtained. The theoretical relationships that take into account the aspect ratio spectra are consistent with the observed relationships for over 100 discrete samples measured at atmospheric pressure, and the commonly observed pressure dependent relationships for a wide porosity range. The agreement between the laboratory-derived data and theoretically estimated values demonstrates that the velocity-porosity relationships of the basaltic samples obtained from the eastern flank of the Juan de Fuca Ridge, and their pressure dependence, can be described by the crack features (i.e. normalised aspect ratio spectra) and crack closure.
Key words: velocity-porosity relationship, oceanic basalt, crack aspect ratio, Kuster-Toksöz theory, and Integrated Ocean Drilling Program.
Acknowledgments
We are grateful to IODP Expedition 301 scientists and crews, especially to Co-chief Scientists Andrew Fisher (University California, Santa Cruz) and Tetsuro Urabe (University Tokyo), Staff Scientist Adam Klaus (Texas A&M University), and Shipboard Scientists Anne Bartetzko (University Bremen), Shusaku Goto (Kyoto University), Michael Hutnak (University California, Santa Cruz), and Mark Nielsen (Oregon State University). We also thank two anonymous reviewers for their helpful comments and suggestions. Furthermore, we also thank Fumio Kono and Tatsuo Saeki (TRC, JOGMEC) for the measurement of velocities. This research used samples and data provided by the Integrated Ocean Drilling Program (IODP). The United States Science Support Program supported part of this research. This research was partly supported by the Japan Agency for Marine-Earth Science and Technology (JAMSTEC) and Japan Drilling Earth Science Consortium (J-DESC).
Alt, J. C., Honnorez, J., Laverne, C., and Emmermann, R., 1986, Hydrothermal alteration of a 1 km section through the upper oceanic crust, Deep Sea Drilling Project hole 504B: mineralogy, chemistry, and evolution of seawater-basalt interactions: Journal of Geophysical Research 91, 10309–10335.
| Crossref | GoogleScholarGoogle Scholar |
Cheng, C. H., and Toksöz, M. N., 1979, Inversion of seismic velocities for the pore aspect ratio spectrum of a rock: Journal of Geophysical Research 84, 7533–7543.
| Crossref | GoogleScholarGoogle Scholar |
Fisher, A. T., Becker, K., and Davis, E. E., 1997, The permeability of young oceanic crust east of Juan de Fuca Ridge determined using borehole thermal measurements: Geophysical Research Letters 24, 1311–1314.
| Crossref | GoogleScholarGoogle Scholar |
Johnston, D. H., Toksöz, M. N., and Timur, A., 1979, Attenuation of seismic waves in dry and saturated rocks. II: Mechanisms: Geophysics 44, 691–711.
| Crossref | GoogleScholarGoogle Scholar |
Shearer, P. M., 1988, Cracked media, Poisson’s ratio and the structure of the upper oceanic crust: Geophysical Journal 92, 357–362.
| Crossref | GoogleScholarGoogle Scholar |
Walsh, J. B., 1966, Seismic attenuation in rock due to friction: Journal of Geophysical Research 71, 2591–2599.
Wilkens, R. H., Fryer, G. J., and Karsten, J., 1991, Evolution of porosity and seismic structure of upper oceanic crust: importance of aspect ratios: Journal of Geophysical Research 96, 17891–17995.
| Crossref | GoogleScholarGoogle Scholar |
Appendix: P-wave quality factor
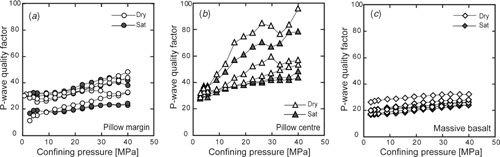
Quality factor is another important acoustic property obtained from laboratory measurements and is closely related to crack intensity, mineral composition, and mineral textures (e.g. Johnston et al., 1979). P-wave quality factors (Figure A) were calculated from the stored signal waveforms (Figure 4) using a spectrum division technique (Toksöz et al., 1979). In order to ensure similar coupling and pressure conditions for both the sample and a reference standard, the signals from an aluminum cylinder of the same sample size were recorded at various pressure steps and used as reference signals. Measurements were carried out in both saturated and dry conditions. The calculated quality factors are affected by many attenuation mechanisms (e.g. matrix inelasticity, viscosity and flow of saturating fluids, and scattering from inclusions), and we cannot fully account for each attenuation mechanism.
|
The P-wave quality factors increase with confining pressure, mainly due to closure of micro-cracks, and the trend suggests that values would increase further beyond the maximum pressure (40 MPa) used in the experiment. As a result of micro-crack closure with increasing confining pressure, the frictional dissipation due to relative motions at the grain boundaries and across crack surfaces (Walsh, 1966) becomes small. Furthermore, most P-wave quality factors measured in saturated basaltic samples are lower than those of dry samples (Figure A) because the fluid-associated attenuation is not considered when dealing with dry conditions (e.g. Johnston et al., 1979).
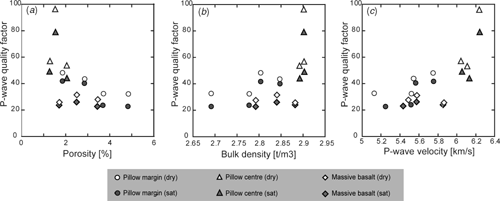
We can find a clear relationship between quality factor and porosity (Figure B-a), similar to that previously reported by Wepfer and Christensen (1991) where quality factor increases rapidly with decreasing porosity. The high quality factor near zero porosity may indicate that the grain mineral inelasticity is very low. In addition, quality factor-velocity relationships (Figure B-c) clearly show that P-wave quality factors increase rapidly (nonlinearly) with velocities.
|
As in the case of the velocities, P-wave quality factors for centre parts of pillow basalts are higher than those obtained from the pillow margins (Figure A), whereas P-wave quality factors of the massive basalts are lower than those of the pillow basalts. The relationship between quality factors and porosities (Figure B) further demonstrate that the massive basalts have low quality factors, compared to pillow basalts with similar porosities. One possible explanation for this is that significant scattering occurs at the 1 MHz source frequency (e.g. Johnston et al., 1979; Hudson, 1981) because of the relatively larger grain sizes in the groundmass of the massive basalts (Tsuji and Yamaguchi, 2007).
P-wave quality factors have an average value of ~31 at a confining pressure of 5.5 MPa, which corresponds to in situ effective pressure. Tompkins and Christensen (1999) reported that P-wave quality factors of the dredged samples of Juan de Fuca Ridge are 11–17 at hydrostatic pore pressure. The discrepancy in P-wave quality factors between the two studies could be attributed to the fact that the samples from the Tompkins and Christensen (1999) study were obtained from seafloor dredges, whereas the samples used in this study were obtained at 100 km off axis of the Juan de Fuca Ridge and in situ below an ~265 m thick sedimentary cover. Furthermore, the difference may represent lateral variations away from ridge crests and different degrees of alteration associated with water-rock interactions at their respective locations. In addition, quality factor measurements are highly dependent on several parameters including strain amplitude (Johnston et al., 1979) as well as the measurement technique; when comparing to the quality factor of low-frequency seismic data, we also need to consider the scale (source frequency) differences. Therefore, it is difficult to compare results from different studies in a quantitatively manner.

