A ‘simplest’ steady-state Munch-like model of phloem translocation, with source and pathway and sink
William F. Pickard A B and Barbara Abraham-Shrauner AA Department of Electrical and Systems Engineering, Washington University, St Louis, MO 63130, USA.
B Corresponding author. Email: wfp@ese.wustl.edu
Functional Plant Biology 36(7) 629-644 https://doi.org/10.1071/FP08278
Submitted: 29 October 2008 Accepted: 26 March 2009 Published: 2 July 2009
Abstract
In the 80 years since its introduction by Münch, the pressure-driven mass-flow model of phloem translocation has become hegemonic, and has been mathematically modelled in many different fashions but not, to our knowledge, by one that incorporated the equations of hydrodynamics with those of osmosis and slice-source and slice-sink boundary conditions to yield a system that admits of an analytical steady-state solution for the sap velocity in a single sieve tube. To overcome this situation, we drastically simplified the problem by: (i) justifying a low Peclet number idealisation in which transverse variations could be neglected; (ii) justifying a low viscosity idealisation in which axial pressure drops could be neglected; and (iii) assuming a sink of strength sufficient to lower the photosynthate concentration at the extreme distal end of the sieve tube to levels at which it became unimportant. The resulting ordinary nonlinear second-order differential equation in sap velocity and axial position was of a generalised Liénard form with a single forcing parameter; and this is reason enough for the lack of a known analytic solution. However, since the forcing parameter was very large, it was possible to deduce approximate second-order solutions for behavior in the source, sink and transport regions: the sap velocity is zero at the slice-source, climbs with exponential rapidity to a plateau, maintains this plateau over most of the sieve tube, and then drops with exponential rapidity to zero at the slice-sink.
Additional keywords: biological fluid mechanics, Liénard equation, Münch mechanism, osmosis, phloem transport.
Acknowledgements
We thank Matthew V. Thompson for reading our manuscript, making helpful suggestions and diligently provoking us to greater transparency for the benefit non-mathematical readers.
Initially, we note that the physically expected downward-concavity of u(z) requires u″ < 0; and, therefore, even if the ψ′ term on the right hand side of Eqn (13) does not swamp the u term, it must at least outweigh it. By Eqn (14) the condition for neglecting the ‘pressure’ terms of Eqns (8) and (13) is where a typical Table 1 value for the term in curly braces is roughly 1/7. In all ω(ζ) computations successfully conducted, ω## was non-positive and ω non-negative, as expected. For Ξ = 1000, the range of the ratio of Eqn (A1) was (0,0.1427); for Ξ = 100, 10 and 1, it was (0,0.0339), (0,0.0206) and (0,0.0186), respectively. This trend is not unexpected because study of a progression of ω(ζ) plots shows that, with increasing Ξ, the mid-regions of the plots flatten to a plateau while the edges of the plateau become markedly steeper; this can be seen in Fig. 4. We conclude that neglect of the p′(z) term is justified. Moreover, for this qualitative study, its neglect enormously simplifies the problem. As caveats for the reader, we note two further numerical observations. First, for Ξ = 10 000, the range of the ratio is (0,14.9548); this could be interpreted as an artifact of computational roundoff. Second, if one began the integration at ζ = 1 and shot backwards towards the origin, the problem of meeting the two boundary conditions at ζ = 1 of course went away: but ω## developed a small non-negative region for Ξ > 400, which conceivably could be computational error manifesting itself differently; and, again for Ξ > 400, both computational stability and desired behaviour near the shot-at-boundary became more serious issues than for the preferred method of shooting forward from ζ = 0. The conspicuous linearity displayed in Fig. 3 by the dimensionless osmolality [ω# − κ] coupled with the boundary conditions Eqn (20) leads one to approximate the dimensionless speed as Back-substituting this equation into Eqn (19) yields Therefore, the approximation should be qualitatively useful for Ξ and The actual numerical values for Ξ = 1 are κ = −0.4844, ωmax = 0.1189 and [ω#(0) − κ] = 0.9615. For Ξ = 0.1 they are κ = −0.0498, ωmax = 0.0124 and [ω#(0) − κ] = 0.0996. These considerations for unrealistically small Ξ reveal that, for sufficiently large D (or small ϒ), the expected diffusion-like osmolality profile does appear. They also give us confidence that our numerical integration does indeed work properly when Ξ is non-large and validate its usefulness for guiding our development of asymptotic solutions. A series of the form ΣAnexp(–αnχ), where the αn are real non-negative constants and χ is a real variable, is a particular case of what are called Dirichlet series (Mandelbrojt 1972); it is known that, if the series converges for χ = 0, then it converges for all χ > 0. Figure 5 and the developments of the Accessory Publication to this paper lead one to believe that ω(χ) displays a prominently exponential behavior and might readily be represented using a Dirichlet series. To examine this intuition, let αn = nΛ (n = 0, 1, 2, …), where Λ > 0 is a finite real decay parameter not yet specified and express the speed as The differential equation for the speed is (19) which may be written as where * denotes d/dχ and χ = ξ = 1 − ζ when the + sign is selected but χ = ζ when the − sign is chosen. The + sign is appropriate near the boundary at ζ = 1 where the independent variable ξ = 1 − ζ is preferable; the −; sign is appropriate near the boundary at ζ = 0 where the preferable independent variable is ζ itself. Next define so that 1 ≧ τ ≧ e−Λ > 0. Then, defining ω+ = dω/dτ, rewrite (C2) as the first order system: Because this system satisfies Lipschitz conditions over 1 ≧ τ ≧ e−Λ > 0, both ω and ω+ possess unique continuous solutions over this interval and will satisfy arbitrary initial conditions at τ = 1 (Ince 1956, s. 3.3). If (C4b) is differentiated repeatedly, it will be observed that the higher order derivatives are well defined ratios of polynomials over the envisioned range and able to meet the Lipschitz conditions. Thus ω++, ω+++, etc. will also be well defined. Therefore, over our range of interest, we can utilise Taylor-Dirichlet expansions of the form although the rate of convergence of the series is not guaranteed. The structure of the system will become clearer if extensive substitutions are made: and Substitution of (C5) and (C6) into (C2) then yields, upon grouping, a series of terms, each of the form where the summation extends over all combinations of p and q such that Consider first n = 0. In Eqn (C7) setting to zero the term in brackets yields as might have been expected from Eqn (S6) of the Accessory Publication to this paper. Since the ± sign does not appear in (C8), it follows that both the ξ-expansion and the χ-expansion yield the same plateau region far from the ends of the sieve tube. This is encouraging. Next consider n = 1. Here (C7) yields Now consider n = 2. Here (C7) yields If and
(C11a) expresses (20b) in the present notation and (C11b) expresses (20c) and (C11c) expresses (C2). Since, to order 2,
(C12b) and (C12c) combine to yield
(C8), (C13a) and (C13b) then combine with (C12a) to yield
(C9) and (C14) can then be combined to show that Moreover, this value of From (C15) it can be predicted that κ(1000) = −114.04; the value derived by numerical integration is −113.83. Moreover, the plot of ω(ζ) given in Fig. 4 predicts that the distance-of-rise near ζ = 0 is roughly twice the distance-of-fall near z = 1; and this is in accord with the Using (C13) and the calculated values of and The value of This is sufficient for predictions of (C17) to be used along with (C7) for qualitative studies of convergence of Taylor-Dirichlet series (C5). As a practical matter, it seems probable that only terms of orders 0 and 1 will be needed throughout the transport phloem, because term-1 dies off exponentially quickly and the total contribution of the other terms should be negligible. Finally, the simplification from Eqn (18f) to Eqn (19) depended upon assumed inequality which (using |κ| ∼ Ξ2/3 and the values of Table 1) requires υarb ≪ 4. Thus, the simplification leading to Eqn (19) is probably justified; or, at the least, it is a good enough approximation to have justified the analysis lavished upon it, because it is almost always the case that υarb
Bluman GW, Cole JD
(1969) The general similarity solution of the heat equation. Journal of Mathematics and Mechanics 18, 1025–1042.
to Peters et al. 2007, 2008) and a biophysical background in both the ascent of sap (Pickard 1981) and osmotic swelling (Pickard 2008).
3The logic of this assertion is not a priori obvious, especially since the anatomy of the phloem might encourage one to favor a fully three dimensional formulation. Having initially attempted some small generalisation in this direction, we feel that neglecting intra-tube variations in the transverse plane really is necessary and will greatly simplify matters for the reader. This is basically an application of the Variation of the Problem technique favored by mathematicians confronted with stubborn problems (e.g. Polya 1957, p. 209). Besides, the nature of the generalisation from one dimension is not a priori obvious; and, physiologically, phloem experiments normally report only axial variations along a phloem bundle.
4In science and engineering, a ‘dimensionless group’ is ‘the product of a subset of a problem’s dimensioned parameters which is itself dimensionless’. Generally, a problem will have far fewer useful dimensionless groups than it has parameters. Also, as a rule of thumb, exploring a dependent variable’s behavior is much simpler using its dimensionless groups than its more numerous parameters. A standard and still useful treatise on the topic is the monograph of Langhaar (1951).
5‘Analytical’, as it will be used in this paper, refers to a function or system of equations which is treated by the methods of algebra and calculus and yields results as formulas expressed in computable algebraic functions which have neither discontinuities nor infinities over the range of interest. In contrast, a ‘numerical’ method yields no formulas but rather numerical predictions. Philosophically, an analytic method is generally preferred if one is seeking thorough understanding of an idealised problem. Whereas a numerical method may be more appropriate when seeking usable predictions about a practical situation.
6Sieve tube sap is a complex substance which varies widely from season to season and species to species (cf. Ziegler 1975). It contains, among others, inorganic ions, amino acids, and raffinose family oligosaccharides. As a simplification, we shall speak only of ‘an osmolyte’ and pick sucrose as illustrative of this substance.
7The parameter Ξ will turn out to be linear in the product (source strength) × (plasmalemmal water permeability). Intuitively, non-zero values of both are required for phloem transport to take place by way of a Münch-like mechanism. Since the boundary conditions (Eqn 20) involve neither, the only way either source strength or plasmalemma permeability enters is by way of Ξ. Hence, phloem transport can be said to be ‘driven’ or ‘forced’ by Ξ.
8We argue that copious output from a computer program, although desirable in an agronomic prediction, is less desirable in a setting which requires deep inward digestion of recondite concepts to appreciate the qualitative variations of a complicated process. For example, a numerical model can show that some quantity may increase rapidly with time: but we believe that achieving an intuitive grasp of the process would be facilitated by additional knowledge that the variation is exponential with an algebraically expressible rise time.
9We note that what makes a sink a sink is the proclivity of nearby tissue to take up photosynthate. To a ‘pure’ applied mathematician looking for a boundary condition which would simplify analysis, this at once suggests taking this uptake to the limit υarb = 0. Since the sieve tube is not a storage tissue with an imperative to accumulate photosynthate, and since our interest is more qualitative understanding of mechanism than quantitative prediction, we would concur with such a choice.
Appendices
Appendix A: Is neglect of the p′(z) term justified?

Appendix B: Behaviour of ω for Ξ
![]() 1
1


![]() 1 and implies that
1 and implies that


Appendix C: Dirichlet series expansion for non-small Ξ




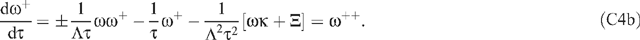






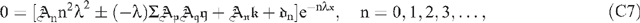
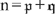 and where
and where 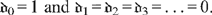 . In the abstract, the problem has now been solved to any order of approximation N. However, solving for the N + 1 unknown coefficients
. In the abstract, the problem has now been solved to any order of approximation N. However, solving for the N + 1 unknown coefficients 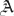 n plus λ and
n plus λ and 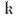 is harder than might be thought because it turns out not to be possible to do a simple recursion up the chain of coefficients and then apply boundary conditions as an afterthought to determine λ and
is harder than might be thought because it turns out not to be possible to do a simple recursion up the chain of coefficients and then apply boundary conditions as an afterthought to determine λ and 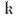 . One will always need N+3 independent relations among the unknowns, but they need not include all of the first N+1 instances of (C7).
. One will always need N+3 independent relations among the unknowns, but they need not include all of the first N+1 instances of (C7).
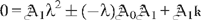 , which, being homogeneous, cannot determine
, which, being homogeneous, cannot determine 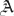 1 and instead constrains λ:
1 and instead constrains λ:

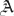 1 were known, one could efficiently recurse using (C7) to find higher order coefficients. However, it is not. Therefore, we shall proceed to the 2nd order not by invoking (C10) but rather (i) by focussing on the ξ-solution and (ii) by imposing three boundary conditions at
1 were known, one could efficiently recurse using (C7) to find higher order coefficients. However, it is not. Therefore, we shall proceed to the 2nd order not by invoking (C10) but rather (i) by focussing on the ξ-solution and (ii) by imposing three boundary conditions at 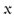 = 0:
= 0:


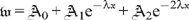 ,
,





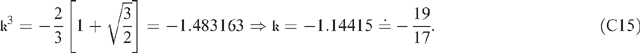
 can be back-substituted into (C9) to show that
can be back-substituted into (C9) to show that

 derivable from Eqns (C16). However, the value of Λ(10 000) measured from Fig. 5 is 17.6 in contrast to the 15.4 predicted from (C16b).
derivable from Eqns (C16). However, the value of Λ(10 000) measured from Fig. 5 is 17.6 in contrast to the 15.4 predicted from (C16b).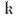 and λ
and λ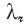 yields, for the expansion near ζ = 1, the coefficients
yields, for the expansion near ζ = 1, the coefficients


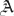 2 predicted from Eqn (C10) using (C17a) and (C17b) is
2 predicted from Eqn (C10) using (C17a) and (C17b) is

![]() 1 (Zimmermann and Ziegler 1975).
1 (Zimmermann and Ziegler 1975).



