The evolution of morphogenetic fitness landscapes: conceptualising the interplay between the developmental and ecological drivers of morphological innovation
Charles R. MarshallDepartment of Integrative Biology and University of California Museum of Paleontology, University of California, Berkeley, CA 94720, USA. Email: crmarshall@berkeley.edu
Australian Journal of Zoology 62(1) 3-17 https://doi.org/10.1071/ZO13052
Submitted: 11 July 2013 Accepted: 8 January 2014 Published: 13 February 2014
Journal Compilation © CSIRO Publishing 2014 Open Access CC BY-NC-ND
Abstract
Here I show how fitness landscapes can be used to understand the relative importance of developmental and ecological change in initiating morphological innovation. Key is the use of morphogenetic ‘rules’ as the axes of the landscape, which enables explicit incorporation of the contribution that specific morphologies make to fitness. Four modes of fitness landscape evolution are identified: (1) change in the density of peaks on the landscape, driven by an increase in the number of selective pressures encountered; (2) change in the dimensionality of the landscape through the addition of morphogenetic rules; (3) change in the size of one or more dimensions of the landscape through elaboration of already existing morphogenetic rules; and, (4) shifting the position of peaks in the landscape. Morphological innovation is initiated by ecological change in Mode (1), for example the Cambrian explosion of animals, and Mode (4), for example, when taxa such as sticklebacks make a shift in environment, or during coevolutionary escalation. Morphological change is initiated by developmental innovation for Mode (2), typified by some macroevolutionary innovations, such as the emergence of jaws, and in Mode (3), for example, in the differentiation of flower morphology facilitated by gene duplication of the B-class developmental genes.
Introduction
Morphological change and innovation pervade the fossil record. Most change is relatively minor, constituting the first appearance of new character states of existing characters, or, as clades become older, an increasing reshuffling of already-seen character states (Wagner 2000). Change of this magnitude is usually reflected in the recognition of new species or genera. Less frequent are morphological innovations that require the definition of new characters, which traditionally led to the erection of higher taxa in the Linnaean hierarchy.
What are the causes of morphological change and innovation from the mundane to the impressive? We know that changes in development must be involved, but changes in the biotic and physical environments must also be important. What is the relationship between these factors? Here I provide a conceptual framework that enables generalities to be drawn about the fundamental drivers of morphological change. The core of the framework is the morphogenetic fitness landscape.
Fitness landscapes: genotypic versus morphogenetic
Genotypic fitness landscapes
Fitness landscapes have a long and venerable history, dating to Wright (1931, 1932). Typically the ‘spatial’ component of the landscape is defined by a set of genes and their alleles. However, Simpson (1944, 1953), Lande (1976, 1979) and Arnold et al. (2001), among others, used the ‘spatial’ component of Wright’s landscapes to represent the phenotype. The resulting landscapes are typically termed adaptive landscapes (Pigliucci 2012), although Simpson (1944) called them selective landscapes (see also Brodie et al. 1995).
In genotypic fitness landscapes each dimension of the landscape represents a specific gene, with the different alleles corresponding to different positions along that dimension. Thus, each point on the landscape corresponds to a unique set of alleles. The altitude, or elevation, of each point corresponds to the fitness for that combination of alleles.
From a morphological perspective genotypic landscapes are of limited use; even for living species the mapping of the genotype into the phenotype is all but intractably complex (Lewontin 1974), even though great progress is being made towards an understanding of the genetic underpinnings of specific morphological changes (see Chan et al. (2010) for just one example, on pelvic reduction in sticklebacks, and Jones et al. (2012) for whole-genome analysis of adaptive evolution in sticklebacks).
Morphogenetic fitness landscapes
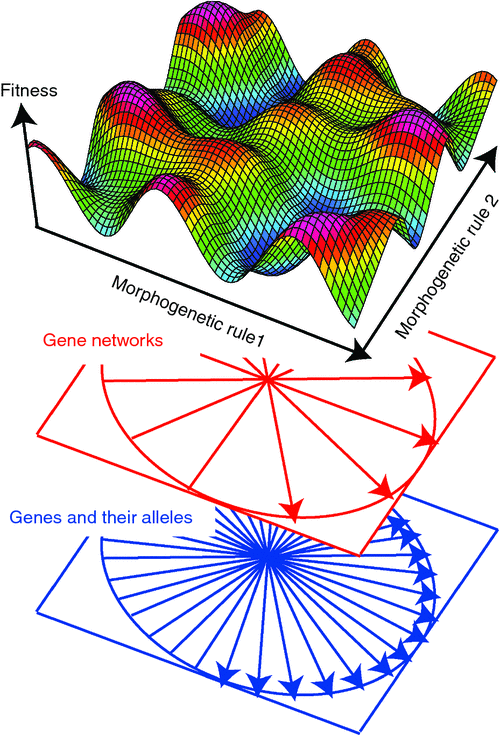
The ‘spatial’ dimensions of fitness landscapes may also be defined by morphogenetic rules (Raup 1966; Niklas 1994, 1997, 2004; Gerhart and Kirschner 1997; McGhee 1999, 2007), where each dimension corresponds to a specific morphogenetic rule, and where the position along each dimension corresponds to a specific state, or value, taken on by that rule. In Niklas’ (1994) hypothetical plant morphospace, the rules include the probability of branching and the angles at which the daughter branches emerge. Thus, each point in the landscape corresponds to a different morphology; i.e. the morphogenetic rules define a theoretical morphospace (Raup 1966; McGhee 1999, 2007). This is in contrast to genotypic landscapes, where several points in the landscape might correspond to the same morphology (e.g. see Green and Extavour 2012).
A theoretical morphospace becomes a fitness landscape if one can assign a fitness to each morphology (Fig. 1). In practice this is all but impossible to do, but it can be done in silico (see below), which permits useful discussion of how fitness landscapes might evolve.
|
The relationship between genotypic and morphogenetic fitness landscapes
At some level of causality the different states of each morphogenetic rule can be attributed to specific combination(s) of alleles. Alleles may constitute different nucleotide sequences for the same gene, either within an individual, or between individuals, or within or between populations, or between species, etc. Morphologically important allelic differences may be located in the coding regions, and/or in the control regions of a gene (e.g. the cis-regulatory nucleotide sequences), or in other parts of the gene (for example, at sites that control the processing of the mRNA for protein-coding genes), or in the genes for microRNAs that may also regulate a gene’s expression, etc.
The relationship between genetic change and morphological change is complex, not only because there are many genes involved directly and indirectly with morphogenesis, but because there is a hierarchy of processes that lead from individual alleles to specific states of given morphogenetic rule (Fig. 1). For example, it is becoming apparent that ‘morphogenetic’ genes are organised into gene-networks, which in turn control morphogenesis (Carroll et al. 2001; Davidson 2006). Thus, changes in morphology may result from: (1) the rewiring of specific networks, which may be reflected in changes in the nucleotides of the cis-regulatory elements; (2) how different networks are linked, which may be reflected at the allelic-level in changes in the nucleotide sequences of the amino acids that bind the regulatory elements of genes in other networks, or changes in the nucleotide sequences of the binding sites that those amino acids bind; and/or (3) the order in which the networks are activated, which may be controlled by the relative rates at which the cellular precursors of specific tissues or structures develop, which in turn are controlled by changes in their regulatory networks, or even by house-keeping genes such as the cell-cycle genes that control how quickly cells proliferate, etc.
It is well beyond the scope of this paper to attempt to resolve the complex and still relatively poorly understood relationships between genotypic changes and morphogenesis. Nonetheless, in some cases it has been possible to use our genetic understanding of morphogenesis to derive morphogenetic rules. For example, Salazar-Ciudad and Jernvall (2010) have developed a genetically informed model of tooth development that explicitly incorporates tissue mechanics (including cell adhesion, repulsion, etc. within the epithelium, and buoyancy and border growth in the mesenchyme) in a morphogenetic model of tooth development. Moreover, progress is being made in thinking about evolutionary innovation in a hierarchical framework (Erwin and Davidson 2009; Wagner 2011).
However, for the most part, the morphogenetic rules used to define theoretical morphospaces to date are not tied explicitly to the underlying genetics. Thus, we do not know yet whether there is a smooth mapping between small changes in the genotype and the resulting morphologies. That is, it is possible that small changes in genotype might translate into large jumps in a theoretical morphospace space. And we certainly have examples of small changes in genotype that lead to large changes in morphology (for example, homeotic mutations, or large-effect quantitative trait loci [QTLs]). If small changes in developmental genotype typically lead to large changes in phenotype, then the distances portrayed in a genetically uniformed morphogenetic morphospace will not correspond to the distances in the underlying genotypic space. Fortunately, our ignorance of how genotypic variation translates into phenotypic variation does not impinge on how morphogenetic fitness landscapes themselves evolve (the focus of this paper), but obviously impinges greatly on how easily lineages are able to explore those morphogenetic fitness landscapes (which is beyond the scope of this paper).
Fitnesses and the number of peaks in morphogenetic fitness landscapes
Fitnesses
Given a set of environmental conditions (E), and a set of k tasks (tk) that need to be performed in order for an organism to pass its genes on to the next generation, the morphology (M) of the organism will have a relative fitness (F), the relative likelihood that that morphology (and any concomitant behaviours, etc.) will pass its genes on to the next generation:

In practice it is difficult, probably impossible, to compute fitnesses for a given set of morphologies, let alone all conceivable morphologies. Nonetheless, it seems reasonable to assume that different morphologies will generally have different fitnesses in a given environment, and this is certainly the case in simulations (e.g. see Niklas 1994).
Number of peaks
For a set of i morphogenetic rules each with j states (mi,j), in an environment (E) where k tasks (tk) need to be performed, there will be a number, 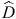 , of local fitness ‘highs’ or peaks, each of which corresponds to a locally optimal morphology:
, of local fitness ‘highs’ or peaks, each of which corresponds to a locally optimal morphology:

As with the calculation of fitness values for specific morphologies, generally speaking it will be difficult or impossible to calculate the number of peaks for a given theoretical morphospace given any specific configuration of the biotic and abiotic environments (but see below). However, there will be an expected number of peaks, nonetheless.
Eqn (2) implicitly captures the fact that the position of the peaks, i.e. the morphologies expected under Darwin’s theory of evolution, are a function of the morphogenetic rules (mi,j), conditional on the tasks the organism needs to perform to pass its genes on to future generations (tk), and the environment (E), both the biotic and abiotic.
The meaning of the peaks
Given that the peaks in a fitness landscape correspond to the morphological solutions that best satisfy the selective pressures that the organisms must satisfy to pass their genes on to future generations, a peak represents a best ‘engineering’ solution to the problems engendered by conditions of life for the group characterised by a specific set of morphogenetic rules. In this sense, each peak can be viewed as an ecomorph.
What can be done with morphogenetic fitness landscapes?
Despite the difficulty in calculating fitnesses for specific morphologies and estimating the expected number of peaks in a given fitness landscape, we can still determine how the location and number of peaks might change as the controlling variables – the morphogenetic rules, the environment and the number (and nature) of tasks that need to be performed – evolve. That is, we can ask in what ways can and do morphogenetic fitness landscapes evolve? This question is distinct from the question of how evolution proceeds on fitness landscapes (e.g. see Rice 2004; Gavrilets 2004), i.e. how fitness landscapes are explored, a topic that has attracted much more attention than how the landscapes themselves evolve.
The evolution of fitness landscapes
A fitness landscape can evolve in one of four fundamental ways: (1) it may change its roughness, the density of peaks on its (hyper)surface; (2) it may change its dimension, by changing the number of morphogenetic rules; (3) it may change its size, by changing the number of states that one or more of those morphogenetic rules can take; or (4) the peaks may simply shift their positions, leaving the roughness, dimension and size unchanged. Each of these is considered below.
Type 1 innovation: changing the roughness of a landscape
What determines the roughness of a fitness landscape?
I use the term roughness here to refer to the density of local optima on a landscape. If the landscape does not change in size, then this is a direct measure of the total number of peaks in the landscape (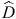 ). Others (e.g. Kauffman 1993) have used the term ‘ruggedness’ (or ‘smoothness’ for simple landscapes) for the same concept, but it is harder to make a verb of ruggedness so I use the term ‘roughness’ instead).
). Others (e.g. Kauffman 1993) have used the term ‘ruggedness’ (or ‘smoothness’ for simple landscapes) for the same concept, but it is harder to make a verb of ruggedness so I use the term ‘roughness’ instead).
Most workers simply assume a roughness, concentrating on how a fixed landscape is explored by evolving populations. But some have been concerned with what determines the roughness of the landscape itself. For example, Kauffman’s (1993) NK-model provides a way of tuning the roughness of a fitness landscape. In his model, N is the number of genes (typically each has just two states, or alleles), and K refers to the number of interactions between those genes. For K = 0 there are no interactions and the corresponding genotypic fitness landscape has just one peak (the landscape is very smooth). With maximal interactions, where each gene interacts with all other genes, K = (N – 1), the landscape is maximally rough, or rugged, due to fitness trade-offs between the interacting genes.
As discussed above, genotypic fitness landscapes are difficult to interpret morphologically, and the ability to meaningfully assign a value of K to a set of genes is particularly difficult, especially from a morphological standpoint. In addition, models like the NK-model do not explicitly incorporate the phenotype into the calculation of fitness or in the determination of the roughness of the fitness landscape. Thus, the limitations of genotypic fitness landscapes stem not only from the complexity of genetic interactions, but also from their inability to explicitly engage the particulars of the phenotype (and the environment) in the calculation of the fitnesses.
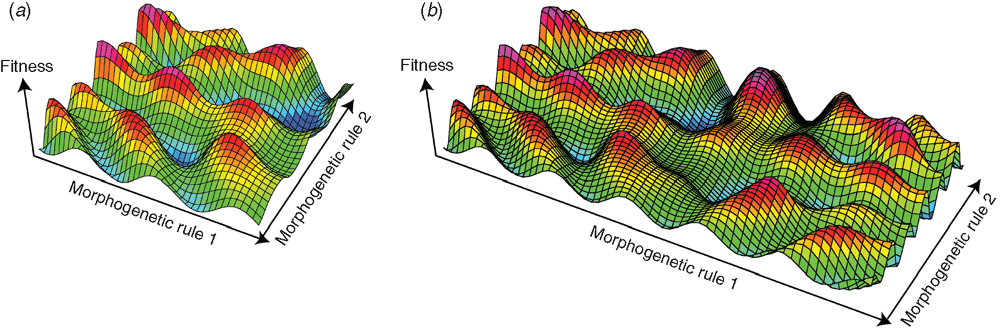
Nonetheless, the effect of trade-offs in roughening genic fitness landscapes is the same in morphogenetic fitness landscapes. For example, Niklas (1994, 1997, 2004), using a six-dimensional morphogenetic fitness landscape for the gross-level morphology of plants, shows that the roughness of his landscape is controlled by the number of interacting tasks the plants need to perform to pass their genes onto the next generation (rather than the degree of interaction between the genes, as in the case of Kauffman’s genotypic fitness landscapes). This insight was made possible because Niklas was able to evaluate the fitness of his computer-generated plants based on quantitative measures of each plant’s ability to perform explicit ecological tasks (tk), specifically how many seeds each could produce (and how well they could disperse), how effectively each could harvest light, avoid mechanical breakage of their branches, and avoid desiccation through minimising its surface area. More specifically, the roughness of the landscape stems from trade-offs associated with having to maximise the performance of all required tasks simultaneously. I return to this in more detail below, but first the central importance of trade-offs needs to be emphasised.
The Principle of Frustration
This principle (Marshall 1995, 2003, 2006) captures the empirical observation that the solutions needed to satisfy each of the different needs of an organism will often be in (partial) conflict with each other, so that the overall optimal design for an organism will rarely be optimal for any of the specific tasks it needs to perform (i.e. there will almost always be trade-offs). A good solution for meeting one need will typically (partially) ‘frustrate’ the ability to find a good solution for some other need. This is a phenotypic equivalent of Kauffman’s NK model, and I have taken the term ‘frustration’ from his analogy with spin glasses.
I have highlighted the importance of trade-offs when considering the fitness of an entire organism because I believe it is crucial to understanding the origins especially of disparity (see below, as well as Marshall 1995, 2003, 2006).
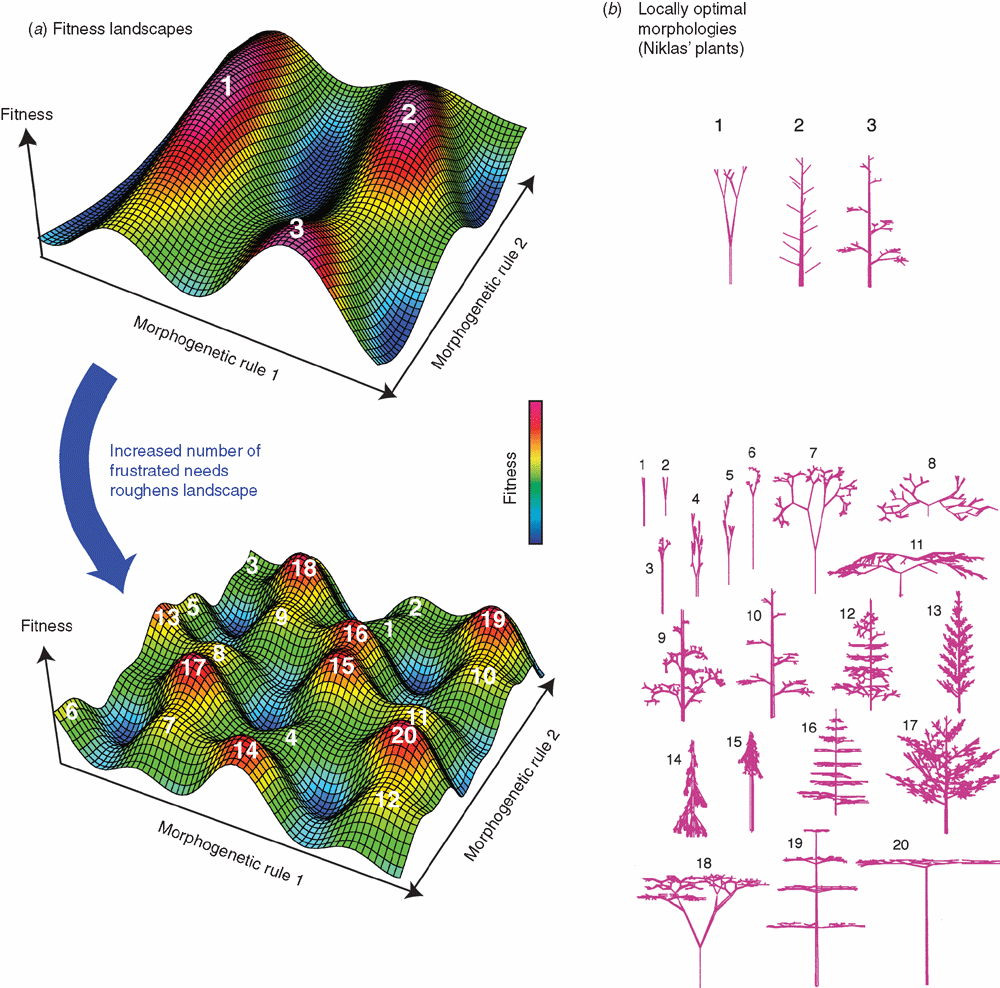
Usually, trade-offs come to the fore in discussions of specific functions, often as one of the components of an explanation for why a specific functional system in an organism does not have a fully optimal design, or performance, from a biomechanical point of view. Niklas’ computer simulations show the importance of the principle of frustration in shaping the overall morphology of organisms. When Niklas selected for just one task, the number of local optima (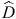 ) in his plant morphogenetic fitness landscape were few, typically 1–3. However, as he increased the number of tasks that needed to be performed, frustration set in, and both the number of local-optima increased, as did the average complexity (disparity) of those locally optimal solutions (Fig. 2).
) in his plant morphogenetic fitness landscape were few, typically 1–3. However, as he increased the number of tasks that needed to be performed, frustration set in, and both the number of local-optima increased, as did the average complexity (disparity) of those locally optimal solutions (Fig. 2).
|
Simply put, an optimal solution for one need typically compromises the ability of an organism to perform some other need, a principle well understood by engineers of complex systems (Csete and Doyle 2002). It is this fact that leads to a multitude of locally optimal morphologies. In the case of Niklas’ plants, maximising reproductive success requires maximising the number of branches (actually branch-tips, where the seeds form) and the heights of those branch tips to maximise dispersal. Maximising light harvesting, while also requiring many branches, requires the higher branches to be smaller to minimise overshadowing and the branches need to be oriented horizontally, rather than vertically, to maximise light interception. Minimising the risk of breaking branches means limiting horizontal branch length, which is in conflict with needs of light interception. And finally, minimising surface area means limiting branch length, regardless of orientation, which compromises both reproductive success and light interception. Some of the trade-offs are in branch length, some are spatial (the need for horizontal versus vertical branches), others a combination of both. The key point is that when all tasks need to be performed the trade-offs combine to produce a wide range of local optima, given the rules for making the plants.
Thus, it is frustration that leads to an increase in roughness of a fitness landscape, the number of local optima, as the number of needs increase. While the number of local optima in a fitness landscape will depend on the specific morphogenetic system (e.g. whether we are dealing with plants, or animals, molluscs, etc.) and on the range of environments, E, in which the clade finds itself, the roughness of the landscape will also depend on the number of tasks (k in tk) that need to be performed. Following Niklas, f(k) will be larger as we increase the value of k. This is a very powerful result. It says that regardless of the morphogenetic rules, and even though we usually cannot compute fitnesses for morphologies in theoretical morphospaces, we expect the number of optimal peaks and the disparity of a clade to increase as the number of tasks that need to be performed by the clade increases.
How many peaks should there be?
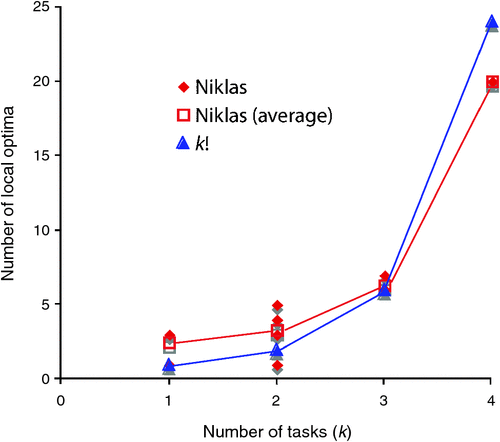
The number of peaks will most likely depend on the morphogenetic system, the degree of frustration, and the manner in which the frustration is expressed (for example, with Niklas’ plants sometimes the frustration is in terms of the number of branches, in other cases it is simply in their orientation). Nonetheless, generally different morphologies will have different fitness values for different specific tasks. For example, again turning to Niklas’ plant simulations, some plants have very low surface areas (minimising the loss of water at the expense of seed production and photosynthetic capacity), while others have a large number of branches (maximising photosynthetic capacity and seed production, thus paying a high cost in water loss and the likelihood of losing some of their branches). For each locally optimal design, it is possible to rank each of the fitness factors according to their relative importance to the overall fitness, and thus there are k! ways of ordering the importance of the k tasks (ignoring ties). Hence the number of peaks in the landscape should follow:

Niklas’ computer simulations are compatible with this hypothesis (Fig. 3).
|
Example of the roughening of a fitness landscape: the Cambrian explosion
For most clades, for most of their history, I suspect their fitness landscapes neither roughen (nor smooth) appreciably. Typically, the fundamental needs of organisms are set and their ecological roles relatively fixed. Thus, the number (k) of tasks they need to perform to satisfy those needs is largely invariant, and so the density of peaks, the number of local optima, is largely unchanging. That is, I suspect roughening is not a common mode of evolution.
However, there was a specific time in the history of animal life when I believe roughening played a major role in driving disparity, and that is during the Cambrian explosion of animals (Marshall 2003, 2006). The phylogenetic distribution of key developmental genes in living species suggests that the basic developmental toolkit for animals was already in place before the radiation of at least the bilaterian phyla (Carroll et al. 2001; Davidson and Erwin 2006; Marshall 2006; Erwin and Davidson 2009; Davidson 2010; Marshall and Valentine 2010; Erwin and Valentine 2013), certainly before the end of the Ediacaran. This developmental system appears to be combinatorial in nature; that is, different morphologies seem to stem from changes in the way the genes are wired together. Davidson and Erwin (2006) elaborate on this basic idea by identifying conserved kernels that define superphylum- and phylum-level characteristics, and then different ‘plug-in’ gene circuits and different inputs and outputs that control the differences between classes, orders, etc.). Thus, at some level of generality, there is a universal developmental toolkit held in common by all phyla, and it appears that modification of that toolkit may have been responsible for the major differences between the phyla. That is to say, it seems reasonable to assume that this developmental toolkit translates into a set of morphogenetic rules that unites all, or most, animals, and thus it is reasonable to place the phyla in a single theoretical morphospace, although this space has yet to be explicitly defined.
Most interestingly, it appears that animals of the Ediacaran, which immediately predates the Cambrian explosion, had a dearth of macroscopic sensory organs (compound eyes, antennae, setae, etc.) and they also lacked macroscopic organs of direct interaction with either organisms of similar size or the environment (there are no legs, swimming appendages, claws, etc.). Further, they show no signs of predation, except for rare bore holes in the first skeletonised taxon, Cloudina, from the latest Ediacaran (Hua et al. 2003). Thus, it indeed appears to have been the garden of Ediacara (McMenamin 2000) – macroscopic adult-body/adult-body interactions were minimal – nature was not yet red in tooth and claw.
With the advent of ecological interactions between macroscopic adults (especially interactions associated with predation), the number of tasks each organism needed to meet must have increased markedly: now there was a range of predators to contend with, which led to a variety of ways of avoiding them, which led to further specialised ways of predation, and so began the morphological arms-race. Even with no changes in the bilaterian developmental system as it existed by the end of the Ediacaran, the diversity and disparity of animals should have risen sharply, as the fitness landscape roughened with the increasing levels of frustration.
I offer this as a null hypothesis explanation for the Cambrian explosion. However, it is quite likely that the size of the fitness landscape (for example through gene duplications), and the dimension of the landscape increased as well (see below), but if we could replay the history of life, but limit mutational events to simply the rewiring of existing gene regulatory networks, I suspect we still would have seen a spectacular explosion of new and complex animal forms. That is, I suspect that roughening was a major component of the Cambrian explosion (Marshall 2003, 2006).
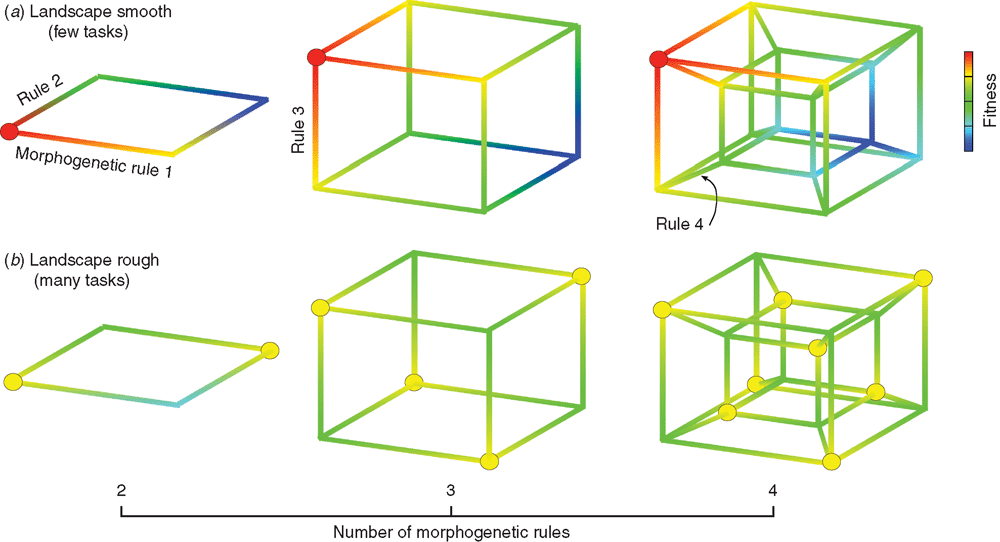
Type 2 innovation: changing the dimensionality of a landscape
In the cartoons of fitness landscapes presented above each has just two morphogenetic rules, which I have used to define the x–y plane. In reality, organisms have a larger number of morphogenetic rules, and even ‘simple’ theoretical morphospaces typically have more than two rules (e.g. Niklas’ plant morphospace is 6-dimensional, Raup’s molluscan morphospace has 3 parameters, while Wolfram’s (2002) extension of Raup’s space has 5 morphogenetic rules). Clearly, one of the major features of evolution is the evolution of new developmental programs that offer new morphogenetic potentials.
The development of a new morphogenetic potential in a morphogenetic fitness landscape is equivalent to adding a new gene in a genotypic fitness landscape; both increase the dimensionality of the space by one (Fig. 4). Hendry et al. (2012) also consider cases where the dimensionality of a fitness landscape relevant to a particular selection pressure may increase, although their discussion does not involve the evolution of new dimensions per se.
Examples
Without a detailed knowledge of the genetic basis of morphogenesis it is difficult to provide fully substantiated examples of the evolution of new morphogenetic rules, or capacities. Nonetheless, I suspect this mode of evolution operates whenever a new morphogenetic axis (dimension) is required to describe new species within a clade. Thus, the origin of coiling in nautiloid cephalopods, or the origin of jaws in fish, represent examples of this mode of evolution.
Speculation: on the extinction of the trilobites
It is interesting to speculate on whether a clade’s long-term survivorship might depend on its ability to ‘remake’ itself by adding dimensions to its theoretical morphospace. For example, trilobites are the only major clade of arthropod that never developed the capacity to either fuse their appendages (e.g. a mechanism employed by many insect groups to form their feeding organs), or modify their appendages’ distal ends (e.g. as commonly employed by crustaceans for locomotion among other functions, or make jaws as seen in the chelicerates). This perhaps left the trilobites in a lower-dimension morphospace compared with other arthropods, and certainly means they were all restricted in the size and nature of the food that they could ingest, and also, compared with other arthropod groups, limited their capacity to move in the water column and either evade or defend themselves against predators. Thus, perhaps, at some deep level, the failure of trilobites to increase the dimensionality of their morphospace was at the root of their demise.
Type 3 innovation: changing the size of a landscape
The third way a fitness landscape can evolve is by increasing the size of one or more of the existing dimensions, by increasing the number of character states that a given morphogenetic rule can take (Fig. 5).
Example: flower evolution
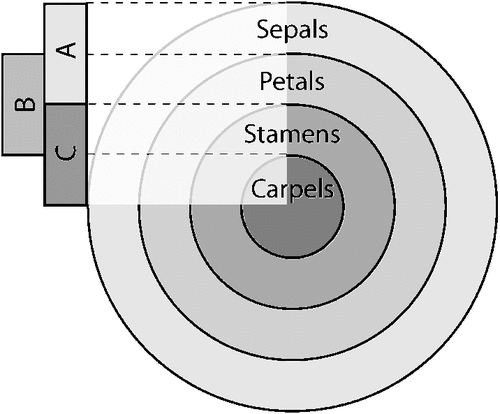
Providing detailed examples of this mode of morphological innovation is difficult due to our lack of understanding of the details of the genetic underpinnings of the development of most morphological characters. Nonetheless, it is likely that changing the number of possible character states for a character may often involve gene duplications through processes such as subfunctionalisation (Lynch and Force 2000). For example, it is likely that some of the diversification of flowers in angiosperms was enabled by duplications of key developmental genes. In Arabidopsis concentric and overlapping domains of gene expression determine the basic structure of the flower; expression of A genes alone produce sepals, coexpression of A and B genes lead to petals, coexpression of B and C genes leads to stamens, while expression of C alone leads to the centrally located carpels (Fig. 6). If the B-class genes are knocked out, then the flower is made of two circlets of sepals that surround two circlets of carpels. As more angiosperms are studied, it is becoming apparent that this basic system is not conserved, and that there have been duplications of at least some of these genes, especially the B-class genes, that have played a role in the evolution of novel floral structures (Litt and Kramer 2010). Thus, it appears that the size of the morphogenetic axes for floral development has increased as pollinators (insects, birds, etc.) that use petals as cues for pollination fixed modified duplicates of the ancestral genes.
|
Caveat
Without knowing the genetic basis of morphogenesis, it is hard to distinguish between a landscape that is increasing in size from one that is of constant size, but appears to be growing as more and more peaks are successfully explored. It matters how well, and how quickly, evolution is able to explore fitness landscapes.
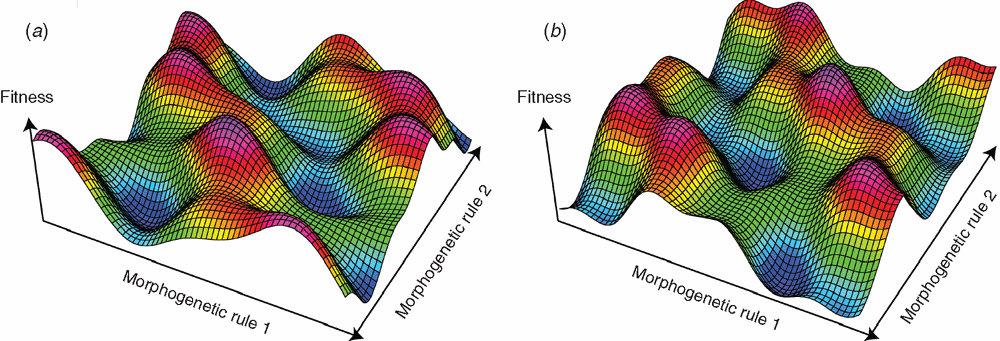
Type 4 innovation: changing the position of the peaks in a landscape
Finally, the roughness, dimensionality, and size of the landscape may remain constant, but the position of the peaks may shift (Fig. 7) (Simpson 1944; Arnold et al. 2001; McGhee 2007). Here the primary driver of morphological change is environmental change (given that changes in developmental potential only change the dimension or size of a landscape). The environmental change may be biotic or abiotic or both.
Note here the importance of distinguishing between the initiators of the morphological change, and how a specific morphological change is actually made manifest. At a fundamental level, all morphological change is achieved through changes in development. This is reflected within the framework of fitness landscapes by the simple fact that morphological change is achieved by moving on the landscape, that is by changing one’s specific position within the morphogenetic (and thus developmental) space. But, in Type 4 morphological change/innovation, environmental change is the primary driver, which alters the positions of the peaks, which in turn leads to movement in the morphospace. While this movement in morphospace is achieved through changes in development, for example through changing the patterns of expression of key developmental genes, as appears to be the case in the vertebrate fin to limb transition (Schneider and Shubin 2013), the fundamental developmental system remains unchanged.
I suspect that this is the most common form of morphological change. New species constantly appear in the fossil record that are immediately assignable to existing genera, or families; they do not posses neomorphs or unusual morphologies, and so do not exhibit new morphogenetic potentials. Support for this argument comes from Wagner’s (2000) demonstration that as clades age they add progressively fewer new character states. This progressive exhaustion of morphologic character states strongly suggests that as clades evolve they tend not to increase the dimension or size of their morphospaces. But of course new morphotypes are seen (reflected in the description of new characters), and so typically there are also episodes of ‘character release’ with an increase in the number of potentially varying characters (e.g. see Wagner et al. 2006).
Stasis and when environmental change might lead to large morphological change
The Principle of Frustration most likely retards the magnitude of morphological change with minor environmental change. This is because while environmental change might favour a change in some characters, trade-offs with other needs will offset any fitness advantages of those character changes. For example, in Niklas’ simulations, decreased light might require increased branch length, but this is offset by increased likelihood of desiccation and breaking branches. Thus, most of the time, it seems likely that environmental change will typically only result in prosaic morphological change, if it leads to any change at all. In fact, the existence of functional trade-offs may very well explain the numerous examples of stasis seen in the fossil record (Gould and Eldredge 1993; Hunt 2007).
However, large morphological change is expected when there is a major environmental change, especially if there is a shift in the medium in which the organism lives; for example, if members of a clade move from marine or fresh water habitats to terrestrial habitats, or vice versa, or from terrestrial habitats to aerial habitats (as was the case in the evolution of birds, bats and pterosaurs), or from the surface of the substrate to an infaunal mode of living (for example, with some bivalves and echinoids), or from the surface of the substrate into the water column (e.g. pelagic trilobites), or when new habitats emerge, whether it be nooks and crannies in coral reefs (which provide shelter for many species), or places for epiphytic growth in trees.
While it is tempting to attribute the morphological changes associated with a change in the medium in which the animal lives to new genetic potentials, detailed analysis of the anatomy of taxa that had made these transitions shows that this is typically not the case. For example, in the case of vertebrate evolution, while there is a great deal of morphological change associated with the origin of whales, ichthyosaurs and plesiosaurs, or with the evolution of bats, birds and pterosaurs, for the most part there are no neomorphs associated with these transitions; that is, there are no obvious changes in the underlying developmental system. In the case of terrestrial to aquatic and marine transitions, the overriding importance of drag in water compared with air, and the corresponding decrease in the importance of gravity, leads to dramatic changes in morphology, with the evolution of fusiform body shape, a decrease in the complexity of the vertebral column, often the reduction of the hind limbs, almost always a loss of differentiation of the shapes of the bones of the limbs, the posterior movement of the external nares, etc. And in the case of the evolution of birds from theropod dinosaurs, feathers, hollow bones, pneumatic lungs, etc. were already in place. In all these instances, the initiator of evolutionary innovation was primarily environmental, not developmental, even though all require developmental change (see above).
Example: evolutionary arms races – the surfing of coevolving fitness landscapes
In evolutionary escalation (Vermeij 1987) an evolutionary innovation in one clade changes the position(s) of fitness peaks in the fitness landscape of another clade, which in turn changes the position of the fitness peaks in the first clades’ landscape, which, if the escalation persists, leads to further changes in the position of the fitness peaks in each of the coevolving clades’ landscapes (Brodie and Ridenhour 2003; Brodie et al. 2005; Thompson 2005; McGhee 2007; Calsbeek et al. 2012). An excellent example of this sort of coevolution is the increased ability of the thiarid gastropods in Lake Tanganyika to resist the shell crushing and peeling capability of the lake potamonautid crabs with their correspondingly enlarged chelae (West et al. 1991; West and Cohen 1996). Thus coevolutionary escalation results in the codeformation of the fitness landscapes of two or more clades. Both groups successfully surf their respective fitness landscapes as the peaks move, a type of evolutionary change that can be couched in terms of the Red Queen hypothesis (e.g. see McGhee 2007).
In most instances escalatory induced change will initially be expressed as the shifting peaks in an otherwise fixed landscape, but eventually the escalatory selective pressure might lead to the fixation of new genetic potentials that will either increase the size, dimension, or both, of the fitness landscape. Long-term escalatory selective pressures may be one of the dominant drivers of the increase in both the size and dimensionality of fitness landscapes.
In the case of evolutionary escalation, the primary driver of morphological change is a change in the biotic environment.
Example: sticklebacks
Numerous freshwater invasions by three-spine sticklebacks from the marine realm have led to stereotyped morphological changes, including armour reduction and change in body shape (Bell and Foster 1994; McKinnon and Rundle 2002). In the marine setting there is one fitness peak, in freshwater another. Thus, from the point of view of the sticklebacks their local fitness peak had moved as they changed environments. However, the populations did not track a moving peak. Rather, in moving to freshwater the relative fitness high that corresponds to their marine morphology was reduced with respect to a new relative fitness high that corresponds to their freshwater morphology. In the process of changing their environment the sticklebacks were dumped into a fitness low with respect to their armour and body shape, but they quickly climbed a new fitness high that appears to have been relatively accessible (Chan et al. 2010; Jones et al. 2012).
The inference that sticklebacks repeatedly climbed a new fitness peak in the freshwater realm has been confirmed in a remarkable palaeontological setting, in a 10-million-year-old glacial-fed lake. Using the fact that annual layers (varves) can be seen in the lake sediments, Bell et al. (2006) were able to measure phenotypic change on ecological timescales, and Hunt et al. (2008) showed that three different components of body armor reduction measured every 250 generations follow the paths expected for a population climbing a new fitness peak. That is, the trajectories of morphological change follow the expectations of an Orstein–Uhlenbeck process.
Taxa need not pass through fitness valleys to shift peaks
A criticism of the idea of isolated fitness peaks comes from the difficulty in explaining how species cross fitness valleys to get from one peak to another (e.g. Gavrilets 2004, p. 114). However, with evolutionary escalation (see above) lineages simply track moving peaks, an idea well elaborated by Simpson (1944) (see also McGhee 2007). In the case of the stickleback populations that moved from the sea to freshwater habitats the populations neither tracked their fitness peak nor traversed a fitness valley – they simply found themselves in a relative fitness low with respect to their armour and body shape (this component of their fitness landscape collapsed under their very fins) and they were able to climb to a fitter morphology.
Similarly, Estes and Arnold (2007) have argued that the temporal patterns of anagenesis seen in the fossil record (Gingerich 1983) can be accounted for by lineages simply tracking the movement of their fitness peaks over various times scales, for just a few generations to tens of millions of generations.
Thus, once one recognises that fitness landscapes themselves can evolve, there is no longer the need to invoke the idea that populations cross fitness valleys to explain the distributions of different lineages on different fitness peaks.
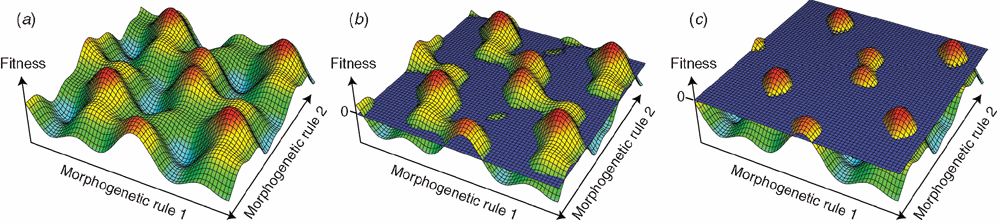
Diagramming non-specific (generalised) evolutionary escalation – rising ‘sea-levels’ on fitness landscapes
In the Lake Tanganyikan gastropod–crab example of evolutionary escalation discussed above, there was a very specific coevolution between the crabs’ ability to breach the snails’ shell, and the snails’ ability to resist such invasions of privacy. That is, there was a very specific coevolutionary process between the two clades. However, it is quite likely that during the course of the Phanerozoic many ecosystems became progressively more escalated as each of their constituent clades adjusted to innovations of other clades (Vermeij 1987). Thus, for taxa that interact with many other clades, avoiding predators, securing food, providing adequate protection for offspring, etc., may have become progressively more challenging.
This more generalised evolutionary escalation, to the extent that it occurs, may lead to the deformation of a clade’s landscape (the shifting of the peaks), but it is also possible that frustration (functional trade-offs) leaves no way out for many species (see above) – the peaks stay in place, but become progressively less optimal. Thus, non-specific (or generalised) evolutionary escalation can be diagrammed by introducing a surface of zero fitness (a ‘sea-level’) onto the fitness landscape (Fig. 8), and the escalation may be diagrammed by increasing in the height of the ‘sea-level’ on the landscape, which may in turn genuinely isolate peaks. Note, however, that it is unlikely that the plane of zero fitness will actually be flat.
A palaeontological example that documents local evolutionary escalation comes from McCune’s (1990) work on the colonisation of an expanding lake by fish in the Semionotus complex in the Early Jurassic. Once again taking advantage of annual sedimentary layers (varves) in a fossil lake she has shown using 1700 specimens collected from 21 000 years of sedimentary layers that individuals with anomalous variation in dorsal ridge scales are concentrated in the early phase of lake formation, when presumably the early colonisation was associated with relaxed selection.
Diagramming a catastrophic perturbation – tsunami!
Consistent with use of a rising sea level to diagram non-specific escalation, a catastrophic perturbation, for example, the impact of the end-Cretaceous bolide, would be equivalent to the flooding of the landscape with a tsunami.
Discussion
Are phenotypic fitness peaks really isolated?
Many have noted that while the depiction of fitness landscapes as three-dimensional topographic surfaces provides a powerful heuristic for thinking about evolution, the low dimensionality of such cartoons may be seriously misleading. For example, in the figures presented above, all the fitness peaks are isolated from one another. However, the peaks in real fitness landscapes may be connected by ridges of high relative fitness. For example, Gavrilets (2004) argues that in highly dimensional fitness landscapes (typical of genotypic landscapes) the peaks are, by mathematical necessity, connected via ‘ridges’ of a similar fitness to the peaks themselves. Further, Gavrilets (2004) argues that the connection of the peaks via these nearly neutral ridges means that populations need never cross fitness valleys, which neatly solves the conundrum of how populations cross fitness valleys.
A full discussion of the reasons for believing that there are isolated fitness peaks in morphogenetic fitness landscapes is beyond the scope of this paper. However, there is a general sense that phenotypic fitness landscapes have a lower dimensionality than genotypic fitness landscapes (Wade 2012), or at least effectively have a lower dimensionality (Calcott 2008). Certainly, the dimensionality of the morphogenetic fitness landscapes described above are much lower than the genotypic fitness landscapes discussed by Gavrilets (2004). In addition, as discussed above, the possibility that fitness peaks can move suggests that populations might track moving peaks, or, with a change in the environment, suddenly find themselves in a fitness low close to a new fitness high. That is, the existence of isolated fitness peaks does not require that populations pass through fitness lows to evolve new morphologies.
Finally, there is empirical evidence for the existence of separate morphological fitness peaks; for example, in body size for Cenozoic mammals (Alroy 1998), gastropod shells (Wagner and Erwin 2006), vultures (Hertel 1994), large mammalian carnivores (Van Valkenburgh 1995), as well as within subgroups of these mammals, including within the canids (Slater et al. 2009) and bone-cracking hypercarnivores (Tseng 2013).
Limitations on morphological form need not be due to developmental constraint
The term ‘developmental constraint’ evokes the sense that if a developmental constraint were removed then new morphologies could be produced. Thus, it might be assumed that the inability of a clade to evolve a morphology that is fully optimal for all the needs it must meet to propagate itself is a consequence of developmental constraints. However, this need not be the case. The principle of frustration, the fact that there will almost always be functional trade-offs, is independent of the developmental system. The reason is that the functional trade-offs are the result of the engineering conflicts that arise when trying to perform multiple functions; these constraints are at the phenotypic, not genotypic, level.
Developmental rules – constraint or opportunity?
Without morphogenetic rules, there is no morphology. With a given set of morphogenetic rules there is morphology, and evolution must maximise fitness using those morphogenetic rules. These rules thus represent opportunity, but may also be viewed as constraint (for example, in Niklas’ system, branches can, at most, bifurcate). Thus, morphogenetic rules are both generative (we have morphology) and limiting. And the limitations are themselves organising, for an organism has to use the morphogenetic tools available to it to meet its ecological needs given the limitations of its morphogenetic rules. Thus, for example, straight nautiloid cephalopods organised around the engineering challenge of maintaining their orientation in the water column as they grew, and the developmental constraint of being unable to coil, by developing different ways of depositing material within their bodies, for example in their chambers, their siphuncle, etc. Thus, from a morphological point of view the notion of a developmental constraint is hard to separate from the ecology and functional needs of the organism (Marshall 2010).
The term developmental constraint also has several other meanings, and I don’t want to downplay these here. For example, Niklas (1997) defines developmental constraint (operationally) as the inability of a developmental system to achieve certain sets of parameter values implicit to a set of developmental rules (some values of j cannot be expressed in mi,j). In this instance, interestingly, developmental constraint increases the number of peaks in the landscape.
Relationship to Darwin’s theory of evolution
This framework meshes perfectly with Darwin’s theory of evolution. In simplest terms, Darwin’s theory is a two-step process, variation followed by selection, or, to recast it, the control (Van Valen 1973, 1974) or filtering (Marshall 1995) of development by ecology. Under the schema of fitness landscapes the variation/development phase of the Darwinian ‘two-step’ is captured by movement in the theoretical morphospace, while the selection/ecological phase is captured by the fitness component of the landscape, given an environment, or range of environments (both biotic and abiotic).
What proportion of peaks in a fitness landscape are occupied?
A key question that arises from conceptualising morphological innovation from the perspective of fitness landscapes is what proportion of fitness peaks on a landscape are occupied at any given time? Are most peaks occupied? If not, as appears to be the case for bone-cracking carnivores (Tseng 2013), is it because evolution is simply ineffective in finding all the peaks in a landscape, or is it because landscapes evolve faster than the rate at which evolution can explore them? Or does the truth lie somewhere in between?
If evolution typically explores landscapes rapidly compared with the rate of change of the fitness landscape, then morphological innovation is largely controlled by the processes that cause fitness landscapes to change their topology. On the other hand if the rate of evolution is slow compared with the rate of evolution of the landscape, then the process of exploration becomes a significant factor in determining the morphological innovations we see in the fossil and living biotas. Providing answers to these difficult questions is beyond the scope of this paper. Nonetheless, some simple observations are offered as a way of beginning to address these questions.
The exploration of fitness landscapes: E ≈ (MC)2
As noted above, Darwinian evolution is a two-step process, variation followed by selection. This can be recast in the context of Markov chain Monte Carlo (MCMC, or [MC]2) techniques (e.g. Harper 2009). These are typically used when trying to find maxima of complex probability density functions, for example when trying to find the most likely phylogenetic tree in a Bayesian analysis (Ronquist and Huelsenbeck 2003; Ronquist et al. 2012). Typically, in each step of an (MC)2 algorithm a new state is proposed through the application of a jumping rule, which determines in what direction, and how far, the next putative step (jump) in the exploration of the probability density distribution will be taken, followed by the application of an acceptance rule that determines whether or not the new state is accepted, or rejected. If the new state is accepted, the next round of the simulation starts from that point, while if it is rejected the process starts again from the initial point. In evolutionary terms, the jumping rule is analogous to variation, where the proposed new step might be the new mean of a character in the next generation, while the acceptance rule, is equivalent to the process of natural selection, where the new variant is accepted (there is directional selection), or not (selection is stabilising).
Thus, Darwinian evolution (E) is analogous to the operation of a Markov chain Monte Carlo algorithm (MC2), where the probability density function to be explored is the topology of the fitness landscape, that is E ≈ (MC)2.
I use the ‘approximately equals’ symbol, because there are many differences in detail between the way (MC)2 is typically implemented and the way evolution operates. Perhaps the most important difference is that there are no populations in (MC)2 – each chain is analogous to the mean value of the phenotype of the population or species, but selective evolutionary change is typically driven by the differential survival of favoured individuals that differ from the mean phenotype. In addition, there is typically no speciation in (MC)2 (the number of chains is fixed), and in biology there is no equivalent of heated chains, where some chains are allowed to explore severely suboptimal paths.
Despite these and other differences, the reason I draw the analogy is simply to note that (MC)2 algorithms appear to be highly effective in finding optimal, or nearly optimal, peaks in highly complex probability density functions. In the case of phylogenetic analysis, in the order of millions of steps is often all that is needed to reach stationarity, for a chain to settle on a (presumably) optimal peak. In evolution each step in the analogous (MC)2 process is roughly equivalent to a generation. Thus, if exploring tree space is analogous to exploring fitness landscapes, then evolution should find the peaks on a fitness landscape in the order of millions of generations. If evolution is as efficient as, or more efficient than, our (MC)2 algorithms (as might be the case, given the variety of mechanisms for producing variation, from sorting through the different combinations of already existing alleles, to point mutations, recombination, gene conversion, gene duplication, cis-regulatory changes, as well as the fact that small genetic changes can have large effects, not to mention phenotypic plasticity and epigenetic effects (Gilbert and Epel 2009)), then evolution might be very effective at finding the peaks on fitness landscapes. Moreover, if a species has already found a fitness peak, which was then to move a short distance, the evolutionary process will find the new peak much more rapidly given that the population is already close to the new phenotypic optimum.
For many taxa, generation times are in the order of a year, and thus this back-of-the-envelope argument implies that morphological innovation should typically occur in less than a million years, a fact born out by the recognition that the morphological change between species often appears punctuated in the fossil record (Gould and Eldredge 1993).
In summary, given that Bayesian methods can find optimum trees among several possible trees that greatly exceed the sum of the number of vibrations performed by every atom in the known universe since the Big Bang (some 10110 vibrations), then it seems reasonable to posit that evolution is able find most of the optimal peaks in fitness landscapes on ecological to short geological timescales.
Niklas’ computer simulations mimic the Devonian plant radiation
The second observation relevant to the question of how effectively evolution is able to find the peaks in a fitness landscape is the simple fact that in Niklas’ computer simulation of gross plant morphologies (Fig. 2), Niklas is able to mimic, with some degree of fidelity, the plant fossil record as we observed it by about the end of the Devonian. With just four selective pressures, and six developmental rules, it appears, to first order, that Niklas has been able to mimic the evolution of land plants. Thus, it would appear that evolution is indeed able to find most of the fitness peaks available to it. Interestingly, this process appears to have taken in the order of 107 years.
Similarly, other adaptive radiations appear to have proceeded at about the same rate, from the Cambrian explosion, to the radiation of jawed fish in the Devonian, to the radiation of mammals in the Palaeocene and Eocene after the demise of the non-avian dinosaurs at the end of the Cretaceous. The fossil record suggests then that evolution is capable of exploring new fitness landscapes in the order of 107 years, or generations.
Future directions
Given the basic framework outlined above, several areas of future enquiry come to mind: (1) To what extent can our understanding of the genetic basis of morphogenesis be abstracted into theoretical morphospaces? To date, the most convincing example is Salazar-Ciudad and Jernvall’s (2010) genetically informed model of tooth development. (2) What are the relative frequencies of the different modes of fitness landscape evolution? (3) Is there a relationship between the modes of fitness landscape evolution, evolutionary novelty, rates of diversification, and overall diversity? If so, what are these relationships? (4) What are the implications for how rates of morphological evolution should be distributed? For example, Wagner (2012) suggests that morphological rate distributions should follow log-normal distributions rather than the gamma distributions thought to typify molecular characters. Does the framework presented here alter that prediction?
The search for evolutionary laws: beyond contingency
Gould (1980) outlined the promise of palaeobiology as a nomothetic discipline. In that paper, Gould described the difference between the nomothetic, the search of general laws or rules, and the idiographic, the detailed description of unique events, and argued for the importance and promise of discovering underlying rules and generalities in the forces that have shaped the history of life. Interestingly, by 1989, with the publication of Wonderful Life, Gould (1989) seemed to have settled on contingency as one of the most important determinants of evolutionary success. A generality of no generality; to my mind he effectively abandoned the nomothetic for the idiographic.
The framework developed here provides the means, in principle, to establish the balance between the idiographic and nomothetic in explaining the causes of morphological innovation. If landscapes only evolve slowly and evolutionary processes are indeed capable of solving the np-complete problem of effectively exploring fitness landscapes over geological timescales, then understanding the optimal morphologies and the morphogenetic rules for a given clade should enable a powerful predictive framework for understanding the patterns of morphological innovation we observe. On the other hand, if most fitness landscapes are constantly being deformed by the presence of a wide range of other species, then it is possible that it will be much harder to develop a nomothetic understanding for the history of morphological innovation.
As we work towards developing our understanding of the relative importance of nomothetic versus idiographic (and thus contingent) forces in shaping the history of life, I advocate that in our ignorance we are better served adopting a null hypothesis of nomothetism, rather than contingency. The world is sufficiently complex that if we don’t assume there are deep laws underlying the patterns of morphological innovation that we observe we are unlikely to discover them, even if in the end the scope of those laws is less universal than we might have initially hoped for.
Acknowledgements
Many contributed to this work, but I want to especially thank Richard Bambach, the graduate students in my graduate courses in Analytical Paleontology at Harvard University (particularly Woody Fisher and Jon Payne), as well as input and encouragement from David Roberts, Brett Calcott, and Gunther Wagner. Thanks also to the Editor, an anonymous reviewer, and a review by Peter Wagner for valuable suggestions for improvement.
References
Alroy, J. (1998). Cope’s Rule and the dynamics of body mass evolution in North American fossil mammals. Science 280, 731–734.| Cope’s Rule and the dynamics of body mass evolution in North American fossil mammals.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaK1cXjtVOkt74%3D&md5=96ff0eea3b122b057d5a68bb0e465459CAS | 9563948PubMed |
Arnold, S. J., Pfrender, M. E., and Jones, A. G. (2001). The adaptive landscape as a conceptual bridge between micro- and macroevolution. Genetica 112/113, 9–32.
| The adaptive landscape as a conceptual bridge between micro- and macroevolution.Crossref | GoogleScholarGoogle Scholar |
Bell, M. A., and Foster, S. A. (1994). ‘The Evolutionary Biology of the Threespine Stickleback.’ (Oxford University Press: Oxford.)
Bell, M. A., Travis, M. P., and Blouw, D. M. (2006). Inferring natural selection in a fossil threespine stickleback. Paleobiology 32, 562–577.
| Inferring natural selection in a fossil threespine stickleback.Crossref | GoogleScholarGoogle Scholar |
Brodie, E. D., and Ridenhour, B. J. (2003). Reciprocal selection at the phenotypic interface of coevolution. Integrative and Comparative Biology 43, 408–418.
| Reciprocal selection at the phenotypic interface of coevolution.Crossref | GoogleScholarGoogle Scholar | 21680449PubMed |
Brodie, E. D., Moore, A. J., and Janzen, F. J. (1995). Visualizing and quantifying natural selection. Trends in Ecology & Evolution 10, 313–318.
| Visualizing and quantifying natural selection.Crossref | GoogleScholarGoogle Scholar |
Brodie, E. D., Feldman, C. R., Hanifin, C. T., Motychak, J. E., Mulcahy, D. G., Williams, B. L., and Brodie, E. D. (2005). Parallel arms races between garter snakes and newts involving tetrodotoxin as the phenotypic interface of coevolution. Journal of Chemical Ecology 31, 343–356.
| Parallel arms races between garter snakes and newts involving tetrodotoxin as the phenotypic interface of coevolution.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXhvF2qs7g%3D&md5=2483be257bc14aad172f5d11bf162278CAS | 15856788PubMed |
Calcott, B. (2008). Assessing the fitness landscape revolution. Biology and Philosophy 23, 639–657.
| Assessing the fitness landscape revolution.Crossref | GoogleScholarGoogle Scholar |
Calsbeek, R., Gosden, T. P., Kuchta, S. R., and Svensson, E. I. (2012). Fluctuating selection and dynamic adaptive landscapes. In ‘The Adaptive Landscape in Evolutionary Biology’. (Eds E. I. Svensson and R. Calsbeek.) pp. 89–109. (Oxford University Press: Oxford.)
Carroll, S. B., Grenier, J. K., and Weatherbee, S. D. (2001). ‘From DNA to Diversity.’ (Blackwell Science: Oxford.)
Chan, Y. F., Marks, M. E., Jones, F. C., Villarreal, G., Shapiro, M. D., Brady, S. D., Southwick, A. M., Absher, D. M., Grimwood, J, Schmutz, J, Myers, R. M., Petrov, D, Jónsson, B, Schluter, D, Bell, M. A., and Kingsley, D. M. (2010). Adaptive evolution of pelvic reduction in sticklebacks by recurrent deletion of a Pitx1 enhancer. Science 327, 302–305.
| Adaptive evolution of pelvic reduction in sticklebacks by recurrent deletion of a Pitx1 enhancer.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXktlWktg%3D%3D&md5=c7d0cd8ef789e58591b1b1be7714178cCAS | 20007865PubMed |
Csete, M. E., and Doyle, J. C. (2002). Reverse engineering of biological complexity. Science 295, 1664–1669.
| Reverse engineering of biological complexity.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD38Xhsleitbk%3D&md5=fcc99c7baf86ff4137430cd793bdfc7aCAS | 11872830PubMed |
Davidson, E. H. (2006). ‘The Regulatory Genome: Gene Regulatory Networks in Development and Evolution.’ (Academic Press: Oxford.)
Davidson, E. H. (2010). Emerging properties of animal gene regulatory networks. Nature 468, 911–920.
| Emerging properties of animal gene regulatory networks.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXhsFKlsrvM&md5=260bbd8513d99b717cde25f4c28fd5cbCAS | 21164479PubMed |
Davidson, E. H., and Erwin, D. H. (2006). Gene regulatory networks and the evolution of animal body plans. Science 311, 796–800.
| Gene regulatory networks and the evolution of animal body plans.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XhtFyltrc%3D&md5=949c725dc9466f3fd6bf89103830e196CAS | 16469913PubMed |
Erwin, D. H., and Davidson, E. H. (2009). The evolution of hierarchical gene regulatory networks. Nature Reviews. Genetics 10, 141–148.
| The evolution of hierarchical gene regulatory networks.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXlvFChug%3D%3D&md5=aedb3ff00b8fae46412a0371719e68a9CAS | 19139764PubMed |
Erwin, D. H., and Valentine, J. W. (2013). ‘The Cambrian Explosion: The Construction of Animal Biodiversity.’ (Roberts and Company: Greenwood Village, CO.)
Estes, S., and Arnold, S. J. (2007). Resolving the paradox of stasis: models with stabilizing selection explain evolutionary divergence on all timescales. American Naturalist 169, 227–244.
| Resolving the paradox of stasis: models with stabilizing selection explain evolutionary divergence on all timescales.Crossref | GoogleScholarGoogle Scholar | 17211806PubMed |
Gavrilets, S. (2004). ‘Fitness Landscapes and the Origin of Species.’ (Princeton University Press: Princeton.)
Gerhart, J., and Kirschner, M. (1997). ‘Cells, Embryos, and Evolution.’ (Blackwell Science: Oxford.)
Gilbert, S. F., and Epel, D. (2009). ‘Ecological Developmental Biology.’ (Sinauer Associates: Sunderland, MA.)
Gingerich, P. D. (1983). Rates of evolution: effects of time and temporal scaling. Science 222, 159–161.
| Rates of evolution: effects of time and temporal scaling.Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BC3cvitV2isw%3D%3D&md5=9a52dea827b302996421d34ba94fe180CAS | 17741657PubMed |
Gould, S. J. (1980). The promise of paleobiology as a nomothetic, evolutionary discipline. Paleobiology 6, 96–118.
Gould, S. J. (1989). ‘Wonderful Life: The Burgess Shale and the Nature of History.’ (W.W. Norton and Co.: New York.)
Gould, S. J., and Eldredge, N. (1993). Punctuated equilibrium comes of age. Nature 366, 223–227.
| Punctuated equilibrium comes of age.Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DyaK2c%2FltVWktg%3D%3D&md5=bec49647e8697966638380fdd1c82d20CAS | 8232582PubMed |
Green, D. A., and Extavour, C. G. (2012). Convergent evolution of a reproductive trait through distinct developmental mechanisms in Drosophila. Developmental Biology 372, 120–130.
| Convergent evolution of a reproductive trait through distinct developmental mechanisms in Drosophila.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC38XhsVyhtLzM&md5=9728de98c9c05128dd6716e6dd32bea5CAS | 23022298PubMed |
Harper, M. (2009). The replicator equation as an inference dynamic. arXiv:0911.1763v3 [math.DS].
Hendry, P. H., Millien, V., Gonzalez, A., and Larsson, C. E. (2012). How humans influence evolution on adaptive lansdscapes. In ‘The Adaptive Landscape in Evolutionary Biology’. (Eds E. I. Svensson and R. Calsbeek.) pp. 180–202. (Oxford University Press: Oxford.)
Hertel, F. (1994). Diversity in body size and feeding morphology within past and present vulture assemblages. Ecology 75, 1074–1084.
| Diversity in body size and feeding morphology within past and present vulture assemblages.Crossref | GoogleScholarGoogle Scholar |
Hua, H., Pratt, B. R., and Zhang, L. (2003). Borings in Cloudina shells: complex predator–prey dynamics in the terminal Neoproterozoic. Palaios 18, 454–459.
| Borings in Cloudina shells: complex predator–prey dynamics in the terminal Neoproterozoic.Crossref | GoogleScholarGoogle Scholar |
Hunt, G. (2007). The relative importance of directional change, random walks, and stasis in the evolution of fossil lineages. Proceedings of the National Academy of Sciences of the United States of America 104, 18404–18408.
| The relative importance of directional change, random walks, and stasis in the evolution of fossil lineages.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXhtl2ku73E&md5=fc61627e8aeacc3e8b7de6eaabe44b17CAS | 18003931PubMed |
Hunt, G., Bell, M. A., and Travis, M. P. (2008). Evolution towards a new adaptive optimum: phenotypic evolution in a fossil stickleback lineage. Evolution 62, 700–710.
| Evolution towards a new adaptive optimum: phenotypic evolution in a fossil stickleback lineage.Crossref | GoogleScholarGoogle Scholar | 18081713PubMed |
Jones, F. C., Grabherr, M. G., Chan, Y. F., Russell, P., Mauceli, E., Johnson, J., Swofford, R., Pirun, M, Zody, M. C., White, S, Birney, E, Searle, S, Schmutz, J, Grimwood, J, Dickson, M. C., Myers, R. M., Miller, C. T., Summers, B. R., Knecht, A. K., Brady, S. D., Zhang, H, Pollen, A. A., Howes, T, Amemiya, C, Broad Institute Genome Sequencing Platform & Whole Genome Assembly Team Lander, E. S., Di Palma, F, Lindblad-Toh, K, and Kingsley, D. M. (2012). The genomic basis of adaptive evolution in threespine sticklebacks. Nature 484, 55–61.
| The genomic basis of adaptive evolution in threespine sticklebacks.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC38XmtVCis7o%3D&md5=5821fd9d0ae3ab2a26912710996ebb9cCAS | 22481358PubMed |
Kauffman, S. A. (1993). ‘Origins of Order: Self-organization and Selection in Evolution.’ (Oxford University Press: Oxford.)
Lande, R. (1976). Natural selection and random genetic drift in phenotypic evolution. Evolution 30, 314–334.
| Natural selection and random genetic drift in phenotypic evolution.Crossref | GoogleScholarGoogle Scholar |
Lande, R. (1979). Quantitative genetic analysis of multivariate evolution, applied to brain : body size allometry. Evolution 33, 402–416.
| Quantitative genetic analysis of multivariate evolution, applied to brain : body size allometry.Crossref | GoogleScholarGoogle Scholar |
Lewontin, R. C. (1974). ‘The Genetic Basis of Evolutionary Change.’ (Columbia University Press: New York.)
Litt, A., and Kramer, E. M. (2010). The ABC model and the diversification of floral organ identity. Seminars in Cell & Developmental Biology 21, 129–137.
| The ABC model and the diversification of floral organ identity.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXhs1Knu7w%3D&md5=29e8e063975d160b5db29c2144c6d59dCAS |
Lynch, M., and Force, A. (2000). The probability of gene preservation by subfunctionalization. Genetics 154, 459–473.
| 1:CAS:528:DC%2BD3cXms1KhsA%3D%3D&md5=a3e0bd25b5c9c2bc3da153522a75f397CAS | 10629003PubMed |
Marshall, C. R. (1995). Darwinism in an Age of Molecular Revolution. In ‘Evolution and the Molecular Revolution’. (Eds C. R. Marshall and J. W. Schopf.) pp. 1–30. (Jones and Bartlett: Sudbury, MA.)
Marshall, C. R. (2003). Nomothetism and understanding the Cambrian “explosion”. Palaios 18, 195–196.
| Nomothetism and understanding the Cambrian “explosion”.Crossref | GoogleScholarGoogle Scholar |
Marshall, C. R. (2006). Explaining the Cambrian “explosion” of animals. Annual Review of Earth and Planetary Sciences 34, 355–384.
| Explaining the Cambrian “explosion” of animals.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD28XlvFCnurw%3D&md5=d9dd04e776b46a637de7472a77ef6a3dCAS |
Marshall, C. R. (2010). The next 150 years: towards a richer theoretical biology. In ‘Evolution Since Darwin: The First 150 Years’. (Eds M. A. Bell, D. J. Futuyma, W. F Eanes, and J. S. Levinton.) pp. 657–661. (Sinauer Associates: Sunderland, MA.)
Marshall, C. R., and Valentine, J. W. (2010). The importance of preadapted genomes in the origin of the animal bodyplans and the Cambrian explosion. Evolution 64, 1189–1201.
| 19930449PubMed |
McCune, A. R. (1990). Evolutionary novelty and atavism in the Semionotus complex: relaxed selection during colonization of an expanding lake. Evolution 44, 71–85.
| Evolutionary novelty and atavism in the Semionotus complex: relaxed selection during colonization of an expanding lake.Crossref | GoogleScholarGoogle Scholar |
McGhee, G. R. (1999). ‘Theoretical Morphology: the Concept and its Application.’ (Columbia University Press: New York.)
McGhee, G. R. (2007). ‘The Geometry of Evolution. Adaptive Landscapes and Theoretical Morphospaces.’ (Cambridge University Press: Cambridge.)
McKinnon, J. S., and Rundle, H. D. (2002). Speciation in nature: the threespine stickleback model systems. Trends in Ecology & Evolution 17, 480–488.
| Speciation in nature: the threespine stickleback model systems.Crossref | GoogleScholarGoogle Scholar |
McMenamin, M. A. S. (2000). ‘The Garden of Ediacara.’ (Columbia University Press: New York.)
Niklas, K. J. (1994). Morphological evolution through complex domains of fitness. Proceedings of the National Academy of Sciences of the United States of America 91, 6772–6779.
| Morphological evolution through complex domains of fitness.Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DyaK2czhs1GrsA%3D%3D&md5=6c468878de2a0e3df9d41bc636f8d720CAS | 8041696PubMed |
Niklas, K. J. (1997). Effects of hypothetical developmental barriers and abrupt environmental changes on adaptive walks in a computer generated domain for early vascular land plants. Paleobiology 23, 63–76.
Niklas, K. J. (2004). Computer models of early land plant evolution. Annual Review of Earth and Planetary Sciences 32, 47–66.
| Computer models of early land plant evolution.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2cXkvVyju7g%3D&md5=00b42c31d9f8ab47d773d6d0e56ca682CAS |
Pigliucci, M. (2012). Landscapes, surfaces, and morphospaces: what are they good for? (Eds E. I. Svenesson and R. Calsbeek.) pp. 26–38. (Oxford University Press: Oxford.)
Raup, D. M. (1966). Geometric analysis of shell coiling: general problems. Journal of Paleontology 40, 1178–1190.
Rice, S. H. (2004). ‘Evolutionary Theory: Mathematical and Conceptual Foundations.’ (Sinauer Associates: Sunderland, MA.)
Ronquist, F., and Huelsenbeck, J. P. (2003). MrBayes 3: Bayesian phylogenetic inference under mixed models. Bioinformatics 19, 1572–1574.
| MrBayes 3: Bayesian phylogenetic inference under mixed models.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXntlKms7k%3D&md5=544b296d48ad75d42c45092f433e09b6CAS | 12912839PubMed |
Ronquist, F., Teslenko, M., Van der Mark, P., Ayres, D. L., Darling, A., Höhna, S., Larget, B., Liu, L, Suchard, M. A., and Huelsenbeck, J. P. (2012). MrBayes 3.2: efficient Bayesian phylogenetic inference and model choice across a large model space. Systematic Biology 61, 539–542.
| MrBayes 3.2: efficient Bayesian phylogenetic inference and model choice across a large model space.Crossref | GoogleScholarGoogle Scholar | 22357727PubMed |
Salazar-Ciudad, I., and Jernvall, J. (2010). A computational model of teeth and the developmental origins of morphological variation. Nature 464, 583–586.
| A computational model of teeth and the developmental origins of morphological variation.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXivFKntbg%3D&md5=ce452c3391a10f1e978872f6645be9f9CAS | 20220757PubMed |
Schneider, I., and Shubin, N. H. (2013). The origin of the tetrapod limb: from expeditions to enhancers. Trends in Genetics 29, 419–426.
| The origin of the tetrapod limb: from expeditions to enhancers.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3sXivFyks74%3D&md5=0bc96a19af97c3fe8081d5296e3a556eCAS | 23434323PubMed |
Simpson, G. G. (1944). ‘Tempo and Mode in Evolution.’ (Columbia University Press: New York.)
Simpson, G. G. (1953). ‘The Major Features of Evolution.’ (Columbia University Press: New York.)
Slater, G. J., Dumont, E. R., and Van Valkenburgh, B. (2009). Implications of predatory specialization for cranial form and function in canids. Journal of Zoology 278, 181–188.
| Implications of predatory specialization for cranial form and function in canids.Crossref | GoogleScholarGoogle Scholar |
Thompson, J. N. (2005). ‘The Geographic Mosaic of Coevolution.’ (University of Chicago Press: Chicago.)
Tseng, Z. J. (2013). Testing adaptive hypotheses of convergence with functional landscapes: a case study of bone-cracking hypercarnivores. PLoS ONE 8, e65305.
| Testing adaptive hypotheses of convergence with functional landscapes: a case study of bone-cracking hypercarnivores.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3sXpsFemsLk%3D&md5=84832a59c963463d200d0acb1099e9b7CAS | 23734244PubMed |
Van Valen, L. (1973). Festschrift. Science 180, 488.
Van Valen, L. (1974). A natural model for the origin of some higher taxa. Journal of Herpetology 8, 109–121.
| A natural model for the origin of some higher taxa.Crossref | GoogleScholarGoogle Scholar |
Van Valkenburgh, B. (1995). Tracking ecology over geological time: evolution within guilds of vertebrates. Trends in Ecology & Evolution 10, 71–76.
| Tracking ecology over geological time: evolution within guilds of vertebrates.Crossref | GoogleScholarGoogle Scholar |
Vermeij, G. J. (1987). ‘Evolution and Escalation.’ (Princeton University Press: Princeton.)
Wade, M. J. (2012). Wright’s adaptive landscape: testing the predictions of his shifting balance theory. In ‘The Adaptive Landscape in Evolutionary Biology’. (Eds E. I. Svensson and R. Calsbeek.) pp. 58–73. (Oxford University Press: Oxford.)
Wagner, P. J. (2000). Exhaustion of morphological character states among fossil taxa. Evolution 54, 365–386.
| 1:STN:280:DC%2BD3cvgtlKksg%3D%3D&md5=fe76ca868de92b7b0de6e745d4b95ec5CAS | 10937214PubMed |
Wagner, A. (2011). ‘The Origins of Evolutionary Innovations: A Theory of Transformative Change in Living Systems.’ (Oxford University Press: Oxford.)
Wagner, P. J. (2012). Modelling rate distributions using character compatibility: implications for morphological evolution among fossil invertebrates. Biology Letters 8, 143–146.
| Modelling rate distributions using character compatibility: implications for morphological evolution among fossil invertebrates.Crossref | GoogleScholarGoogle Scholar | 21795266PubMed |
Wagner, P. J., and Erwin, D. H. (2006). Patterns of convergence in general shell form among Paleozoic gastropods. Paleobiology 32, 316–337.
| Patterns of convergence in general shell form among Paleozoic gastropods.Crossref | GoogleScholarGoogle Scholar |
Wagner, P. J., Ruta, M., and Coates, M. I. (2006). Evolutionary patterns in early tetrapods. II: Differing constraints on available character space among clades. Proceedings of the Royal Society of London. Series B, Biological Sciences 273, 2113–2118.
| Evolutionary patterns in early tetrapods. II: Differing constraints on available character space among clades.Crossref | GoogleScholarGoogle Scholar |
West, K., and Cohen, A. (1996). Shell microstructure of gastropods from Lake Tanganyika, Africa: adaptation, convergent evolution, and escalation. Evolution 50, 672–681.
| Shell microstructure of gastropods from Lake Tanganyika, Africa: adaptation, convergent evolution, and escalation.Crossref | GoogleScholarGoogle Scholar |
West, K., Cohen, A., and Baron, M. (1991). Morphology and behavior of crabs and gastropods from Lake Tanganyika, Africa: implications for lacustrine predator–prey coevolution. Evolution 45, 589–607.
| Morphology and behavior of crabs and gastropods from Lake Tanganyika, Africa: implications for lacustrine predator–prey coevolution.Crossref | GoogleScholarGoogle Scholar |
Wolfram, S. (2002). ‘A New Kind of Science.’ (Wolfram Media: Champaign, IL.)
Wright, S. (1931). Evolution in Mendelian populations. Genetics 16, 97–159.
| 1:STN:280:DC%2BD2s%2FmsVGqsw%3D%3D&md5=5d7231f9c3a04535156bc1dcb9f0883cCAS | 17246615PubMed |
Wright, S. (1932). The roles of mutation, inbreeding, crossbreeding and selection in evolution. In ‘Proceedings of the Sixth International Congress on Genetics. Volume 1’. (Ed. D. F. Jones.) pp. 356–366. (Austin, TX.)