N-body Simulations with Live Stellar Evolution
Ross P. Church A B D , Christopher A. Tout B and Jarrod R. Hurley A CA Centre for Stellar and Planetary Astrophysics, School of Mathematical Sciences, Monash University, Vic 3800, Australia
B Institute of Astronomy, The Observatories, Madingley Road, Cambridge CB3 0HA, UK
C Centre for Astrophysics and Supercomputing, Swinburne University of Technology, Hawthorn, Vic 3122, Australia
D Corresponding author. Email: ross.church@sci.monash.edu.au
Publications of the Astronomical Society of Australia 26(1) 92-102 https://doi.org/10.1071/AS08062
Submitted: 8 December 2008 Accepted: 2 February 2009 Published: 2 April 2009
Abstract
An N-body code containing live stellar evolution through combination of the software packages nbody6 and stars is presented. Operational details of the two codes are outlined and the changes that have been made to combine them discussed. We have computed the evolution of clusters of 104 stars using the combined code and we compare the results with those obtained using nbody6 and the synthetic stellar evolution code sse. We find that, providing the physics package within stars is set up correctly to match the parameters of the models used to construct sse, the results are very similar. This provides a good indication that the new code is working well. We also demonstrate how this physics can be changed simply in the new code with convective overshooting as an example. Similar changes in sse would require considerable reworking of the model fits. We conclude by outlining proposed future development of the code to include more complete models of single stars and binary star systems.
Keywords: stars: evolution — stars: mass-loss — methods: N-body simulations — methods: numerical — open clusters and associations: general
1 Introduction
The gravitational N-body problem — the motion of a set of massive bodies under mutual self-gravity — is one of the oldest in computational astronomy. The first simulations were carried out by Holmberg (1941) who used special-purpose hardware. As computing power has increased, particularly with the introduction of the GRAPE hardware (Makino & Taiji 1998) and computational algorithms have improved it has become possible to include greater numbers of particles and more sophisticated physics in order to make more accurate models of star clusters, galaxies and the Universe itself. To study the evolution of galactic and globular open clusters we must integrate the motion of each particle separately, considering the force contribution from each of the other particles. Because of the high densities in the cores of stellar clusters particles can approach very close to one another and we must include special procedures to prevent such encounters introducing unacceptable errors.
To make physically realistic models of stellar clusters we cannot avoid considering the evolution of the stars themselves. Mass loss from stars changes the cluster’s potential and hence affects the motion of its stars. Furthermore the finite radius of a star means that if it approaches close to another they may interact. Tidal dissipation may cause a bound binary system to form, within which matter can be transferred from one star to another, and stars that come sufficiently close may merge. To predict the evolution of the mass and radius of a star with time it is necessary to use a stellar evolution code. Stellar evolution is another area of computational astronomy with a considerable heritage. A procedure for evaluating numerical models of stars by use of an electronic computer was outlined by Haselgrove & Hoyle (1956). Over the years such simulations have grown in detail and accuracy as more physics has been added and more powerful computers have become available for the integration of the equations. In the past however the computational cost of these calculations has prohibited including them in cluster simulations.
The most popular approach to date for including stellar evolution in cluster models has been the use of synthetic stellar evolution codes. This involves analytic fits made to the results of a full code evaluated to simulate the evolution of a star. A prime example is the sse code of Hurley, Pols & Tout (2002) which was derived from the detailed models of Pols et al. (1998). The combination of synthetic stellar evolution and N-body dynamics has been used to good effect to model the interplay between stellar and dynamical evolution in star clusters (Portegies et al. 2001; Baumgardt et al. 2003; Hurley et al. 2005). However, a major drawback is that the fitting process is laborious and the result inflexible, in that it relies on choices made in generating the underlying set of detailed models. If the input physics used for the detailed models becomes out of date in any way then so does the synthetic package and it is non-trivial to generate a new set of analytic fits. It is also ill-equipped to deal with non-equilibrium cases arising from binary mass-transfer and stellar collisions. The pioneers of the synthetic stellar evolution approach were Eggleton, Fitchett & Tout (1989) who preferred this to the main alternative at the time which was interpolation within a database of detailed models. It was decided that such a database would be cumbersome — especially if a large grid of models of various mass and metallicity were required — and create problems for data storage. Fortunately this is not a major issue anymore and the interpolation approach does have its merits. The ideal is to perform live stellar evolution in combination with N-body dynamics and to also include a module for dealing with any stellar collisions that arise, for example the smooth particle hydrodynamics of Sills et al. (2003).
Computing power has increased in recent times to the point where it is possible to combine a full stellar evolution code with a N-body code. We present here such a code and compare the results to those obtained with synthetic stellar evolution. Section 2 contains details of the two codes that we used and the models that we compare are described in Section 3. The results are presented in Section 4 and discussed in Section 5.
2 Description of the Code
We give a brief description of some of the relevant features of the two codes, stars and nbody6, along with the modifications that have been necessary to combine them.
2.1 stars
stars, the Cambridge Stellar Evolution code, was originally written by Eggleton (1971) and has been extensively modified since (see Pols et al. 1995 and references therein for a complete description). stars utilises the method of Henyey, Forbes & Gould (1964). The equations of stellar structure are written as implicit finite difference equations on a mesh and solved by numerical inversion of the resulting matrix. The mesh has a fixed number of meshpoints that can move in both mass and radius, and hence is neither Eulerian nor Lagrangian. The model is written in terms of the quantities log f (a measure of electron degeneracy as described by Eggleton, Faulkner & Flannery 1973), temperature, mass, radius, luminosity, the mass fractions of hydrogen, helium-4, carbon-12, oxygen-16 and neon-20 and a quantity Q which determines the position of the mesh. In a converged model the gradient of Q is equal at all points on the mesh. It has an ad-hoc functional form that causes more points to be placed where the temperature, mass, pressure and radius are varying most quickly. These are the regions, such as burning shells and ionisation zones in the atmosphere, that need to be well resolved. The system of equations is then solved by a relaxation method. The timestep in stars is controlled by the user-supplied parameter Δ. After a model has converged the next timestep is calculated as
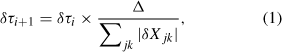
where δXjk is the change in variable j at meshpoint k. The sum is evaluated over all the variables except the luminosity. A larger value of Δ allows the variables to change more in a single timestep and hence larger timesteps are taken. Convective overshooting can be included by means of a modified Schwarzschild criterion controlled by a single parameter δov; details of the implementation are described in Schröder, Pols & Eggleton (1997).
2.1.1 Zero-Age Models
The models described in this paper were all calculated at solar composition, X = 0.7, Y = 0.28 and Z = 0.02. A library of zero-age main-sequence models of masses between 0.1 M⊙ and 100 M⊙ has been produced by a multi-stage process. We took a stellar model of uniform solar composition and inserted an artificial energy source to inflate it into a cold, low-density cloud until the core temperature was below 106 K, below which no nuclear reactions are modelled by the code. We then added and removed mass to produce a pre-main sequence of models of low density and temperature. We removed the artificial energy source and followed the contraction down to the point of minimum radius to produce a set of models with self-consistent central compositions and temperatures. By adding a small amount of mass to the envelope of one of these models we can construct models of zero-age main-sequence stars with any mass.
2.1.2 The Helium Flash
We have developed a routine to pseudo-evolve through the helium flash in low-mass stars. In stars less massive than about 2.3 M⊙ the core is degenerate at the time of helium ignition so that the increased temperature owing to helium burning does not cause expansion and thermal runaway occurs (Schwarzschild & Härm 1962). To evolve through the helium flash with stars requires very small timesteps, which lead to numerical instability in calculation of the luminosity. To circumvent these problems we construct approximate post-flash models with stable core helium burning. A star of mass M ≃ 3 M⊙ that has evolved successfully through non-degenerate core helium ignition is taken and matter removed from the envelope until the desired mass is reached. The hydrogen burning shell is then allowed to burn outwards with helium consumption disabled in order to obtain the correct core mass and the envelope compositions reset to their pre-flash values. Normal evolution is then resumed. Whilst not physically rigorous this process provides models that can be used to simulate subsequent evolution.
2.1.3 Mass Loss
We have written a simple procedure to determine the type of a star (main sequence, red giant, etc.) from the central abundances and hydrogen, helium and carbon burning luminosities of the star. Then we automatically choose an appropriate mass-loss law for the star according to:
-
Main sequence, no mass loss;
-
Red giant branch (RGB), Reimers mass loss (Kudritzki & Reimers 1978)
-
with η = 0.4;
-
Core helium burning, Reimers mass loss with η = 1.0;
-
Asymptotic giant branch (AGB), Vassiliadis & Wood (1993) mass loss
-
-
White dwarf (WD), no mass loss.
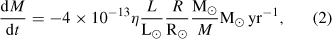
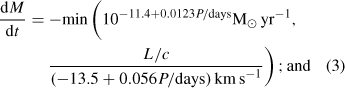
2.1.4 Timestep and Mesh Size
To reduce model runtime and memory requirements we use a relatively low resolution (199 meshpoints per model). Runtime is further decreased by choosing a comparatively large value of the timestep parameter, Δ = 5, which ensures rapid progress throughout the star’s life. These two choices have the added advantage of suppressing thermal pulses on the AGB, which are too computationally demanding and numerically difficult to be included in these models (Stancliffe, Tout & Pols 2004).
2.1.5 The Post-AGB
Some extra procedures are necessary to complete the evolution of the stars from the late AGB to the white dwarf cooling track. This phase of evolution, known as the post-AGB, is even more numerically demanding than the AGB phase that proceeds it. To prevent numerical convergence issues arising from very high luminosities, once the stars have entered the superwind phase the rates of the triple-alpha and CNO reactions are capped at 10–12 and 10–11 reactions per baryon per second. Unmodified, stars experiences a cyclical phase of evolution where fierce burning in the shell causes the very light envelope to be blown off. The shell extinguishes and then reignites as the envelope contracts back on to the star. This is both slow to converge, as many hundreds of cycles can occur even in the presence of strong mass loss and frequently causes code non-convergence. This behaviour is thought to be a numerical artefact of the stars code though its cause is unclear (Stancliffe 2005). In order to surpress these cycles, once the hydrogen-burning shell reaches 0.02 M⊙ from the surface of the star the rate of energy generation from nuclear burning is further reduced such that
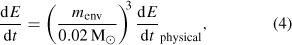
where m env is the envelope mass (mass between the shell and surface of the star). The rate of consumption of material remains at the physical value, however, so the overall effect is to make the remaining nuclear burning produce less energy.
As these procedures are both implemented only after the superwind phase of mass loss has begun, which truncates the AGB, they have very little effect on the observable evolution. The most apparent consequence is that the luminosity on the post-AGB is reduced by about 0.5 dex; however, this phase is very short-lived and hence unlikely to be observed: no post-AGB stars appear in the HR diagrams plotted in Figures 1 to 3. The principal effect of these two additional procedures is to render the predicted surface compositions of white dwarfs unreliable. These compositions are not trustworthy anyway because we do not model thermal pulses, which radically alter the compositions of AGB stars. We have found this procedure sufficient to evolve stars of initial masses up to 4 M⊙ for a few Gyr, the typical lifetime of the clusters under consideration.
2.1.6 Binaries
The only element of binary stellar evolution implemented at present is the collision of stars. This is handled in a very simple manner. A zero-age star of the same mass as the combined mass of the two colliding stars is generated. Other interactions within binaries that form dynamically are ignored.
2.2 nbody6
nbody6 is a general-purpose full force summation N-body dynamics code. A general description of the development of nbody6 and its sister codes is reviewed in Aarseth (1999) and an exhaustive description of its algorithmic basis, construction and operation is given in a recent book (Aarseth 2003). It uses the Ahmad & Cohen (1973) neighbour scheme to reduce the cost of computation for large models, where the forces from particles lying within some local neighbour radius are updated more frequently than those from particles lying further away. An Hermite integrator is used with individual hierarchical timesteps. To remove the accuracy and performance problems associated with integrating perturbed binaries around many orbits Kustaanheimo & Stiefel (1965) regularisation is used. This involves a change of variables in four dimensions, with one fictitious dimension added to make the transformation possible, as well as a time scaling. For perturbed hierarchical configurations (triples, quadruples, etc.) chain regularisation (Mikkola & Aarseth 1990) is used. By default nbody6 uses the synthetic stellar evolution code sse (Hurley, Pols & Tout 2000).
To integrate stars with nbody6 the procedures that involve calls to sse have been re-written and a set of subroutines added to provide an interface between the two codes. To interrogate the state of star N at time t a routine has been written that extracts the required quantities from the live stellar evolution models at the time t (the evolution and N-body codes have independent time steps). As a star evolves a model may occasionally fail to converge; in that case stars restarts from the previous time with a reduced timestep. Hence it is possible for values at the current timestep to change, because the restarted model may have different evolution. To avoid information provided to the N-body code being subsequently revised we ensure that the time for which the data are requested is between the previous and anteprevious timestep, i.e. that
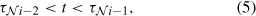
where τ Ni is the latest stellar evolution time for star N. If this is not the case then the model for star N is loaded into memory and evolved for the necessary number of timesteps. Once this has been done the radius, mass and luminosity at time t are calculated by linear interpolation between adjacent stellar models and returned. A time for the next interrogation of the stellar model is also provided to nbody6. It is calculated as the maximum time in which the radius should not change by more than 2% or the mass by more than 1%. An arbitrary limit of ten stars timesteps is also imposed, preventing nbody6 advancing past any interesting phases of evolution that start suddenly.
3 Model Setup
To investigate the differences between models with synthetic and full stellar evolution five cluster models, each containing 104 stars, were evolved with our combined code. For the purposes of comparison we also evolved two clusters with the same initial conditions but with synthetic stellar evolution. Subsequent analysis of the models produced caused us to run another model with full stellar evolution and convective overshooting, with the parameter δov = 0.12 as in the construction of the sse models. All stellar models started from the zero-age main sequence and had metallicity Z = 0.02.
The stars are all taken to be single; there are no primordial binaries. The masses of the stars are distributed at random from a Kroupa, Tout & Gilmore (1993) initial mass function (IMF), obtained from the generating function
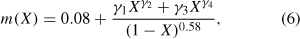
where X is a number randomly chosen from the uniform distribution in the range [0,1], γ1 = 0.19, γ2 = 1.55, γ3 = 0.05 and γ4 = 0.6. The initial positions of the particles are distributed according to the Plummer distribution,
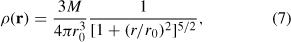
where M is the total cluster mass and r 0 is a scaling factor related through integration to the half-mass radius rh by rh ≃ 1.3 r 0. Following the standard approach for N-body units and initial conditions we set M = 1 and r 0 = 1. The distance scaling of the simulation is then determined by specifying the physical extent of the N-body length unit. We choose this to be 2 pc for all these simulations which, along with the IMF and imposition of initial virial equilibrium, defines the scaling. More details can be found in Aarseth (2003). A standard tidal field based on Oort’s constants (Oort 1927) is applied which places the cluster at Sun’s position in the Galaxy. We take Oort’s constants to be A = 14.4 km s–1 kpc–1 and B = –12.0 km s–1 kpc–1. The initial conditions for the five models were identical except for the random number generator seed which was changed to give a different set of masses, positions and velocities for the stars. Hence the models can be considered to be a small, representative sample of possible 104 star clusters with that set of initial conditions.
4 Results and Comparison
We extracted various different properties from the data output by the code, chosen to measure different aspects of the stellar evolution and dynamics of the clusters in an attempt to determine how much the simulations differ. We have considered the quantities as a function of the fraction of stars remaining instead of time because this is more characteristic of the dynamical state of evolution of the cluster and hence there is less scatter between the lines. In the case of the graph of the time against fraction of stars remaining this is counterintuitive but aids comparison with the other graphs in the paper. For most of the quantities we have also plotted the standard deviation of the values from the five standard models (full stellar evolution without convective overshooting). The points when the models have a certain fraction of stars remaining are not exactly coincident. Consequently we have interpolated the quantities to a standard set of points. This is a reasonable approach to take for quantities that are varying slowly, i.e. on a timescale longer than the interval between the snapshots of the cluster that the code produces. This standard deviation provides a measure of the spread of values owing to the variation within the population of clusters of the type that we are considering. Furthermore we have calculated the mean of the five standard models at each of these points and subtracted it from the models using sse and stars with convective overshooting to get a set of residuals. By comparing these residuals with the standard deviations we measure whether the different stellar evolution prescriptions significantly change the models.
4.1 HR Diagrams
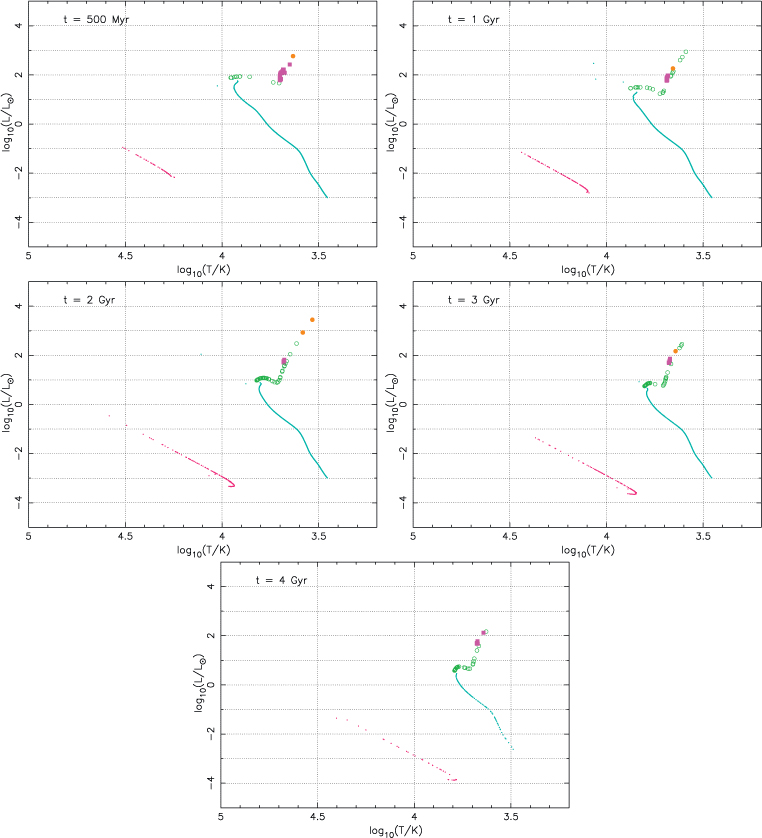
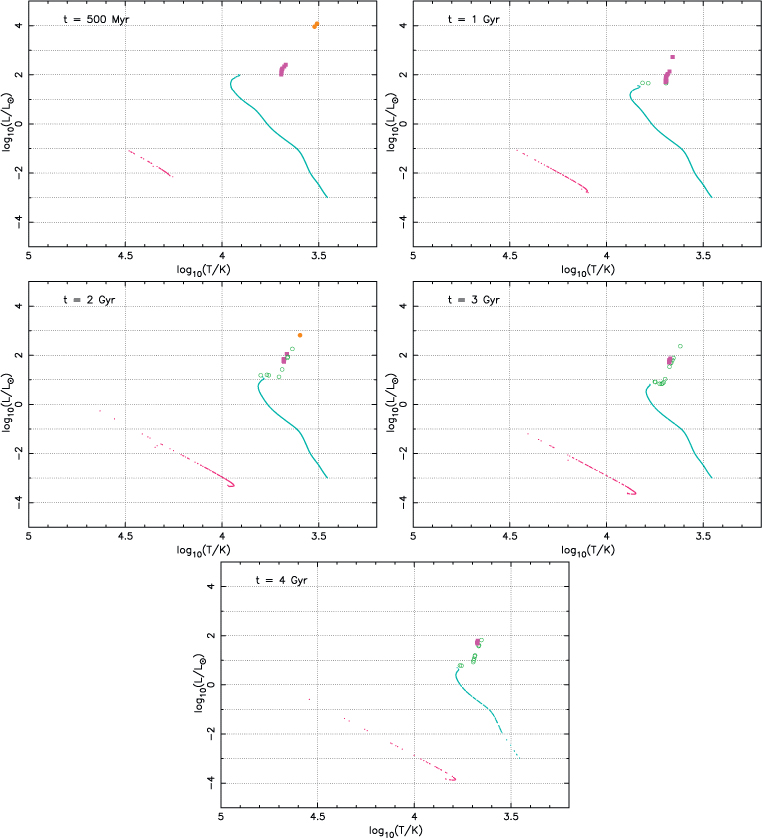
The HR diagram of an actual cluster is relatively easily observed; only photometry and the distance to the cluster are required for absolute magnitudes. Similarly the theoretical version, the luminosity–temperature diagram, is easily generated as the temperature and luminosity are always calculated by a stellar evolution code. Comparison of the two requires bolometric correction via fits to detailed models of stellar atmospheres. However, even given the uncertainties in this process, such diagrams provide a powerful and widely-used tool for comparing models and observations of clusters. Hence producing an accurate HR diagram is an important function of the stellar evolution section of a hybrid code. Figure 1 contains HR diagrams for snapshots from one of the stars models without convective overshooting, Figure 2 HR diagrams for one of the sse models and Figure 3 diagrams for the stars model computed with convective overshooting.
4.2 Stellar Type Fractions and Mass
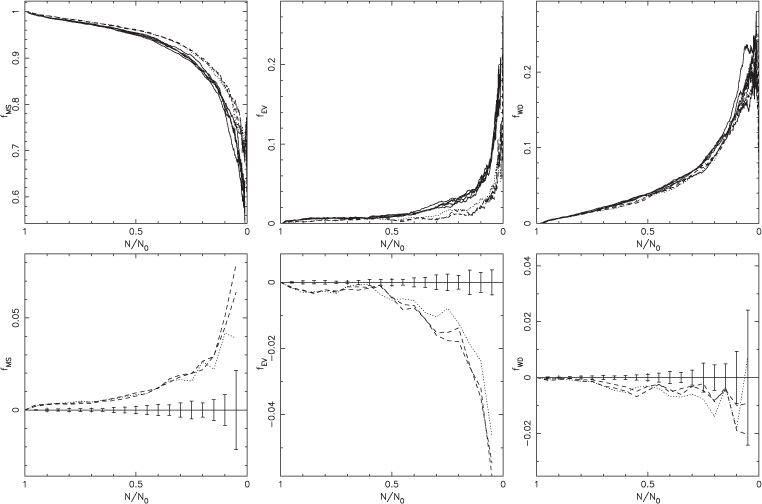
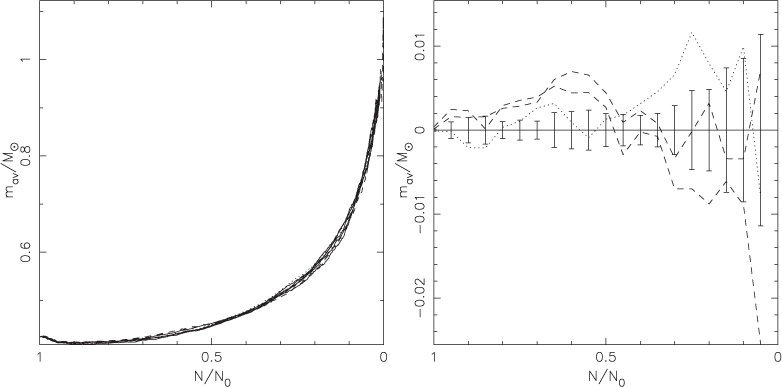
At the beginning of a model cluster’s life its constituent stars are all on the zero-age main sequence. As time passes stars both evolve and are lost from the cluster. Both these processes affect the fraction of stars that are of a given type and hence these properties depend on both dynamics and stellar evolution. Figure 4 contains diagrams showing the evolution of the various stellar type fractions. The same processes also affect the average stellar mass, the evolution of which is shown in Figure 5. The conversion of the fraction of stars remaining to time can be found from Figure 6.
|
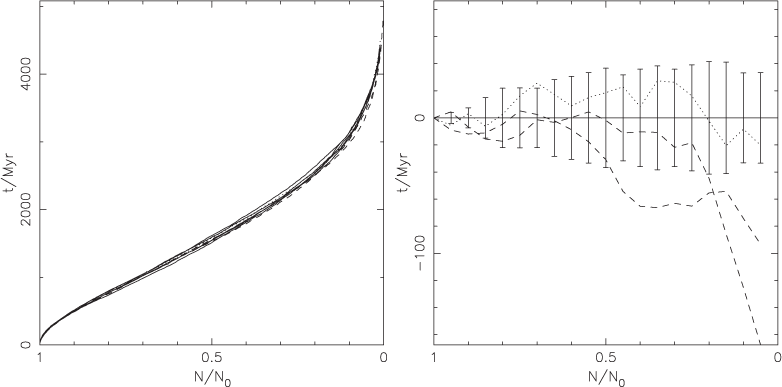
4.3 Time Against Number of Stars
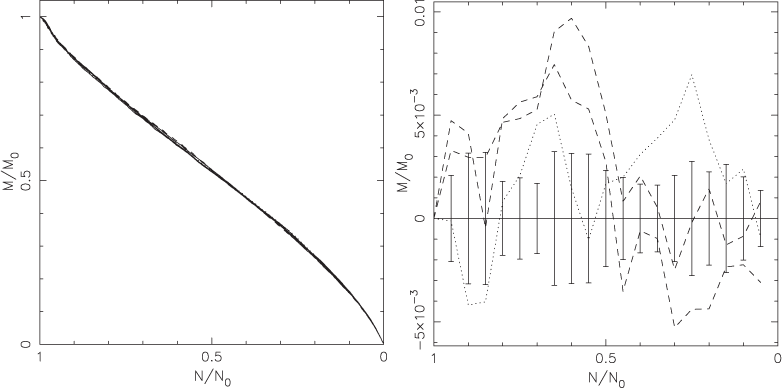
Stars escape from a cluster by evaporation. Few-body interactions exchange energy between stars and an energy-gaining star can become unbound and escape from the cluster. This process is accelerated by the presence of the Galactic tidal field. Simultaneously the cluster loses mass because of evaporation, stellar winds and supernovae. This reduces the strength of the cluster potential and hence increases the evaporation rate. Thus the cluster mass and the number of stars remaining are tracers of dynamical processes happening on a smaller scale. A plot of the time taken for the fraction of stars remaining to fall to a given level is shown in Figure 6 and a plot of the fraction of the initial mass remaining in Figure 7.
|
4.4 Core and Half-Mass Radii
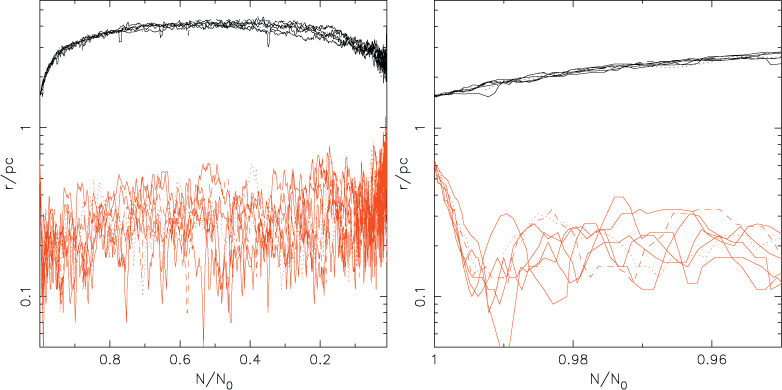
The core is the most important part of a stellar cluster. In the core densities are highest, so the closest encounters between stars take place. The crossing time of the core is smaller than that of the whole cluster, so catastrophic collapse owing to the gravothermal instability takes place there first. The core radius is the standard indicator of how large and how dense the core is, whilst the half-mass radius allows us to measure the behaviour of the outer parts of the cluster. A plot of the evolution of the core and half-mass radii with time is presented in Figure 8.
5 Comparison and Discussion
The results show that the behaviour of the different codes is very similar, with some small differences which we discuss individually.
5.1 Stellar Measures
Comparing Figures 1 and 2 several differences can be seen. The Hertzsprung gap in the stars model is much more populated; this is particularly evident at 2 Gyr. The turnoff mass is lower in the stars models because their main-sequence lifetimes are shorter. Finally the minimum white dwarf temperatures in the stars models are higher suggesting that they are cooling more slowly. This occurs even though the turnoff mass is lower, which implies that the white dwarfs formed earlier.
The first two differences are caused by the presence of convective overshooting in the models from which sse was constructed. Convective overshooting — the mixing of material outside the boundaries of convective regions in stars — is a possible explanation for the extra mixing over and above normal convective mixing that it thought to take place in stars (Shaviv & Salpeter 1973). Amongst the several effects it has on evolution, described in Schröder et al. (1997), it extends the main-sequence lifetime and reduces the time spent crossing the Hertzsprung gap. The set of HR diagrams in Figure 3, for a cluster run using stars with convective overshooting, show that the first two differences largely disappear. Although there are still one or two more stars in the Hertzsprung gap the difference is not substantial. The differences in the white dwarf cooling track are caused by the over-simplified physics included in the version of sse that we were using. This has been remedied in more recent versions.
The overall trend in the evolution of the stellar type distributions, as shown in Figure 4, is that the fraction of main-sequence stars decreases as the cluster evolves whereas the fractions of white dwarfs and evolved stars increase. The decline in main-sequence star numbers is caused by stars evolving off the main sequence and the preferential evaporation of low-mass stars which are predominantly on the main sequence. The number of white dwarfs is larger than the number of evolved stars other than at very early times because the evolved stars subsequently evolve further into white dwarfs. On the other hand as the cluster approaches dissolution the fraction of evolved stars increases much more rapidly, because these are now some of the heaviest stars in the cluster and hence the last to be lost.
Again it can be seen from the plots of residuals that the inclusion of convective overshooting has a significant effect on cluster evolution. The fraction of main-sequence stars in the two models with convective overshooting (the sse models and the stars model with convective overshooting) decline less quickly than in the stars model without convective overshooting, particularly at the expense of evolved stars. For stars of intermediate mass overshooting enlarges the convective core causing more hydrogen to be burnt and hence increasing the main-sequence lifetime. The sse models and the stars model with convective overshooting are seen to agree within the intrinsic variability of the problem given by the error bars.
5.2 Dynamical Properties
Comparing the results for sse and stars in Figure 6 we can see that for most of the models the total number of stars and mass of stars in the cluster are in good agreement between the two codes. The sse models have fewer stars towards the end of the evolutionary sequence (after about half the stars have been lost from the simulations). To explain this difference it is useful to consider first the average stellar mass.
We can see in Figure 5 that the average stellar mass behaves similarly across all the models. Initially it declines slightly owing to mass loss from the most massive stars and then increases following the preferential evaporation of low-mass stars. From the plot of the residuals we see that until about half the stars in the cluster have been lost the sse models have higher average masses. This is because the inclusion of convective overshooting increases the main-sequence lifetimes of intermediate-mass stars. This in turn increases the turnoff mass and hence the mean stellar mass. However as the cluster evolves the stars at the turnoff have smaller and smaller convective cores and so the difference in lifetimes is less pronounced. The residuals of the average mass for the stars model with convective overshooting shows a similar trend but displaced downward slightly, as the mean mass drops more sharply at the beginning of the simulation. This is presumably because there are, by chance, a larger number of the highest mass stars in the simulation. These effects are also clear in the plot of the total mass remaining in the cluster (Figure 7).
The effect of this enhanced number of more massive stars appears to be to increase the rate of ejection of stars from the cluster. This explains the number of stars being lower in the sse models from the point where half the stars have evaporated onwards. However, one should be aware of reading too much into the results; few of the differences are significant beyond two standard deviations.
From the plot of core and half-mass radii (Figure 8) it is hard to glean much interesting information. Looking at the half-mass radius we can see that the cluster expands initially, owing to mass loss from evolving stars, then remains at roughly constant size for most of its lifetime and shrinks towards the end as it dissolves. The core radius declines sharply at the start of the simulation, undergoes core collapse just prior to 200 Myr and behaves erratically thereafter. No significant deviation between the different sets of stellar models can be identified.
6 Conclusions
We would expect, a priori, that the introduction of full stellar evolution would have a limited effect on cluster simulations containing only single stars because the synthetic stellar evolution fits are generally found to be good for single stars. These results show that this is indeed the case. Once convective overshooting has been included in the models they fit the results obtained with sse to within the intrinsic variability of the calculations.
One of the benefits of a live stellar evolution code is the increased flexibility that it brings. In order to change the value of the convective overshoot parameter, the mixing length parameter for convective mixing, the initial elemental abundances, or any other aspect of the physics package, inside stars we merely a change one or two parameters. This contrasts with a synthetic code where a whole new grid of models must be computed and fits made to them. Hence a live code, whilst not offering much improvement in accuracy for single stars, does provide additional flexibility. The new code allows us to produce, for instance, stellar isochrones and luminosity functions that incorporate the effect of dynamics, whilst also allowing us to vary aspects of the stellar physics such as the mixing and initial chemical compositions.
To make full use of detailed stellar evolution models we need to extend the code described here. The problems with numerical non-convergence on the late AGB/post-AGB need to be solved for stars of mass greater than 4 M⊙ so that we can simulate the whole range of masses of single stars. The next step will then be to add the effects of binary interactions. Interactions are very significant for the dynamical evolution of clusters and binaries are responsible for the formation of many different types of stellar exotica, including blue stragglers, X-ray binaries, millisecond pulsars, etc. For a full description of cluster evolution, this important (and often difficult) area of evolution needs to be modelled properly. Such processes as Roche Lobe overflow and common envelope evolution must be included. Work on developing the code further to this end is underway.
Acknowledgments
The authors would like to thank Sverre Aarseth for the use of the nbody6 N-body code and much patient assistance during its adoption and use; without his help this work would have not been possible. R.P.C is grateful to PPARC for a scholarship and to the Australian Research Council Discovery Project for support under grant DP0663447. C.A.T is grateful to Prof. John Lattanzio for funding his sabbatical leave in Australia and to Churchill College Cambridge for a fellowship. J.R.H is grateful to the Australian Research Council for a fellowship.
Aarseth,
S. J. 1999, PASP, 111, 1333
An error has occurred in (ref id="R1").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
241
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:241)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Aarseth,
S. J. 2003, Gravitational N-Body Simulations (Cambridge University Press),
An error has occurred in (ref id="R2").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
243
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:243)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Ahmad,
A., & Cohen,
L. 1973, JCoPh, 12, 389
An error has occurred in (ref id="R3").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
243
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:243)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Baumgardt,
H., Makino,
J., Hut,
P., McMillan,
S., & Portegies Zwart,
S. 2003, ApJ, 589, L25
An error has occurred in (ref id="R4").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
241
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:241)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Eggleton,
P. P. 1971, MNRAS, 151, 351
An error has occurred in (ref id="R5").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
243
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:243)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Eggleton,
P. P., Faulkner,
J., & Flannery,
B. P. 1973, A&A, 23, 325
An error has occurred in (ref id="R6").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
243
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:243)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Eggleton,
P. P., Fitchett,
M. J., & Tout,
C. A. 1989, ApJ, 347, 998
An error has occurred in (ref id="R7").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
241
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:241)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Haselgrove,
C. B., & Hoyle,
F. 1956, MNRAS, 116, 515
An error has occurred in (ref id="R8").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
243
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:243)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Henyey,
L. G., Forbes,
J. E., & Gould,
N. L. 1964, ApJ, 139, 306
An error has occurred in (ref id="R9").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
241
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:241)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Holmberg,
E. 1941, ApJ, 94, 385
An error has occurred in (ref id="R10").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
241
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:241)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Hurley,
J. R., Pols,
O. R., & Tout,
C. A. 2000, MNRAS, 315, 543
An error has occurred in (ref id="R11").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
241
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:241)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Hurley,
J. R., Pols,
O. R., & Tout,
C. A. 2002, MNRAS, 329, 897
An error has occurred in (ref id="R12").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
241
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:241)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Hurley,
J. R., Pols,
O. R., Aarseth,
S. J., & Tout,
C. A. 2005, MNRAS, 363, 293
An error has occurred in (ref id="R13").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
241
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:241)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Kroupa,
P., Tout,
C. A., & Gilmore,
G. 1993, MNRAS, 262, 545
An error has occurred in (ref id="R14").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
243
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:243)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Kudritzki,
R. P., & Reimers,
D. 1978, A&A, 70, 227
An error has occurred in (ref id="R15").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
243
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:243)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Kustaanheimo,
P., & Stiefel,
E. 1965, J. Reine Angew. Math., 218, 204
An error has occurred in (ref id="R16").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
243
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:243)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Makino,
J., & Taiji,
M. 1998, Scientific simulations with special-purpose computers : The GRAPE systems (Chichester; Toronto: John Wiley & Sons),
An error has occurred in (ref id="R17").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
243
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:243)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Mikkola,
S., & Aarseth,
S. J. 1990, CeMDA, 47, 375
An error has occurred in (ref id="R18").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
241
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:241)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Oort,
J. H. 1927, BAN, 3, 275
An error has occurred in (ref id="R19").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
243
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:243)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Pols,
O. R., Tout,
C. A., Eggleton,
P. P., & Han,
Z. 1995, MNRAS, 274, 964
An error has occurred in (ref id="R20").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
243
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:243)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Pols,
O. R., Schroder,
K.-P., Hurley,
J. R., Tout,
C. A., & Eggleton,
P. P. 1998, MNRAS, 298, 525
An error has occurred in (ref id="R21").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
241
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:241)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Portegies Zwart,
S. F., McMillan,
S. L. W., Hut,
P., & Makino,
J. 2001, MNRAS, 321, 199
An error has occurred in (ref id="R22").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
241
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:241)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Schröder,
K.-P., Pols,
O. R., & Eggleton,
P. P. 1997, MNRAS, 285, 696
An error has occurred in (ref id="R23").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
243
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:243)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Sills,
A., et al. 2003, NewA, 8, 605
An error has occurred in (ref id="R24").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
241
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:241)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Schwarzschild,
M., & Härm,
R. 1962, ApJ, 136, 158
An error has occurred in (ref id="R25").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
241
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:241)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Shaviv,
G., & Salpeter,
E. E. 1973, ApJ, 184, 191
An error has occurred in (ref id="R26").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
241
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:241)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Stancliffe,
R. J. 2005, PhD Thesis, University of Cambridge,
An error has occurred in (ref id="R27").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
243
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:243)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Stancliffe,
R. J., Tout,
C. A., & Pols,
O. R. 2004, MNRAS, 352, 984
An error has occurred in (ref id="R28").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
241
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:241)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML
Vassiliadis,
E., & Wood,
P. R. 1993, ApJ, 413, 641
An error has occurred in (ref id="R29").
Variable LPAGE is undefined. [empty string]
array
1
struct
COLUMN
0
ID
??
LINE
241
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:241)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
2
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
180
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
3
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
177
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
4
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
176
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
5
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
170
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
6
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
15
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
7
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
12
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
8
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
11
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
9
struct
COLUMN
0
ID
CF_INCLUDEJOURNALREF_B
LINE
1
RAW_TRACE
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
TYPE
CFML
10
struct
COLUMN
0
ID
CFINCLUDE
LINE
3230
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
11
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3217
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
12
struct
COLUMN
0
ID
CF_ARTICLE
LINE
3216
RAW_TRACE
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
13
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
2938
RAW_TRACE
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
TEMPLATE
G:\www\publishha\app\modules\journal\Article.cfc
TYPE
CFML
14
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
146
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
15
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
16
struct
COLUMN
0
ID
CF_GENARTICLECONTENT
LINE
1
RAW_TRACE
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
TEMPLATE
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
TYPE
CFML
17
struct
COLUMN
0
ID
CFINCLUDE
LINE
10
RAW_TRACE
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
TEMPLATE
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
TYPE
CFML
18
struct
COLUMN
0
ID
CFINCLUDE
LINE
30
RAW_TRACE
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
19
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
241
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
20
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
327
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
21
struct
COLUMN
0
ID
CF_UDFMETHOD
LINE
39
RAW_TRACE
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
TEMPLATE
G:\www\publishha\app\controller\CacheController.cfc
TYPE
CFML
22
struct
COLUMN
0
ID
CF_CFPAGE
LINE
634
RAW_TRACE
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
TEMPLATE
G:\www\publishha\app\PublishingApp.cfc
TYPE
CFML
23
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
16
RAW_TRACE
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
TEMPLATE
G:\www\publishha\app\Bootstrap.cfc
TYPE
CFML
24
struct
COLUMN
0
ID
CF_TEMPLATEPROXY
LINE
18
RAW_TRACE
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
TEMPLATE
G:\www\publishha\webroot\Application.cfc
TYPE
CFML