Gordon Elliott (Tim) Wall, 11 March 1925–13 July 2023
Gustav Lehrer A *
A *
A
Abstract
G. E. (Tim) Wall was one of Australia’s leading algebraists, whose work intersected many of the important algebraic themes of his era (roughly 1960–95). This biographical memoir follows his life from his birth in 1925 in Adelaide, through his professional career, mostly at the University of Sydney, giving some details of his family, personal interactions and research.
Keywords: algebra, group theory, invariants, matrix theory, quadratic forms, Tim Wall.
Early life
Gordon Elliott (universally known as ‘Tim’, for reasons to be explained shortly) Wall was born in Adelaide on 11 March 1925 and passed away in Sydney on 13 July 2023 (Fig. 1). Both his parents were people of some distinction.
His mother, Annie Winifred Wall (née Clark), was one of the two first female graduates in Medicine in South Australia. She was a general practitioner (GP), specialising in anaesthetics, for her working life. Later, she was one of the founders of the Royal ANZ College of Anaesthetists. Tim’s father, Frederic Lawrence Wall (1892–1958) was a surgeon and military hero; in World War 1, he was at Gallipoli and in the Somme, receiving a Military Cross and Croix de Guerre for his exploits. In World War 2, he was still active as an army surgeon, and was deployed to Papua New Guinea. The Wall family had been established in South Australia since the 1850s.
Tim was sent to the premier private college in Adelaide, St Peters School, where he excelled academically and was an enthusiastic, if not particularly gifted, sportsman. He was particularly distinguished in mathematics and Latin. He was a slow left arm spin bowler in the School cricket team, whose coach was a star fast bowler, Thomas Welbourn Wall, who was a teacher at the school, and also an international cricketer of renown, and a teammate of Don Bradman. His nickname was ‘Tim’. It was because of this connection that people replaced the original ‘Elliott’ by which he had been known, by ‘Tim’.
He had three sisters—Margaret, Kathleen and Ellen—but he was the ‘golden boy’ of the family. When he was just fifteen, he took the final public examination, and received a ‘credit in each subject, and was the top student in South Australia overall. However, he was too young to go to university, and so repeated the year at school, obtaining the same result in the final exam.
University and marriage
In 1941 Tim enrolled in first year Medicine at the University of Adelaide. He was under some pressure from his parents, particularly his father, to follow in their medical footsteps. He had little inclination to study medicine, however, and in particular he found anatomy a subject that repelled him, to the extent that he ceased attending the lectures. It was a family legend that he was once found during an anatomy lecture, in his room smoking, and listening to classical music.
He soon switched to his real vocation, mathematics, and thrived thereafter, notwithstanding his father’s concern about how a mathematician could ever earn a living.
At university, Tim always said that he was enormously influenced by Professor Hans Schwerdtfeger, a German refugee from the Nazis, who had been born in Göttingen and studied at university there. At the time, Göttingen was probably the leading pure mathematical centre in the world, and Schwerdtfeger attended lectures by such household (mathematical) names as David Hilbert, Gustav Herglotz, Richard Courant, James Franck, Max Born and Bartel van der Waerden. Schwerdtfeger had left Germany in 1936, and after an eventful journey, took a Lectureship at Adelaide in 1940. Tim therefore serendipidously had an excellent grounding in the subjects which Schwerdtfeger taught him: Galois theory, matrix theory, theory of groups and their geometries and complex analysis. I myself learned linear algebra from a course given by Tim at the University of Sydney in the 1960s. It was a masterpiece of precision and economy.
In 1948 Tim married Jean Ann Hamilton (1924–2015) who had trained as a scientist, and later worked at Fisher Library. They met at the University of Adelaide where she was also an undergraduate. They had four children: Geoffrey, Pip, Jo and Michael.
Postgraduate life
After completing his Honours degree at the University of Adelaide, Tim went to Cambridge, where he wrote a PhD thesis in 1951, entitled ‘The Galois Theory of Binomial Equations’, under the supervision of J. W. S. Cassels. He wrote a joint paper with Cassels on the normal basis theorem (a Galois-theoretic theme) in 1950,1 and a longer paper on the Galois group of a binomial polynomial,2 which was the topic of his thesis. It is interesting that Tim acknowledges Walter Ledermann and Hans Schwerdtfeger for ‘valuable advice’, and states that the problems was suggested to him by Professor Schwerdtfeger. One might speculate that J. W. S. Cassels was Tim’s ‘supervisor’ only in a formal sense, and that his thesis was written independently.
At the time of his departure in 1948, he and Jean were engaged, but Jean had taken a position as a researcher at the Walter and Eliza Hall Institute in Melbourne (where Sir Frank Macfarlane Burnett was the Director), so she travelled separately to England, where she and Tim were married (Fig. 2).
Career
In 1952 Tim went to the University of Manchester as a Lecturer. There he met many distinguished mathematicians, such as Max Newman, Berhard Neumann, Alan Turing, James Lighthill, Kurt Mahler, J. A. Green and others. From Manchester, he moved on to the University of Newcastle-upon-Tyne and in 1956 departed for the University of Sydney, where he stayed, first as senior lecturer, then reader, and from 1965, professor. He became Emeritus Professor in 1990 at the age of 65.
In the meanwhile, he had been elected a Fellow of the Australian Academy of Science in 1971, and served as President of the Australian Mathematical Society from 1970 to 1972.
Mathematical research
Classification of the conjugacy classes in the unitary, symplectic and orthogonal groups
Tim’s most famous work is undoubtedly a paper published in 1963 that was reviewed effusively by Jean Dieudonné,3 one of the world’s top mathematicians of the day. Dieudonné was a ‘Bourbakist’, a group of mainly (but not only) French mathematicians who were undertaking the project of writing all mathematics in a systematic way. Their numerous books were published under the pseudonym Nicolas Bourbaki (Fig. 3).
Dieudonné writes in his review of Wall’s paper that the work is ‘without a doubt definitive, written in the most general context, and resolves two problems of which innumerable special cases have been addressed over the last century, by a no less innumerable set of authors, who often worked in ignorance of previously established results’.4
The two problems are as follows. Given a group G and an element g ∈ G, a conjugate of g is any element of G of the form xgx−1 (for some x ∈ G). The set of all elements conjugate to g is known as its conjugacy class; the group G is the disjoint union of its conjugacy classes.
Describe the set of conjugacy classes of the group of isometries (length preserving transformations) of a space over a skew field K. (These are known as the ‘classical groups’).
A ‘sesquilinear form’ on the K-space V is a ‘length function’ f: V × V → K, which is sesquilinear and non-degenerate (not necessarily symmetric, skew, …). Problem: classify all such forms.
Problem A could be interpreted as: assign an (algebraic) invariant to each class of G, so that all possible invariants exhaust the classes, and they are all distinct. Tim showed first that the two problems are equivalent, and then proceeded to give definitive solutions to each. It is worth noting that these are not mathematical bywaters. They are central to many mathematical themes to this day. In fact there are now more modern treatments of Problem A, based on algebraic geometric methods (that is, far more sophisticated), but significantly, the most detailed and far reaching results remain in Tim’s treatment.
This classical work of Tim’s has had something of a renewal recently, because of the upsurge in interest in computational and probabilistic group theory.
Wall’s conjecture on the number of maximal subgroups of a finite group
In his 1961 paper,5 Tim analyses in detail several aspects of the structure and classification of p-groups. These are notoriously known as ‘wild’ problems, but undaunted, Tim proved several very significant results. He was able to leverage these into the following statement.
For any finite group G, let max(G) denote the number of maximal subgroups of G. Then for any soluble group G, we have max(G) ≤ |G|.
Wall’s conjecture: the above inequality holds for any finite group G.
To the best of my knowledge, this remains unresolved to this day. It has been generalised to infinite dimensional C*-algebras, and there is an enormous literature, proving variants of this statement in special cases, but none as clean as the original.
Brauer–Suzuki–Wall
In his 1963 paper,6 Tim gives an abstract characterisation of the simple groups PSL2(q), where q ≥ 4 is a prime-power, with two of the leading group theorists of the 20th century: Richard Brauer and Michio Suzuki. Specifically, it is shown that if an abstract group G satisfies the following three conditions, then G is one of the groups PSL2(q). The conditions are: (i) |G| is even; (ii) If G has two cyclic groups C1, C2 such that C1 ∩ C2 ≠ 1, then G has a cyclic group C such that C ⊇ C1 and C ⊇ C2; (iii) G is equal to its derived group, i.e. is generated by its elements of the form xyx−1y−1.
The significance of this result is that it is one of the very early ‘characterisation’ results; it was an important step in the classification of all final simple groups. It should be mentioned that the paper’s origins were not as a joint project. Tim proved the result independently, and they decided to combine forces later. Ronald Solomon, in his History of the Classification of Finite Simple Groups, writes: ‘By 1954, Wall, Brauer and Suzuki had their own version of a characterisation of PSL2(q)’. Their work was combined and published some years later as.7
This work is among the few that are described in detail in Gorenstein’s classic book on Finite Groups,8 whose purpose was to set an agenda for the classification of all finite simple groups, which was achieved some years later.
Clifford collineation groups and Weil representations
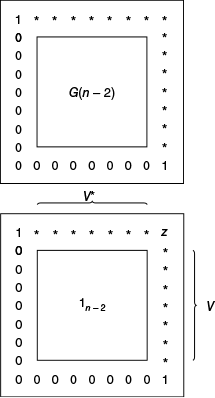
In 1961–2, Tim wrote a series of four papers,9 some with co-authors Beverley Bolt and T. G. Room, on what is effectively a connection between the theory of multilinear forms, sometimes integral, and group representations. In his case, the relevant representations were of matrix groups over a finite field. In 1964, André Weil, possibly the most influential mathematician of the twentieth century, wrote his celebrated work Sur certaines groupes d’opérateurs unitaires,10 Weil’s most cited work. Weil’s work was a ‘continuous version’ of the Wall–Bolt–Room work, but the crux was to show that certain representations, which were a priori projective, are actual representations. I will illustrate this with a picture. Suppose we have a sequence of groups G(n), such that G(n) is a group of n × n matrices, and G(n − 2) may be realised inside G(n) as shown in Fig. 4.
It is evident that the group G(n − 2), as depicted in the top diagram, acts on V ⊕ V*, where V = Kn−2, K being the ground field with a possible twist. The ‘V’ here can be identified with the last column of the bottom matrix, with the top element removed while V* is the top row. The top right element encodes the cocycle z. Both Weil and Bolt–Room–Wall show that this cocycle is trivial. This example is intended to show that Tim was involved in many of the major mathematical themes of the day, in this case, the theory of ‘Weil representations’.
This subject now has an enormous literature, and is often referred to as the theory of ‘metaplectic representations’.
This work, together with the related theme of automorphism groups of lattices,11 has now acquired extra significance through the works of Nebe–Rains–Sloane, in that it is now known to relate cryptography to classical invariant theory.
Summary
These four examples suffice to show that Tim was deeply involved in several of the major mathematical themes of his day, themes which have persisted for the almost seventy years since he did this work. Although he was not outstandingly productive, there is a simplicity and elegance about his work, which has at times enabled him to see further than others.
References
Barnes, E. S., and Wall, G. E. (1959) Some extreme forms defined in terms of abelian groups, Journal of the Australian Mathematical Society, 1(1), 47-63.
| Crossref | Google Scholar |
Bolt, B., Room, T. G., and Wall, G. E. (1961a) On the Clifford collineation transform and similarity groups. II, Journal of the Australian Mathematical Society, 2(1), 80-96.
| Crossref | Google Scholar |
Bolt, B., Room, T. G., and Wall, G. E. (1961b) On the Clifford collineation transform and similarity groups. I, Journal of the Australian Mathematical Society, 2(1), 60-79.
| Crossref | Google Scholar |
Brauer, R., Suzuki, M., and Wall, G. E. (1958) A characterization of the one-dimensional unimodular projective groups over finite fields, Illinois Journal of Mathematics, 2, 718-745.
| Crossref | Google Scholar |
Cassels, J. W. S., and Wall, G. E. (1950) The normal basis theorem, Journal of the London Mathematical Society, 25, 259-264.
| Crossref | Google Scholar |
Wall, G. E. (1953) The Galois group of a binomial polynomial, Proceedings of the London Mathematical Society, s3-3, 195-210.
| Crossref | Google Scholar |
Wall, G. E. (1961) Some applications of the Eulerian functions of a finite group, Journal of the Australian Mathematical Society, 2, 35-59.
| Crossref | Google Scholar |
Wall, G. E. (1962) On the Clifford collineation, transform and similarity groups (IV): an application to quadratic forms, Nagoya Mathematical Journal, 21, 199-222.
| Crossref | Google Scholar |
Wall, G. E. (1963) On the conjugacy classes in the unitary, symplectic and orthogonal groups, Journal of the Australian Mathematical Society, 3, 1-62.
| Crossref | Google Scholar |
Wall, G. E. (2001) Multiplicity-free quotient tensor algebras, Journal of the Australian Mathematical Society, 71, 279-297.
| Google Scholar |
Weil, A. (1964) Sur Certaines groupes d'op‚rateurs unitaires, Acta Mathematica, 111(0), 143-211.
| Crossref | Google Scholar |