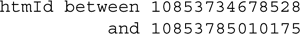An astronomy catalogue lists a collection of objects and their features, for example location, magnitude and colour. All sky catalogues have been constructed from systematic surveys of the night sky where one or more telescopes are dedicated to perform repeated observations. During this process, the same patch of sky will be observed multiple times and a catalogue constructed by merging data.
This paper reports an investigation comparing the performance of two popular database systems, mysql and oracle, using sql queries on catalogues consisting of approximately a billion objects. This is the size expected of the catalogue generated from the Stromlo Southern Sky Survey (S4) using the SkyMapper telescope currently under construction1. Catalogues of this size currently exist and benchmarking tests have been carried out on a selection of these as well.
The investigation shows that large catalogues can be handled effectively with a modest computing environment. It is advisable, however, to be aware of specific deployment and implementation options available with each of the database systems adopted.
The paper starts with a review of related work before describing the computing environment and catalogues used. The first tests are a selection of typical queries expected by the astronomy community. This is followed by cone search queries, which highlight the need for a spatial index to improve query performance. The task of finding neighbours within a catalogue is then detailed along with the related operation of catalogue cross matching. A summary and discussion of the results concludes the paper.
An extended version of this investigation is available as a CSIRO ICT Centre Technical Report (Power 2006).
The performance of general catalogue queries is covered in Gray et al. (2002) where they detail the implementation of twenty queries for the Sloan Digital Sky Survey (SDSS) (Szalay et al. 2000) using the Microsoft sql sever database. These tests were however conducted on a dataset much smaller, 14 million rows. Their results cannot be directly compared with those reported here since every aspect is different: hardware, software and data.
The Hierarchical Triangular Mesh (HTM) spatial index (Kunszt et al. 2000) can be used to efficiently perform cone search and other location based queries. While there are other spatial indexing schemes for astronomy datasets,2 detailed performance comparisons have not been reported.
Modern database systems provide support for data types other than numbers and strings. The type system of a database may be extensible allowing new user defined types and operations to be introduced. All the major database vendors support spatial data types in some form or other with standardisation efforts evolving3. The user base for these activities is from the Geographical Information Systems community which uses Earth based datasets. The coordinate systems are spheroidal rather than spherical, making it inefficient to measure distances when the data points use a spherical polar coordinate system. There are no known attempts to utilise these capabilities with astronomy datasets.
Neighbour finding is addressed in the field of computational geometry where optimal solutions use techniques that assume a complex data structure, for example the Voronoi tessellation or the Delaunay triangulation (Preparata 1985). These structures are computationally expensive to establish and the algorithms would need to be modified to work in a spherical polar coordinate system. The adaptation of these algorithms and structures for use in the astronomy domain remains untested.
The work of Gray et al. (2004) describes an approach to finding neighbours in sql that uses declination partitions termed zones. Each object is uniquely associated with a zone: neighbours are first determined within a zone and, only when necessary, neighbours between zones evaluated. This approach reduces the search space for an individual object to a more manageable size, but within zones it uses a nested loop approach where each object is compared with all others to find neighbours.
openskyquery4 allows astronomy catalogues to be cross matched. For example, a personal catalogue of objects can be used for cross matching against a selected database. The algorithm used is the foundation for a distributed query engine allowing catalogues at different locations to be merged using a likelihood analysis to determine if objects match or not. Cross matching performance using openskyquery for large catalogues is not documented.
A brief description of the computing environment and the catalogues used is presented below.
Computing
The machine used for benchmarking was a Dell Power Edge 2650 server with dual Pentium Xeon 2 GHz CPUs, 2 GB main memory and 6 TB disk. The maximum transfer rate between the disk and the server is 160 Mbytes/sec. The operating system is Debian Linux 2.6.8.
The database systems used are mysql 5.0 Community Edition, Generally Available (GA) Release5 and oracle 10.2.06. The databases were installed ‘out of the box’. The table and column names were kept identical so the same sql query syntax could be used interchangeably for each database. All tests are measured in terms of elapsed time, the total time taken to complete the test as reported by the computer's internal clock.
The benchmarking tests were performed using the same Java application for both databases. All tests are performed on a ‘cold’ database, one that has just been shut down and restarted and the operating system's disk cache flushed. The neighbour finding and cross matching code is implemented in c++.
Catalogues
The original purpose of benchmarking was to profile the expected database performance using a large synthetic catalogue constructed to simulate the characteristics expected from SkyMapper. Code to generate a realistic stellar S4 dataset was provided (P. Francis 2004, private communication) for this purpose. Large non-synthetic astronomy catalogues are also available
and a small selection were also tested. These extra datasets provide a comparison of the synthetic dataset with realistic ones. They also allow the catalogue cross matching operation to be investigated.
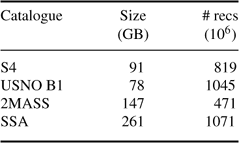
A brief description of each catalogue follows with a summary in Table 1.
Table 1: Catalogue Summary
|
The synthetic S4 dataset simulates a stellar population that is realistic in its magnitude and sky distribution for the southern hemisphere. The randomly generated magnitudes adopt an extension of the UGRIZ system used in the SDSS and is described at the SkyMapper homepage1.
The US Naval Observatory (USNO) has published a series of catalogues all based on digitising photographic plates. The B1.0 (Monet et al. 2003) is the latest, referred to as USNO B1 in this paper, and contains over one billion objects compiled from 7435 Schmidt plates, describing their position, proper motion and magnitudes in various optical passbands.
Each record in the catalogue is derived from up to five surveys and each survey includes a star/galaxy estimator flag. The original focus of this report was to investigate stellar datasets, so it was considered to extract the stellar records. Using the star/galaxy estimator, if only one flag is set to indicate the record is a star, then there are around 615 million stars, approximately 60% of the dataset. If all flags are required to agree that a record is stellar, then roughly 21 million (2%) are found.
The benchmarking reported here concerns database performance, not science astronomy results, and so the whole dataset was loaded and issues of identifying stellar records not considered further.
The Two Micron All Sky Survey (2MASS) (Skrutskie et al. 2006) contains point and extended source catalogues of the near infra-red sky. The point source catalogue contains positions and uniformly calibrated photometry of nearly 500 million point sources while the extended source catalogue consists of over 1.5 million spatially extended sources, mainly galaxies.
Only the point source catalogue has been investigated here.
The SuperCOSMOS Science Archive (SSA) (Hambly et al 2001) comprises data extracted from scans of photographic Schmidt survey plates, similar to the USNO catalogues. The resulting object detections form a catalogue of over one billion records covering the southern celestial hemisphere.
A copy of the SSA Source Table consisting of stellar and galaxy data was obtained from the Royal Observatory of Edinburgh. As mentioned for USNO B1, the entire dataset was loaded and issues of identifying stellar objects ignored.
Database performance was initially assessed using examples motivated from the SDSS and SSA. Only the S4 was tested since this corresponds to the size and content of a catalogue expected from SkyMapper, the focus of this investigation. Appendix A contains a brief description of the queries with a complete listing available in Power (2006).
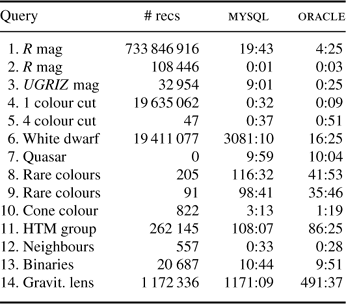
The query performance is shown in Table 2. Note that database indexes have been created on the appropriate table columns to ensure efficient query processing.
Table 2. Query Performance (mm:ss)
|
The first two queries are the same except for the tested R magnitude value, resulting in more records found which significantly increases its elapsed time. The third query includes extra magnitude conditions to check, reducing the number of records found, but requires more work by the database.
Queries 4 and 5 use magnitude differences, a ‘colour cut’, and are efficiently performed by each database.
The performance of the search for white dwarf stars was a surprise. It is a simple variation from the previous query, but was the worst for mysql and one of the slowest for oracle.
The quasar query involves a complicated stellar model and contains the most complicated sql where clause tested.
The next four queries, 8–11, test aggregation using the sql group by clause. These are slow queries but when a cone search region is included (Query 10) the spatial index makes the query faster.
The last three queries are examples of self-joins to find neighbours. Queries 12 and 13 target close objects by testing a small angular separation and are able to find a result within an acceptable time. The same can not be said for Query 14 where it takes over eight hours to complete for oracle and nearly 20 hours for mysql.
In summary, oracle is significantly faster (by a factor of 3) than mysql for half the queries, and about the same for the remainder. All the queries were performed adequately by each database, other than the last (a time-consuming join operation) and Query 6 for mysql.
The next set of tests were cone searches, a location query defined as: find all the objects within a certain radius of a given location on the celestial sphere.
Cone Search
A cone search query is performed by calculating the great circle distance from the cone centre to each target object and testing if this distance is within the required radius. An example sql query that uses the spherical law of cosines to find the records within a 0.25-degree radius of the location 134.154, –15.137 in degrees is shown in Figure 1.
Figure 1 Cone search sql.

|
This query uses the s4_sub table, an S4 subset of approximately 74 million records used to check the queries before running them on the full S4 table. In all 9309 matching records are found and it takes just under three minutes for mysql and nine and a half hours with oracle. This large disparity in elapsed time is due to oracle being very slow when using trigonometric functions and the use of a user defined radians function, a provided function in mysql, but not oracle.
An efficient cone search requires indexing.
Spatial Indexing
There are numerous indexing schemes to support spatial data, see Gaede & Gunther (1998) for a survey. The Hierarchical Triangular Mesh (HTM) spatial index (Kunszt et al. 2000) uses area decomposition. The celestial sphere is initially divided into eight spherical triangles: four for the north and four south. Each triangle is then divided into four and the process repeated recursively to a predetermined depth. The triangles are numbered with the aim of preserving spatial proximity: areas close spatially are labeled with numbers that are also numerically close. The labels are mapped to a base-10 integer value termed the ‘HTM id’.
The HTM source distribution includes sql server specific functions as stored procedures (non standard sql extensions) to efficiently use the HTM spatial index. For example, the fGetNearbyObjEq function implements cone search.
In order to use the HTM spatial index, one solution would be to port the stored procedure code to each database system. This was not pursued because, apart from not wanting to port the code twice, the version of mysql originally used in this investigation did not support stored procedures. While the current version of mysql does, the decision had been taken early on that HTM support could be manifested externally to the database system by modifying the sql queries as explained below. This has the advantage that databases which don't support stored procedures can be included in the assessment.
The functionality of the HTM spatial index can be used without stored procedures. Using the same cone search example from Figure 1, a 0.25 degree radius around the location 134.154, –15.137, an area on the celestial sphere encompassing the cone region is specified in terms of HTM id's by the condition:
This query fragment is evaluated by the function fGetNearbyObjEq. By modifying a user query to include the above where clause fragment, the benefit of the HTM spatial index can be utilised without requiring extensions to standard sql.
In summary, a cone search query can be efficiently implemented in a database by generating a single HTM id for each point object location, creating an index on the HTM id column and generating queries that use HTM ranges in the sql where clause.
Performance
Power (2006) reports twelve sql query versions that perform a cone search using HTM id's in conjunction with various cone search expressions. For example using a haversine (Sinnott 1984), normalised Cartesian coordinates or the expression used in Figure 1. For each sql query version, 500 random RA and Dec locations are generated and eight different cone search radii are used: 5, 15, 30 and 60 arcsec; then 5, 15, 30 and 60 arcmin. In all, over 40 000 queries are tested for each database.
Since the queries are placed randomly over the southern hemisphere, differing numbers of records are found, but the same cone search should find the same records regardless of which of the twelve query versions is used. This was true for oracle, but not always for mysql. This is believed to be due to issues of precision in floating point arithmetic or the implementation of trigonometric functions.
The consistently best performing query version was to use normalised Cartesian coordinates and include the cone's Minimum Bounding Rectangle (MBR) as well as the HTM id's. This is necessary in oracle in order to achieve acceptable query response times (avoiding trigonometric functions) and is advisable in mysql since it produces consistent results.
An example of such a query is shown in Figure 2, the same cone search as Figure 1, but expressed differently in sql. Note the successive refinement in the query. The HTM id's are used as a coarse filter, then the MBR of the cone used as a further refinement before using the dot product between the two normalised Cartesian coordinates to test against the cosine of the cone search radius. There are no trigometric or radian functions used in the sql, all expressions are pre-computed when generating the query.
Figure 2 Fastest-cone search.

|
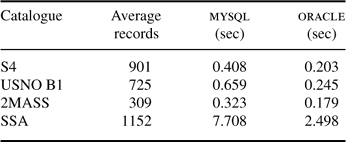
Table 3 reports the average elapsed times for each catalogue using a search radius of 5 arcmin. oracle consistently performs two to three times faster than mysql.
Table 3. Cone search, radius 5 arcmin
|
Sorting
Database query performance can be improved by sequencing the table data in the same order as the index. This allows the table data to be accessed sequentially, improving disk I/O. When the index is on the htmId column then this also groups spatially close objects nearby on disk. For example, given a sql query with the following where clause:
The index on the htmId column is used to find the disk references for the corresponding table data. If the table and index records are stored in ascending order of HTM id, then the table data will be read from disk sequentially, making better use of disk reads.
The effect of re-sequencing the data was tested by sorting each dataset by the htmId values before loading into the database and repeating the cone search queries. The results for each catalogue when using a cone search radius of 5 arcmin is shown in Table 4, the same tests as reported earlier in Table 3.
Table 4. HTM sorted data radius 5 arcmin (sec)
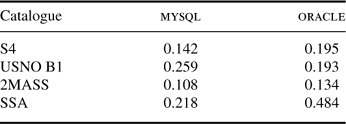
|
The improvement is dramatic for mysql, around three times faster than the original queries. There is only a small speedup for oracle, apart from the SSA result, and now both systems have similar performance.
The next problem tested was neighbour finding: for each object in the catalogue, find the neighbours within a specified angular distance occurring in the same catalogue.
Various approaches to identifying neighbours were performed on a subset of the synthetic dataset. These variations are explained below. The best approach of those tested is to use software to generate a list of neighbours, recording for each pair their record ids and angular separation, then loading the result into the database. This is the approach used in the SuperCOSMOS and SDSS archives.
SQL
Finding the nearest neighbours for all objects within a catalogue can be achieved using standard sql. The query in Figure 3 finds all pairs of records in S4 within 15 arcsec of each other using an expression involving normalised Cartesian coordinates to determine the angular separation between points. Note the record ids are tested (!=) to ensure the same record is not matched with itself.
Figure 3 sql neighbour finding.

|
Six sql variations of this neighbour finding query were tested in both databases on an S4 data subset with less than 100 000 records. The fastest query took an hour to complete and the slowest more than four.
Plane Sweep
A plane sweep solution was implemented next. This is an algorithmic technique used extensively in computational geometry to solve problems in two dimensional datasets. The data is first sorted in one dimension then an imaginary line is ‘swept’ along the sorted dimension and points processed as they are encountered.
The standard algorithm has been adapted for astronomy catalogues by accommodating the spherical geometry as described in Devereux et al. (2005). Notably:
-
care must be taken at the poles;
-
the sweep line distance requires cos(Dec) corrections;
-
RA wrap around must be considered.
The implementation in a database can not be performed using standard sql: procedural language extensions are required. This was only done for oracle, with a full description provided in Power (2006).
This solution improves performance from over an hour using the standard sql solution, above, to 6.5 min but is still much slower, by orders of magnitude, when compared to a c++ implementation that generates the same results in less than 10 sec.
This code has been adopted by the Royal Observatory Edinburgh where they use it to generate lists of neighbours. Their previous implementation took 48 hours to process a billion rows of data whereas now it takes five hours (R. Collins 2005, private communication).
Performance
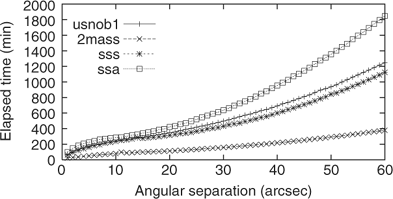
Figures 4 and 5 show the performance of the c++ implementation (Devereux et al. 2005) of the plane sweep neighbour finding algorithm for each catalogue using angular separations ranging from 1 to 60 arcsec. The results of Figure 4 do not include the time to write the result to disk: the tests simply count the number of matching records.
Figure 4 Neighbour-finding times.
|
Figure 5 Neighbour-finding records.
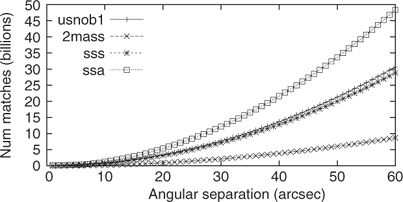
|
Note that the USNO B1 and SSA tables both have around one billion objects, but SSA takes longer to process. This is because the SSA data is spatially denser than the USNO B1: the SSA table only covers the southern hemisphere whereas the USNO B1 covers the entire celestial sphere. The impact is that more neighbours will be found for SSA which requires more data processing as the sweep line encounters points in the sorted dataset.
The plane sweep algorithm to find neighbours requires the catalogue to be sorted in ascending sequence of Dec. Only the object location (RA and Dec) and unique identifier are required. The location is needed since it is used to determine proximity to other objects, while the id is used to record the result.
The results reported in Figure 4 do not include the time to sort the data by Dec. This pre-processing is accomplished by extracting the requisite information then sorting using specifically written software and takes between 1:30–2:15 hours to complete for each of the four catalogues tested.
Cross matching is similar to finding neighbours, except now there are two datasets. The task is: given two catalogues, for each object in one, find the objects in the other that are within a specified angular separation.
The algorithm reported in Devereux et al. (2005) requires location error information to establish a statistical measure of the likelihood that two objects match. The matching reported here used the same software, modified to test a fixed radius, reporting all objects within the circle that match from the other catalogue.
Performance
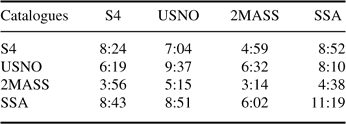
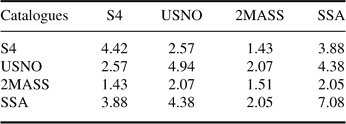
The cross matching tests are performed as a pair wise comparison of the four test catalogues, each prepared by extracting the spatial description along with their unique identifier and sorted as done for neighbour finding (the same input files used for neighbour finding are used for cross matching). Table 5 summaries the elapsed time in hours for cross matching the various catalogues while Table 6 shows the number of records found, in billions. These tests include the time taken to write the results to disk.
Table 5: Cross-matching times (hh:mm)
|
Table 6: Cross-matching records (109)
|
sql solutions were not attempted given the previous poor performance for neighbour finding and the similarity in algorithm.
These results show that the cross matching algorithm is more efficient when the smaller catalogue is used against a larger one. For example, it takes 4:38 to match 2MASS against SSA and 6:02 to match SSA against 2MASS. This is due to the processing performed when the sweep line encounters a point and relates to the density of the catalogue in the dimension in which the dataset is processed.
When catalogues of similar size are cross matched using the Devereux et al. (2005) algorithm the dataset with lower spatial density should be used ‘first’. For example, matching USNO B1 against the SSA takes 8 hours 10 minutes whereas doing it in reverse takes 8 hours 51 minutes.
One of the underlying assumptions not addressed here is that a database is the right environment for publishing a large catalogue such as the S4. The justification extends beyond astronomy specific issues and relates to the ease of data access available through the sql query language. An alternative would be to develop software in c or fortran to process the data with the aid of libraries for efficiently accessing astronomy datasets, such as wcstools7. However, the expressive power and simplicity of sql can not be equalled in such a design.
A relational database provides a simple means of accessing astronomy catalogues. Important operations allowing data selection are feasible, making thorough exploration of the data to be achieved.
This report profiles queries for large catalogues residing in the mysql and oracle database systems. The tests were a selection of typical queries expected by users from the astronomy community, cone search, neighbour finding and cross matching. Most queries, other than neighbour finding and cross matching, were handled adequately by each database system.
oracle was consistently faster than, or the same as, mysql for the general queries tested on the S4 table. Cone search is well supported using the HTM as a spatial index in conjunction with an MBR constraint. oracle was originally between 2–3 times faster than mysql for cone search queries. However, sorting the catalogues as a pre-processing step before database loading improves query response times for cone search, dramatically for mysql, such that the databases now report similar query response times as each other.
Neighbour finding for a catalogue of a billion objects can be achieved in around 6.5 hours: 2 hours preparation (extract location and record id, then sort by Dec) and around 4.5 hours to find the neighbours, depending on the target angular separation required. Similarly, cross matching two catalogues consisting of a billion objects can be achieved in around 12 hours: under 4 hours to prepare the two catalogues and just over 8 hours to do the matching itself. These two operations are not well supported for large catalogues in a database environment when only using sql.
There are further avenues that could be explored. Parallelism of neighbour finding and cross matching using the zone approach from Gray et al. (2004) could yield improvements to the plane sweep algorithm. oracle supports parallelism using partitioning, where a single table is distributed across file systems in a way understood by the query optimiser. Query execution can then be distributed across file systems utilising multi-processor machines, as it is completely transparent from the user perspective. mysql can be installed on a loosely coupled computing cluster as a means of managing scalability.
The tests reported here define a baseline performance; there could be optimisations available that would improve response times. Databases are complex systems and optimal performance is often only achieved after careful tuning of the disk used, operating system configuration, database specific parameters and sometimes the sql queries themselves. The results presented here have been achieved with minimal attention to these aspects.
Appendix: S4 Catalogue Queries
The 14 queries tested in Catalogue Queries are briefly described below with the sql commands for a few presented.
The first two queries examine the impact of a query that counts fewer/more rows in the database by adjusting the rmag threshold. Query 1 tests for rmag values less than 21.75 while Query 2 tests for values less than 12.6.
Query 3, shown below, tests all ugriz magnitudes for values less than 12.6.
Query 3: ugriz magnitude query
Queries 4–6 use magnitude differences to express colour constraints. The colour cut used in Query 6 below is from Gray et al. (2002) where it is described as a search for white dwarf stars.
Query 6: A search for white dwarf stars
Query 7 is also from Gray et al. (2002) and aims to find stars that match a quasar at redshift between 5.5 and 6.5. The query constraint is representative of a user query corresponding to a non-trivial stellar model and is the most complicated selection query tested.
Query 7: User-defined stellar model to find quasars
Query 8 is adapted from Gray et al. (2002) where binning the magnitude differences using the group by clause to convert them to integers is discussed. The resulting data is sorted using the order by clause and the output column names have been relabelled.
Query 9 is the same as Query 8 except that it includes the clause: having count (*) <500 to restrict the number of results found per group.
Query 10 uses the HTM index to query a large region of the sky in conjunction with a simple colour cut. Query 11 is similar except that a different colour cut is defined and there is no cone search restriction.
Query 8: Find objects rare in colour space
The remaining three queries, 12–14, are examples of a self-join. The neighbour table (s4_nn) records pairs of close stars by listing the records id's and angular separation in arc seconds up to a threshold of 10 arcsec. The neighbours are calculated as described in Finding Neighbours and the result loaded into the databases.
Query 12 finds stars very close together, within 0.0083 arcsec, with one of the UGRIZ magnitudes having a variation greater than 0.1. Query 13 finds binary stars where one of the stars has the colour of a white dwarf using the same colour selection as Query 6.
Query 14: Gravitational-lens query
The last query finds objects that are close to each other and have similar colours, which could be used to identify gravitational lens events. Whereas the previous two queries use small angular separations to find objects very close together, this time a large portion of the neighbour's table will be selected since one-quarter of the records are within 5 arcsec.
This work would not have been possible without access to large astronomy catalogues. Thanks go to David Monet and his colleagues at the USNO for providing a copy of the USNO B1 catalogue; Nigel Hambly and Bob Mann for access to the SuperCOSMOS data; Paul Francis for the script to generate a realistic S4 synthetic catalogue; and to the 2MASS team for responding to an email with a set of five double-sided DVDs.
Thanks also to CSIRO staff Dave Abel, Drew Devereux and Peter Lamb for the original work on neighbour finding and cross matching.
This investigation was undertaken as partial fulfillment of the requirements for the Graduate Diploma in Science at the Australian National University supervised by Dr. Paul Francis.
References
Devereux, D., Abel, D. J., Power, R. A., Lamb, P. R., 2005, ASP Conf. Ser. 347, ADASS XIV, Eds. Shopbell, P., Britton, M. & Ebert, R. (San Francisco: Astronomical Society of the Pacific), 346
Gaede,
V., & Gunther,
O. 1998, ACM Computing Surveys, Volume 30 Number 2, 170
An error has occurred in (ref id="R2").
Variable LPAGE is undefined. [empty string]
| array
|
|---|
| 1 |
| struct |
|---|
| COLUMN |
0
|
| ID |
??
|
| LINE |
241
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:241)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 2 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
180
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 3 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
177
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 4 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
176
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 5 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
170
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 6 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
15
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 7 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
12
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 8 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
11
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 9 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
1
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 10 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
3230
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 11 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_ARTICLE
|
| LINE |
3217
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 12 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_ARTICLE
|
| LINE |
3216
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 13 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
2938
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 14 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
146
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 15 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_GENARTICLECONTENT
|
| LINE |
1
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 16 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_GENARTICLECONTENT
|
| LINE |
1
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 17 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
10
|
| RAW_TRACE |
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
|
| TEMPLATE |
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
|
| TYPE |
CFML
|
|
| 18 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
30
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 19 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
241
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 20 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
327
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 21 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
39
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 22 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_CFPAGE
|
| LINE |
634
|
| RAW_TRACE |
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
|
| TEMPLATE |
G:\www\publishha\app\PublishingApp.cfc
|
| TYPE |
CFML
|
|
| 23 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
16
|
| RAW_TRACE |
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
|
| TEMPLATE |
G:\www\publishha\app\Bootstrap.cfc
|
| TYPE |
CFML
|
|
| 24 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
18
|
| RAW_TRACE |
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
|
| TEMPLATE |
G:\www\publishha\webroot\Application.cfc
|
| TYPE |
CFML
|
|
Gray,
J., Slutz,
D., Szalay,
A. S., Thakar,
I. A., vandenBerg,
J., Kunszt,
P. Z., & Stoughton,
C. 2002, Microsoft Technical Report MSR-TR-2001-01,
An error has occurred in (ref id="R3").
Variable LPAGE is undefined. [empty string]
| array
|
|---|
| 1 |
| struct |
|---|
| COLUMN |
0
|
| ID |
??
|
| LINE |
243
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:243)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 2 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
180
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 3 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
177
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 4 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
176
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 5 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
170
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 6 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
15
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 7 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
12
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 8 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
11
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 9 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
1
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 10 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
3230
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 11 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_ARTICLE
|
| LINE |
3217
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 12 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_ARTICLE
|
| LINE |
3216
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 13 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
2938
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 14 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
146
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 15 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_GENARTICLECONTENT
|
| LINE |
1
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 16 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_GENARTICLECONTENT
|
| LINE |
1
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 17 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
10
|
| RAW_TRACE |
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
|
| TEMPLATE |
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
|
| TYPE |
CFML
|
|
| 18 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
30
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 19 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
241
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 20 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
327
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 21 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
39
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 22 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_CFPAGE
|
| LINE |
634
|
| RAW_TRACE |
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
|
| TEMPLATE |
G:\www\publishha\app\PublishingApp.cfc
|
| TYPE |
CFML
|
|
| 23 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
16
|
| RAW_TRACE |
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
|
| TEMPLATE |
G:\www\publishha\app\Bootstrap.cfc
|
| TYPE |
CFML
|
|
| 24 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
18
|
| RAW_TRACE |
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
|
| TEMPLATE |
G:\www\publishha\webroot\Application.cfc
|
| TYPE |
CFML
|
|
Gray,
J., Szalay,
A. S., Thakar,
A., Fekete,
G., O'Mullane,
W., Heber,
A., & Rots,
A. 2004, Microsoft Technical Report MSR-TR-2004-32,
An error has occurred in (ref id="R4").
Variable LPAGE is undefined. [empty string]
| array
|
|---|
| 1 |
| struct |
|---|
| COLUMN |
0
|
| ID |
??
|
| LINE |
243
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:243)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 2 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
180
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 3 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
177
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 4 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
176
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 5 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
170
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 6 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
15
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 7 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
12
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 8 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
11
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 9 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
1
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 10 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
3230
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 11 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_ARTICLE
|
| LINE |
3217
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 12 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_ARTICLE
|
| LINE |
3216
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 13 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
2938
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 14 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
146
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 15 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_GENARTICLECONTENT
|
| LINE |
1
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 16 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_GENARTICLECONTENT
|
| LINE |
1
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 17 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
10
|
| RAW_TRACE |
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
|
| TEMPLATE |
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
|
| TYPE |
CFML
|
|
| 18 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
30
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 19 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
241
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 20 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
327
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 21 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
39
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 22 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_CFPAGE
|
| LINE |
634
|
| RAW_TRACE |
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
|
| TEMPLATE |
G:\www\publishha\app\PublishingApp.cfc
|
| TYPE |
CFML
|
|
| 23 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
16
|
| RAW_TRACE |
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
|
| TEMPLATE |
G:\www\publishha\app\Bootstrap.cfc
|
| TYPE |
CFML
|
|
| 24 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
18
|
| RAW_TRACE |
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
|
| TEMPLATE |
G:\www\publishha\webroot\Application.cfc
|
| TYPE |
CFML
|
|
Hambly,
N. C., et al. 2001, MNRAS, 326, 1279
An error has occurred in (ref id="R5").
Variable LPAGE is undefined. [empty string]
| array
|
|---|
| 1 |
| struct |
|---|
| COLUMN |
0
|
| ID |
??
|
| LINE |
241
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:241)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 2 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
180
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 3 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
177
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 4 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
176
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 5 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
170
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 6 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
15
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 7 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
12
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 8 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
11
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 9 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
1
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 10 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
3230
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 11 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_ARTICLE
|
| LINE |
3217
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 12 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_ARTICLE
|
| LINE |
3216
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 13 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
2938
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 14 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
146
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 15 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_GENARTICLECONTENT
|
| LINE |
1
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 16 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_GENARTICLECONTENT
|
| LINE |
1
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 17 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
10
|
| RAW_TRACE |
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
|
| TEMPLATE |
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
|
| TYPE |
CFML
|
|
| 18 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
30
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 19 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
241
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 20 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
327
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 21 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
39
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 22 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_CFPAGE
|
| LINE |
634
|
| RAW_TRACE |
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
|
| TEMPLATE |
G:\www\publishha\app\PublishingApp.cfc
|
| TYPE |
CFML
|
|
| 23 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
16
|
| RAW_TRACE |
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
|
| TEMPLATE |
G:\www\publishha\app\Bootstrap.cfc
|
| TYPE |
CFML
|
|
| 24 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
18
|
| RAW_TRACE |
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
|
| TEMPLATE |
G:\www\publishha\webroot\Application.cfc
|
| TYPE |
CFML
|
|
Kunszt, P. Z., Szalay, A. S., Csabai, I., Thakar, A. R., 2000, ASP Conf. Ser. 216, ADASS IX, Eds. Manset, N., Veillet, C. & Crabtree, D. (San Francisco: Astronomical Society of the Pacific), 141
Monet,
D. G., et al. 2003, AJ, 125, 984
An error has occurred in (ref id="R7").
Variable LPAGE is undefined. [empty string]
| array
|
|---|
| 1 |
| struct |
|---|
| COLUMN |
0
|
| ID |
??
|
| LINE |
241
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:241)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 2 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
180
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 3 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
177
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 4 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
176
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 5 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
170
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 6 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
15
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 7 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
12
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 8 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
11
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 9 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
1
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 10 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
3230
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 11 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_ARTICLE
|
| LINE |
3217
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 12 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_ARTICLE
|
| LINE |
3216
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 13 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
2938
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 14 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
146
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 15 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_GENARTICLECONTENT
|
| LINE |
1
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 16 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_GENARTICLECONTENT
|
| LINE |
1
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 17 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
10
|
| RAW_TRACE |
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
|
| TEMPLATE |
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
|
| TYPE |
CFML
|
|
| 18 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
30
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 19 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
241
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 20 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
327
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 21 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
39
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 22 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_CFPAGE
|
| LINE |
634
|
| RAW_TRACE |
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
|
| TEMPLATE |
G:\www\publishha\app\PublishingApp.cfc
|
| TYPE |
CFML
|
|
| 23 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
16
|
| RAW_TRACE |
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
|
| TEMPLATE |
G:\www\publishha\app\Bootstrap.cfc
|
| TYPE |
CFML
|
|
| 24 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
18
|
| RAW_TRACE |
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
|
| TEMPLATE |
G:\www\publishha\webroot\Application.cfc
|
| TYPE |
CFML
|
|
Power,
R. A. 2006, CSIRO ICT Centre TR 06/209,
An error has occurred in (ref id="R8").
Variable LPAGE is undefined. [empty string]
| array
|
|---|
| 1 |
| struct |
|---|
| COLUMN |
0
|
| ID |
??
|
| LINE |
243
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:243)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 2 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
180
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 3 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
177
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 4 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
176
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 5 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
170
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 6 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
15
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 7 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
12
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 8 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
11
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 9 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
1
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 10 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
3230
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 11 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_ARTICLE
|
| LINE |
3217
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 12 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_ARTICLE
|
| LINE |
3216
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 13 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
2938
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 14 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
146
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 15 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_GENARTICLECONTENT
|
| LINE |
1
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 16 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_GENARTICLECONTENT
|
| LINE |
1
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 17 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
10
|
| RAW_TRACE |
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
|
| TEMPLATE |
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
|
| TYPE |
CFML
|
|
| 18 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
30
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 19 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
241
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 20 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
327
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 21 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
39
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 22 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_CFPAGE
|
| LINE |
634
|
| RAW_TRACE |
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
|
| TEMPLATE |
G:\www\publishha\app\PublishingApp.cfc
|
| TYPE |
CFML
|
|
| 23 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
16
|
| RAW_TRACE |
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
|
| TEMPLATE |
G:\www\publishha\app\Bootstrap.cfc
|
| TYPE |
CFML
|
|
| 24 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
18
|
| RAW_TRACE |
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
|
| TEMPLATE |
G:\www\publishha\webroot\Application.cfc
|
| TYPE |
CFML
|
|
Preparata,
F., & Shamos,
M. 1985, Computational Geometry an Introduction (NY: Springer),
An error has occurred in (ref id="R9").
Variable LPAGE is undefined. [empty string]
| array
|
|---|
| 1 |
| struct |
|---|
| COLUMN |
0
|
| ID |
??
|
| LINE |
243
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:243)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 2 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
180
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 3 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
177
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 4 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
176
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 5 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
170
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 6 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
15
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 7 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
12
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 8 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
11
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 9 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
1
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 10 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
3230
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 11 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_ARTICLE
|
| LINE |
3217
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 12 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_ARTICLE
|
| LINE |
3216
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 13 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
2938
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 14 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
146
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 15 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_GENARTICLECONTENT
|
| LINE |
1
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 16 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_GENARTICLECONTENT
|
| LINE |
1
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 17 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
10
|
| RAW_TRACE |
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
|
| TEMPLATE |
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
|
| TYPE |
CFML
|
|
| 18 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
30
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 19 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
241
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 20 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
327
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 21 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
39
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 22 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_CFPAGE
|
| LINE |
634
|
| RAW_TRACE |
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
|
| TEMPLATE |
G:\www\publishha\app\PublishingApp.cfc
|
| TYPE |
CFML
|
|
| 23 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
16
|
| RAW_TRACE |
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
|
| TEMPLATE |
G:\www\publishha\app\Bootstrap.cfc
|
| TYPE |
CFML
|
|
| 24 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
18
|
| RAW_TRACE |
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
|
| TEMPLATE |
G:\www\publishha\webroot\Application.cfc
|
| TYPE |
CFML
|
|
Skrutskie,
M. F., et al. 2006, AJ, 131, 1163
An error has occurred in (ref id="R10").
Variable LPAGE is undefined. [empty string]
| array
|
|---|
| 1 |
| struct |
|---|
| COLUMN |
0
|
| ID |
??
|
| LINE |
241
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:241)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 2 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
180
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 3 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
177
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 4 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
176
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 5 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
170
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 6 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
15
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 7 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
12
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 8 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
11
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 9 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
1
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 10 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
3230
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 11 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_ARTICLE
|
| LINE |
3217
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 12 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_ARTICLE
|
| LINE |
3216
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 13 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
2938
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 14 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
146
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 15 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_GENARTICLECONTENT
|
| LINE |
1
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 16 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_GENARTICLECONTENT
|
| LINE |
1
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 17 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
10
|
| RAW_TRACE |
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
|
| TEMPLATE |
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
|
| TYPE |
CFML
|
|
| 18 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
30
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 19 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
241
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 20 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
327
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 21 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
39
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 22 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_CFPAGE
|
| LINE |
634
|
| RAW_TRACE |
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
|
| TEMPLATE |
G:\www\publishha\app\PublishingApp.cfc
|
| TYPE |
CFML
|
|
| 23 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
16
|
| RAW_TRACE |
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
|
| TEMPLATE |
G:\www\publishha\app\Bootstrap.cfc
|
| TYPE |
CFML
|
|
| 24 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
18
|
| RAW_TRACE |
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
|
| TEMPLATE |
G:\www\publishha\webroot\Application.cfc
|
| TYPE |
CFML
|
|
Sinnott,
R. W. 1984, S&T, 68, 159
An error has occurred in (ref id="R11").
Variable LPAGE is undefined. [empty string]
| array
|
|---|
| 1 |
| struct |
|---|
| COLUMN |
0
|
| ID |
??
|
| LINE |
243
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:243)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 2 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
180
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 3 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
177
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 4 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
176
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 5 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
170
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 6 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
15
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 7 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
12
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 8 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
11
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 9 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
1
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 10 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
3230
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 11 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_ARTICLE
|
| LINE |
3217
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 12 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_ARTICLE
|
| LINE |
3216
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 13 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
2938
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 14 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
146
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 15 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_GENARTICLECONTENT
|
| LINE |
1
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 16 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_GENARTICLECONTENT
|
| LINE |
1
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 17 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
10
|
| RAW_TRACE |
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
|
| TEMPLATE |
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
|
| TYPE |
CFML
|
|
| 18 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
30
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 19 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
241
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 20 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
327
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 21 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
39
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 22 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_CFPAGE
|
| LINE |
634
|
| RAW_TRACE |
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
|
| TEMPLATE |
G:\www\publishha\app\PublishingApp.cfc
|
| TYPE |
CFML
|
|
| 23 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
16
|
| RAW_TRACE |
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
|
| TEMPLATE |
G:\www\publishha\app\Bootstrap.cfc
|
| TYPE |
CFML
|
|
| 24 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
18
|
| RAW_TRACE |
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
|
| TEMPLATE |
G:\www\publishha\webroot\Application.cfc
|
| TYPE |
CFML
|
|
Szalay,
A. S., Gray,
J., Thakar,
A., Kunszt,
P. Z., Malik,
T., Raddick,
J., Stoughton,
C., & vandenBerg,
J. 2000, ACM SIGMOD, Eds. Chen, W., Naughton, J. F., Bernstein, P. A., 451,
An error has occurred in (ref id="R12").
Variable LPAGE is undefined. [empty string]
| array
|
|---|
| 1 |
| struct |
|---|
| COLUMN |
0
|
| ID |
??
|
| LINE |
243
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor10(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:243)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 2 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
180
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor12(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:180)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 3 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
177
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor13(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:177)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 4 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
176
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor14(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:176)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 5 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
170
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor40(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:170)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 6 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
15
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor41(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:15)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 7 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
12
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor42(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:12)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 8 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
11
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986._factor43(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:11)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 9 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_INCLUDEJOURNALREF_B
|
| LINE |
1
|
| RAW_TRACE |
at cfincludeJournalRef_B2ecfm1510229986.runPage(G:\www\publishha\app\views\journal\includeJournalRef_B.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\includeJournalRef_B.cfm
|
| TYPE |
CFML
|
|
| 10 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
3230
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor150(G:\www\publishha\app\modules\journal\Article.cfc:3230)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 11 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_ARTICLE
|
| LINE |
3217
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1._factor151(G:\www\publishha\app\modules\journal\Article.cfc:3217)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 12 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_ARTICLE
|
| LINE |
3216
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcREFERENCESDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:3216)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 13 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
2938
|
| RAW_TRACE |
at cfArticle2ecfc1291681887$funcBACKSECTIONSDTD1.runFunction(G:\www\publishha\app\modules\journal\Article.cfc:2938)
|
| TEMPLATE |
G:\www\publishha\app\modules\journal\Article.cfc
|
| TYPE |
CFML
|
|
| 14 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
146
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447._factor5(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:146)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 15 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_GENARTICLECONTENT
|
| LINE |
1
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447._factor6(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 16 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_GENARTICLECONTENT
|
| LINE |
1
|
| RAW_TRACE |
at cfgenArticleContent2ecfm782833447.runPage(G:\www\publishha\app\views\journal\generator\genArticleContent.cfm:1)
|
| TEMPLATE |
G:\www\publishha\app\views\journal\generator\genArticleContent.cfm
|
| TYPE |
CFML
|
|
| 17 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
10
|
| RAW_TRACE |
at cfStaticPageLayout2ecfm1426351739.runPage(G:\www\publishha\app\views\layout\StaticPageLayout.cfm:10)
|
| TEMPLATE |
G:\www\publishha\app\views\layout\StaticPageLayout.cfm
|
| TYPE |
CFML
|
|
| 18 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CFINCLUDE
|
| LINE |
30
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcRENDERLAYOUT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:30)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 19 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
241
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENARTICLECONTENT.runFunction(G:\www\publishha\app\controller\CacheController.cfc:241)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 20 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
327
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENARTICLE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:327)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 21 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_UDFMETHOD
|
| LINE |
39
|
| RAW_TRACE |
at cfCacheController2ecfc639388092$funcGENCACHE.runFunction(G:\www\publishha\app\controller\CacheController.cfc:39)
|
| TEMPLATE |
G:\www\publishha\app\controller\CacheController.cfc
|
| TYPE |
CFML
|
|
| 22 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_CFPAGE
|
| LINE |
634
|
| RAW_TRACE |
at cfPublishingApp2ecfc536529069$funcPROCESSREQUEST.runFunction(G:\www\publishha\app\PublishingApp.cfc:634)
|
| TEMPLATE |
G:\www\publishha\app\PublishingApp.cfc
|
| TYPE |
CFML
|
|
| 23 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
16
|
| RAW_TRACE |
at cfBootstrap2ecfc660975501$funcHANDLEREQUEST.runFunction(G:\www\publishha\app\Bootstrap.cfc:16)
|
| TEMPLATE |
G:\www\publishha\app\Bootstrap.cfc
|
| TYPE |
CFML
|
|
| 24 |
| struct |
|---|
| COLUMN |
0
|
| ID |
CF_TEMPLATEPROXY
|
| LINE |
18
|
| RAW_TRACE |
at cfApplication2ecfc757760907$funcONREQUESTSTART.runFunction(G:\www\publishha\webroot\Application.cfc:18)
|
| TEMPLATE |
G:\www\publishha\webroot\Application.cfc
|
| TYPE |
CFML
|
|
1 www.mso.anu.edu.au/skymapper/ 2 www.star.le.ac.uk/~cgp/ag/skyindex.html 3 www.opengeospatial.org/ 4 openskyquery.net/Sky/skysite/ 5 www.mysql.com 6 www.oracle.com 7 tdc-www.harvard.edu/wcstools/