Comparison of artificial absorbing boundaries for acoustic wave equation modelling
Yingjie Gao 1 2 Hanjie Song 1 2 Jinhai Zhang 1 3 Zhenxing Yao 11 Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China.
2 University of Chinese Academy of Sciences, Beijing 100049, China.
3 Corresponding author. Email: zjh@mail.iggcas.ac.cn
Exploration Geophysics 48(1) 76-93 https://doi.org/10.1071/EG15068
Submitted: 17 July 2015 Accepted: 22 November 2015 Published: 23 December 2015
Journal Compilation © ASEG 2017 Open Access CC BY-NC-ND
Abstract
Absorbing boundary conditions are necessary in numerical simulation for reducing the artificial reflections from model boundaries. In this paper, we overview the most important and typical absorbing boundary conditions developed throughout history. We first derive the wave equations of similar methods in unified forms; then, we compare their absorbing performance via theoretical analyses and numerical experiments. The Higdon boundary condition is shown to be the best one among the three main absorbing boundary conditions that are based on a one-way wave equation. The Clayton and Engquist boundary is a special case of the Higdon boundary but has difficulty in dealing with the corner points in implementaion. The Reynolds boundary does not have this problem but its absorbing performance is the poorest among these three methods. The sponge boundary has difficulties in determining the optimal parameters in advance and too many layers are required to achieve a good enough absorbing performance. The hybrid absorbing boundary condition (hybrid ABC) has a better absorbing performance than the Higdon boundary does; however, it is still less efficient for absorbing nearly grazing waves since it is based on the one-way wave equation. In contrast, the perfectly matched layer (PML) can perform much better using a few layers. For example, the 10-layer PML would perform well for absorbing most reflected waves except the nearly grazing incident waves. The 20-layer PML is suggested for most practical applications. For nearly grazing incident waves, convolutional PML shows superiority over the PML when the source is close to the boundary for large-scale models. The Higdon boundary and hybrid ABC are preferred when the computational cost is high and high-level absorbing performance is not required, such as migration and migration velocity analyses, since they are not as sensitive to the amplitude errors as the full waveform inversion.
Key words: absorbing boundary condition, Higdon boundary, hybrid ABC, perfectly matched layer, sponge boundary.
Introduction
Numerical modelling of seismic wavefields is important for understanding wave phenomena in complex media and is essential for full waveform inversion. Due to the restrictions on both memory requirement and computational cost, the model has to be limited in size and focused on the area of interest by introducing artificial boundaries. Therefore, an artificial boundary condition is needed to absorb the energy of the reflections from these artificial boundaries. Two main kinds of solutions have been proposed for this purpose: absorbing boundary conditions (ABCs) (e.g. Clayton and Engquist, 1977; Reynolds, 1978; Liao et al., 1984; Higdon, 1986; Higdon, 1991) and absorbing boundary layers (e.g. Cerjan et al., 1985; Kosloff and Kosloff, 1986; Compani-Tabrizi, 1986, Sochacki et al., 1987; Bérenger, 1994; Komatitsch and Martin, 2007; Liu and Sen, 2010, 2012).
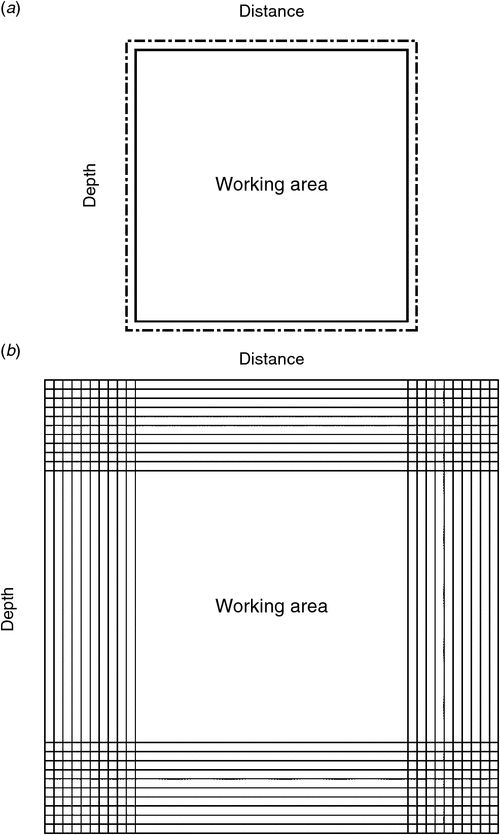
The ABC splits the wave equation into two directions: inside and outside equations using the one-way wave equation method (Claerbout, 1985); then, only the outside equation is used on one or two layers outside of the interested area to avoid reflections inwards (as shown in Figure 1a). The ABC has a good performance when the incident waves are propagating within a certain angle range, especially when the incident waves are close to the direction normal to the boundary. When the incident angle is large (say 60° away from the direction normal to the boundary), the energy of artificial reflections would be boosted because the accuracy of both travel time and amplitude calculated with the one-way wave equation at wide angles is low.
|
The ABC has been popular since the early 1970s, and some of the classical ABCs can be defined up to any desired order; however, the appearance of increasingly high-order derivatives in these ABCs renders them impractical beyond a certain order, typically 2 or 3. For example, the m-order Higdon boundary involves m-order derivatives both in space and time, and is thus very inconvenient for implementation when m is large (Bécache et al., 2010). Collino (1993) devised a new scheme for high-order ABCs by using special auxiliary variables. This scheme is based on a reformulation of the sequence of ABC that was proposed by Higdon (1986). In contrast to the original formulation of the Higdon conditions, this scheme does not involve any high derivatives beyond the second order by introducing special auxiliary variables. As a result, this scheme can be easily used up to any desired order m. Moreover, the computational cost only increases linearly with m (Givoli and Neta, 2003; Givoli, 2004). Corner compatibility conditions are derived for high-order radiation boundary conditions using auxiliary variable equations (Hagstrom and Warburton, 2004; Bécache et al., 2010).
The absorbing boundary layers use many layers to attenuate the artificial reflections gradually; thus, we can greatly reduce artificial reflections with an adequate number of layers (as shown in Figure 1b). There are three kinds of absorbing boundary layers: the sponge boundary (e.g. Cerjan et al., 1985; Compani-Tabrizi, 1986; Kosloff and Kosloff, 1986; Sochacki et al., 1987), the perfectly matched layer (PML) (e.g. Bérenger, 1994; Chew and Liu, 1996; Hastings et al., 1996; Collino and Tsogka, 2001; Marcinkovich and Olsen, 2003; Wang and Tang, 2003), and the hybrid absorbing boundary condition (Liu and Sen, 2010, 2012).
The sponge boundary (e.g. Cerjan et al., 1985; Compani-Tabrizi, 1986; Kosloff and Kosloff, 1986; Sochacki et al., 1987) is composed of dozens of layers outside the interested area. The sponge boundary introduced by Cerjan et al. (1985) avoids apparent inwards reflections by directly attenuating the wavefield with a gradually enhanced attenuation factor from inner to outer of the damping boundary belt. This method is simple in numerical implementation since there is no need to modify the wave equations. Sochacki et al. (1987) implemented the attenuation of seismic waves in the sponge boundary by introducing attenuation term directly to the wave equation. Zhou (1988) pointed out that a careful selection of the width of the damping boundary belt and attenuation factor is essential for the success of reducing the artificial reflections. However, no perfect rule for the selection has been available until now and one has to choose optimal parameters via numerical tests before it is ready for practical applications.
The PML (Bérenger, 1994) applies a completely new mechanism to avoid apparent artificial reflections. The PML introduces physical attenuations to the wave equation. The PML modifies the partial derivatives in the wave equation using complex coordinate stretching by introducing an imaginary part associated with an attenuation factor. Complex coordinate stretching is well known for viscoelastic media to understand the nature of the intrinsic attenuation for wave propagation; thus, the PML presents a nice rule in designing the optimal attenuation coefficients by tuning the attenuation factor. Rabinovich et al. (2010) compared high-order ABC with the PML in the frequency domain.
Although the traditional PML has been widely used in seismic wave simulations, it produces apparent artificial reflections for nearly grazing incident waves, low-frequency waves, and evanescent waves (e.g. Festa and Vilotte, 2005; Komatitsch and Martin, 2007; Drossaert and Giannopoulos, 2007a). Complex frequency-shifted PML (Kuzuoglu and Mittra, 1996) has a better absorbing performance in these cases (e.g. Festa et al., 2005; Festa and Vilotte, 2005; Drossaert and Giannopoulos, 2007a, 2007b; Komatitsch and Martin, 2007). In addition, the traditional PML adopts a non-physical splitting of wave equations, which has been proved to be weakly well posed (Abarbanel and Gottlieb, 1997). Thus, the convolutional PML is proposed to overcome this problem (e.g. Roden and Gedney, 2000; Komatitsch and Martin, 2007). Roden and Gedney (2000) further derived a non-split wavefield of convolutional complex frequency-shifted PML (CPML) that can be efficiently calculated with recursive convolution algorithm (Luebbers and Hunsberger, 1992). Kristek et al. (2009) discussed the split/unsplit, classical/convolutional and general/special PML formulations in detail, which can help the reader understand the classification of different PML formulations.
Recently, the PML with auxiliary differential equations (ADE-PML) has been proposed (e.g. Gedney and Zhao, 2010; Martin et al., 2010; Zhang and Shen, 2010). Both CPML and ADE-PML can be implemented for complex frequency-shifted operators, but the ADE form allows for extension to higher order time schemes and is also easier to implement for avoiding the convolutional calculation. Xie et al. (2014) gave a thorough review on the development from PML to ADE-PML.
Liu and Sen (2010, 2012) proposed a hybrid ABC. They split the model into three parts: the working area, the transition area and the ABC. The wavefields within the transition area are averaged by a linear weighting function between the wavefields generated by a two-way wave equation (i.e. acoustic wave equation) and one-way wave equation. The transition area smoothly absorbs the wavefields that propagate outside the working area and thus can decrease the boundary reflections. The hybrid ABC performs better than either the pure ABC or pure sponge boundary.
In the field of seismic exploration, artificial boundary conditions are becoming more and more important with an increasing demand on both the accuracy and computational efficiency of the migration and inversion, especially for large-scale 3D complex models. We need to further reduce computational cost and memory demands for the artificial boundary conditions. However, various artificial boundary conditions arise in history; thus, it is not so easy to be familiar with all of them, although this is necessary for further improvement towards much faster and smarter absorbing boundary conditions.
In this paper, we provide a thorough review of all typical absorbing boundary conditions and derive their equations in a uniform mathematical form. Then, we reveal the fundamental similarities and differences between similar methods through theoretical analyses. Next, we examine the performance of these boundary conditions via numerical experiments and qualitatively show their advantages and disadvantages. Finally, we summarise their applicable conditions and give some comprehensive suggestions on choosing different boundary conditions for practical applications.
Absorbing boundary conditions
Clayton and Engquist boundary
Engquist and Majda (1977) discussed absorbing boundary conditions for a general class of differential equations based on pseudo-differential operators. Clayton and Engquist (1977) derived the absorbing boundary condition applicable to both acoustic and elastic wave equations by the approximation of a one-way wave equation. Engquist and Majda (1979) tried to solve the stability problem at the corners. Here we call this method the Clayton and Engquist boundary.
For a medium of the form D = {(x, z, t)|−a ≤ x ≤ a, −b ≤ z ≤ b}, a 2D scalar wave equation can be expressed as

We apply the Fourier transform on both temporal and spatial variables to Equation 1, and the dispersion relation can be obtained as follows

where kx and kz are the horizontal and vertical wavenumbers, respectively; ω is the circular frequency, p is the displacement, v is the velocity of the acoustic wave propagating in the media. According to the one-way wave equation theory (Claerbout, 1985), we can obtain the square-root operator along x-direction as follows

where ± represents a plane wave propagating along the positive or negative x-axis, respectively. The one-way wave equation method can separate the incoming and outgoing wavefields around the boundaries. For the positive x-axis at the right boundary, we have

which is the dispersion relation of the one-way wave equation that controls the wave propagations outwards. The one-way wave equation is solved iteratively along spatial directions; thus, only the wavefield on the previous one or two layers are needed to generate the wavefield in the current layer. In other words, wavefields beyond the boundary are not needed, which means no boundary reflection occurs at the outer layer (i.e. the right boundary).
Taylor-series expansion of the square-root operator on the right side of Equation 4 leads to unstable differencing schemes (Engquist and Majda, 1977); thus, Clayton and Engquist (1977) expanded this operator by Padé approximation. The first three orders are as follows (Clayton and Engquist, 1977):


and

The recurrence relation for the above approximations is

where a1 = 1.
Equations 6 and 7 are widely used in designing one-way wave equation migration algorithms (Claerbout, 1985). The differential formats corresponding to Equations 5–7 are as follows (Clayton and Engquist, 1977)


and

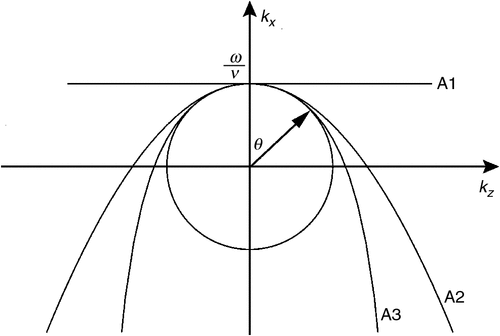
where A1, A2, and A3 are right absorbing boundary conditions using the first, second and third order paraxial approximation, respectively. The accuracy analyses of these three approximations are shown in Figure 2, compared with the analytical solution. Obviously, high orders have better accuracy than lower orders do. But the error of the third order is still apparent for wide angles away from the normal direction to the boundary. On the other hand, it is a little difficult to solve the third order approximation shown in A3; in contrast, A1 is simple in implementation but its accuracy is too low. Therefore, A2 is a reasonable trade-off and is widely used. The differential equations for A2 on the left, upper and bottom boundaries are as follows (Clayton and Engquist, 1977):
|

The Clayton and Engquist boundary needs the value of wavefields both along x-axis and z-axis; thus, the corners would act as point sources and cause instabilities (Engquist and Majda, 1979). Therefore, special treatments are needed at the corners for high-order Clayton and Engquist boundary conditions. One can replace A2 with A1 at the corners by assuming that the incident angle is 45° at the corners to avoid numerical instabilities (Clayton and Engquist, 1977; Engquist and Majda, 1979). For example, the differential formula for the lower right-hand corner becomes (Clayton and Engquist, 1977)

Similarly, the other three corners for the absorbing boundary conditions are expressed as
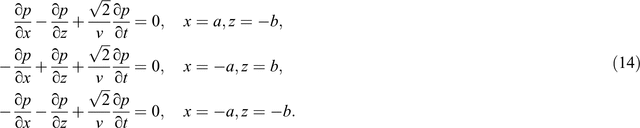
According to the plane wave solutions of the wave equation, plane waves spread to the right boundary can be written as

where θ is the incident angle, namely the included angle between the wavefront and the x-axis; kx and kz are the wavenumbers along x-axis and z-axis, respectively; and k is the wavenumber along the incident angle. Similarly, the reflected wave can be expressed as

where r is the reflection coefficient. The total wavefields around the boundary are
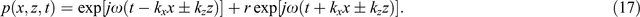
Taking Equation 17 into the right boundary conditions, we can obtain the reflection coefficient (Clayton and Engquist, 1977) as

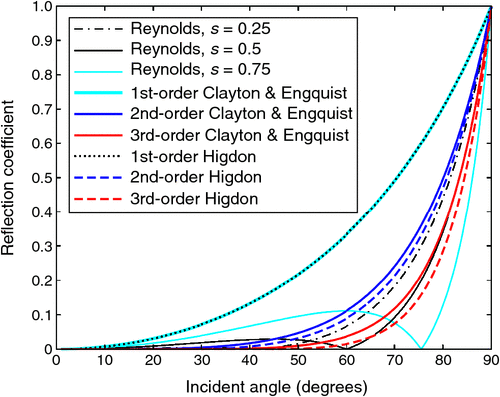
where j = 1, 2, 3 represents the first, second and third order paraxial approximation, respectively; and θ is the incident angle. Figure 3 shows the absolute value of the reflection coefficient versus incident angle for different orders of the Clayton and Engquist boundaries.
|
Reynolds boundary
Reynolds (1978) derived another absorbing boundary condition based on the one-way wave equation, which is known as the transparent boundary condition. Here we call it the Reynolds boundary. The wave Equation 1 can be rewritten as follows:
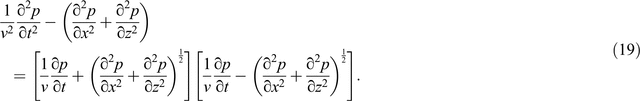
Denoting

Equation 19 becomes
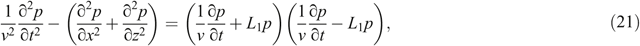
where 1/v ∂p/∂t + L1p = 0 corresponds to the right boundary, and 1/v ∂p/∂t−L1p = 0 corresponds to the left boundary. Using Taylor-series expansion L1 can be approximated as follows:

Thus, on the right boundary we have

Substituting

into Equation 23, we obtain

Equation 25 is the expression of the Reynolds boundary on the right side.
Considering the stability condition of the finite-difference method, we can replace the coefficient of ∂2p/∂z2 in Equation 23 by s/(1+s), where s = vΔt/Δx, Δt is the temporal interval, and Δx is the spatial interval in x-direction; thus, Equation 23 becomes (Reynolds, 1978)

which can be rearranged as

Obviously, Equation 23 is the special case when s = vΔt/Δx = 1.
Similarly, the Reynolds boundaries on the left, upper, and bottom boundaries are as follows (Reynolds, 1978):
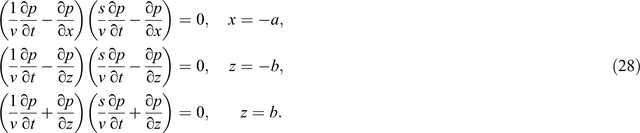
Taking the right boundary as an example, we substitute Equation 17 into Equation 26 and obtain
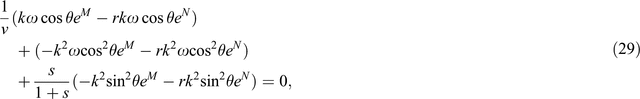
where θ is the incident angle, M = j(ωt−kx cos θ±kz sin θ), and N = j(ωt + kx cos θ ± kz sin θ). Thus, the reflection coefficient of the Reynolds boundary versus the incident angle is (Reynolds, 1978)

Figure 3 shows the absolute value of the reflection coefficient versus incident angle using different s for the Reynolds boundary.
Higdon boundary
Bayliss and Turkel (1980) proposed an absorbing boundary condition in the spherical coordinate system. Higdon (1986) further derived a progressive absorbing boundary equation in the Cartesian coordinate system (Higdon, 1986, 1987, 1990, 1991). We call this absorbing boundary condition the Higdon boundary for simplicity. Peng and Toksöz (1995) optimised the coefficients to improve the absorbing performance.
Plane waves spread to the right boundary can be written as Equation 15, which also satisfies the boundary condition

Equation 31 can be regarded as a compatibility condition for Equation 15, and it can annihilate waves moving at angles of incidence ±θ. In particular, the boundary condition ∂p/∂x + 1/v ∂p/∂t = 0 is compatible with outgoing waves moving at normal incidence, which is the first-order Clayton and Engquist boundary. Similarly, a linear combination of plane waves moving outward at angles ±θ1,…, ±θm would exactly satisfy the high-order versions (Higdon, 1986)
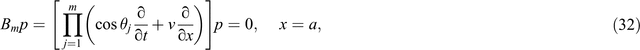
where m is the order of the absorbing boundary condition, and θj is the angular parameter that can be chosen. Higdon (1986) demonstrated that the application of Equation 32 as the absorbing boundary can completely absorb the incident waves along the incident angle ±θj in theory.
Higdon (1991) pointed out that the angle θj can be chosen to take advantage of a priori information about the direction that along which waves are expected to approach the boundary. For example, if waves near normal incidence are of greatest importance, then we use θj = 0 for all j. If a wide range of incident angles presents, then it may be advisable to move θj away from 0° so as to distribute the roots of the reflection coefficient at a broad range of angles. In general, the optimal choice of θj is problem dependent. We use θ1 = 0 and θ2 = π/6 as the angle parameters for the second-order Higdon boundary in this paper.
Similarly, we can get the equations on the left, upper, and bottom boundaries as follows (Higdon, 1991):
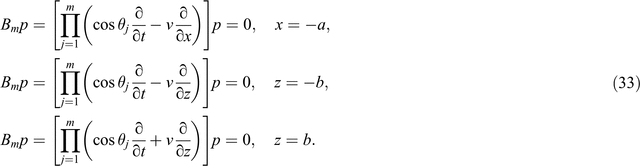
When m = 1, 2, 3, Equation 32 can be written as follows (Higdon, 1991)

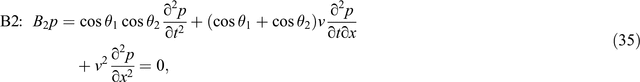
and
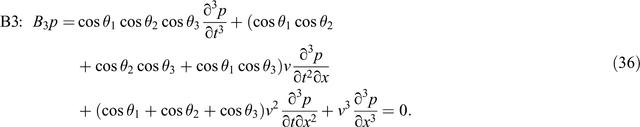
B1, B2 and B3 are the first, second and third order Higdon boundaries on the right side, respectively. Similar to the Clayton and Engquist boundary, it is complex to solve B3 but B1 is too simple; thus, B2 is preferred for practical applications. Substituting Equation 17 into Equation 32, we obtain the reflection coefficient of the Higdon boundary (Higdon, 1986)

where θ is the incident angle, and θj is a preferred incident angle that hopes to be perfectly absorbed. Figure 3 shows the absolute value of the reflection coefficient of the Higdon boundary versus angles for different orders.
For the right boundary of the second-order Higdon boundary, the differential operator form of Equation 32 when m = 2 is as follows (Higdon, 1987; Sun, 2003)
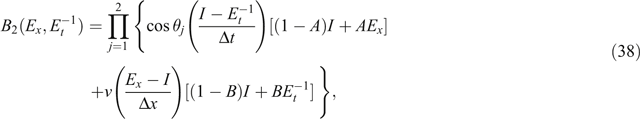
where I is the unit operator, which satisfies ExI = Ex and AI = A; A and B are the control parameters for the finite-difference scheme. Differential operator expressions on space and time are as follows:

where i and j are indices of spatial grids along x- and z-directions, respectively; and k is the index of temporary grids.
Equation 38 includes three type of finite-difference schemes: the forward Euler when A = 0, B = 1, the backward Euler when A = 0, B = 0, and the box scheme when A = 0.5, B = 0.5. We use the forward Euler difference scheme in this paper. For more details of other cases, readers can refer to Higdon (1987).
Relationship between Reynolds boundary, Clayton and Engquist boundary and Higdon boundary
Relationship between the Reynolds boundary and the Clayton and Engquist boundary
Equation 25 is the Reynolds boundary on the right side, under the special case when s = vΔt/Δx = 1. Equation 10 is the second-order Clayton and Engquist boundary on the right side. According to Equation 1, we replace ∂2p/∂z2 in Equation 10 by 1/v2∂2p/∂t2 − ∂2p/∂x2 and obtain

We see that Equation 40 is exactly the same as Equation 25; thus, the second-order Clayton and Engquist boundary is the special case when s = vΔt/Δx = 1 of the Reynolds boundary.
As shown in Figure 3, when the incident angle is less than 45°, the absolute value of the reflection coefficient of the second-order Clayton and Engquist boundary is less than that of the Reynolds boundary for s = 0.25 and s = 0.5, but the absolute value of the reflection coefficient of the Reynolds boundary is large when s = 0.75. From 45° to 60°, the absolute value of the reflection coefficient of the second-order Clayton and Engquist boundary is less than that of the Reynolds boundary when s = 0.25 but larger when s = 0.5 and s = 0.75. When the incident angle is greater than 60°, the absolute value of the reflection coefficient of the second-order Clayton and Engquist boundary is larger than those of the Reynolds boundaries.
At the four corner points, high-order (from the second-order) Clayton and Engquist boundaries need special treatments, which are derived by assuming that the incident angle is 45°. However, in actual simulation, especially for media with complex structures, we do not know the exact direction of the incident wave; thus, the Clayton and Engquist boundary would encounter strong reflections from corners when incident waves are far away from 45°. In contrast, the Reynolds boundary does not need any special treatment at corner points and is more straightforward in implementation.
Relationship between Clayton and Engquist boundary and Higdon boundary
From Equations 9–11, and Equations 34–36, we see that A1 and B1 are the same when cosθ1 = 1; A2 and B2 are the same when cosθ1 = cosθ2 = 1; A3 and B3 are the same when cosθ1 = cosθ2 = cosθ3 = 1. Therefore, the Clayton and Engquist boundary is the special case of the Higdon boundary when the incident angle used is equal to 0°.
As shown in Figure 3, the absolute value of the reflection coefficient of the first-order Higdon boundary is exactly the same as that of the first-order Clayton and Engquist boundary. The second-order Higdon boundary always has a smaller absolute value for the reflection coefficient than the second-order Clayton and Engquist boundary does. Similarly, the third order Higdon boundary always has smaller absolute value of the reflection coefficient than the third order Clayton and Engquist boundary does.
For the second-order boundary, the Reynolds boundary seems to have much smaller absolute value of the reflection coefficient, ~60° compared to both the Clayton and Engquist boundary and the Higdon boundary; however, its absolute value of the reflection coefficient is much bigger than the latter, between 20° to 40°. This means that the actual performance of the Reynolds boundary would not be as good as that of the other two methods.
Absorbing boundary layers
Cerjan sponge boundary
Cerjan et al. (1985) proposed to eliminate the reflected wave by setting the damping boundary with multilayers outside the working area. An outward decaying exponential function can effectively reduce incident waves. In each time step of the wavefield extrapolation, the amplitude of the seismic wave on each grid within the absorption area is decayed by the Gauss function (Cerjan et al., 1985)
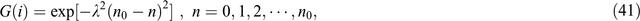
where λ is the attenuation coefficient, n is the grid index of the damping area, and n0 is the layer number of the damping area (i.e. the index of the outer most layer). Cerjan et al. (1985) gave a set of empirical parameters n0 = 20 and λ = 0.015 through numerical experiments. Bording (2004) pointed out that these parameters are not optimised and suggested a group of optimised parameters n0 = 45 and λ = 0.0053.
Sochacki sponge boundary
Cerjan et al. (1985) showed that decaying the amplitudes of the waves by multiplying by an exponential function in a region surrounding the model can considerably reduce reflections for waves at any angle of incidence. Their method, however, acts on discrete numerical solutions rather than on the wave equation. Sochacki et al. (1987) implemented the attenuation of seismic waves in the sponge boundary by introducing an attenuation term directly to the wave equation. The wave equation is extended as (Sochacki et al., 1987)

where A(x, z) is the attenuation function. In the working area, A(x, z) = 0; in the damping area, Sochacki et al. (1987) suggested five kinds of damper as follows:
1. Linear damper (Sochacki et al., 1987)

where α = S/MxNz, x1 = x0 + Δx, z1 = z0 + Δz, Mx is the length of attenuation zone along the x-direction, Nz is the length of the attenuation zone along the z-direction, and S = ‖‖ A ‖‖∞ = max{A(x, z)};
2. Exponent damper (Sochacki et al., 1987)

where β = lnS/[lnMxNz−lnΔxΔz], and α = (ΔxΔz)−β;
3. Cubic damper (Sochacki et al., 1987)

where α = S/(MxNz)3;
4. Exponential damper (Sochacki et al., 1987)

where β = ln S/[(Mx−Δx)(Nz−Δz)], and α = exp(−βΔxΔz);
5. Gaussian damper (Sochacki et al., 1987)

where β = {(Δx+Δz)(Mx + Nz)/[(Mx + Nz)−(Δx+Δz)]}ln S, and α = exp[−β/(Δx + Δz)].
Compared with the Cerjan sponge boundary, the Sochacki sponge boundary has the following advantages: first, the damping term has a physical meaning and can be used to study the effects of friction and other dissipative phenomena on acoustic and elastic waves; second, it is easier to determine the reflection coefficient; third, since the damping term is part of the wave equation, a variety of numerical techniques can be used and theoretical results are more easily obtained.
Perfectly matched layer
Bérenger (1994) introduced a completely new boundary condition called the perfectly matched layer (PML). The PML has a remarkable property of having a zero reflection coefficient for all incident angles and all frequencies for the continuous wave equation. The PML shows great superiority over the classical boundary conditions mentioned above and is widely used in acoustic wave simulations (e.g. Abarbanel and Gottlieb, 1997; Liu and Tao, 1997; Qi and Geers, 1998; Liu, 1999; Katsibas and Antonopoulos, 2002; Diaz and Joly, 2006; Bermúdez et al., 2007) and elastic wave simulations (e.g. Chew and Liu, 1996; Hastings et al., 1996; Collino and Tsogka, 2001; Festa and Nielsen, 2003; Komatitsch and Tromp, 2003; Basu and Chopra, 2004; Festa et al., 2005, Festa and Vilotte, 2005; Appelö and Kreiss, 2006; Komatitsch and Martin, 2007; Yang et al., 2007; Lan et al., 2013). The PML has been further extended to other methods, such as the pseudo-spectral method (Liu, 1998), the finite element method (Collino and Tsogka, 2001), the spectral element method (Festa and Vilotte, 2005), and the grid method (Xu and Zhang, 2008).
The 2D scalar wave equation shown in Equation 1 can be rewritten as (Liu and Tao, 1997; Hustedt et al., 2004)

After transforming into the frequency domain by the Fourier transform, Equation 48 becomes

where Px, Pz, P, 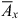 , and
, and 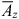 are the Fourier transforms of Px, Pz, p, Ax and Az, respectively.
are the Fourier transforms of Px, Pz, p, Ax and Az, respectively.
The essence of the PML is to replace propagating (oscillating) waves with exponentially decaying waves by analytically continuing the wave equation into complex coordinates (e.g. Bérenger, 1994; Collino and Tsogka, 2001; Nataf, 2013) using

where dx (x) is the attenuation coefficients in x-direction, which can be obtained by (Collino and Tsogka, 2001)

where vmax is the maximum acoustic wave velocity, δ is the thickness of the PML area, and R is the theoretical reflection coefficient. We use R = 10−5 when δ = 10Δx, and R = 10−7 when δ = 20Δx.
Substituting Equation 50 into Equation 49, we obtain

After rearranging Equation 52, we have

Finally, the acoustic wave equation with PML can be expressed as (Liu and Tao, 1997)

Convolutional perfectly matched layer
The wave equation is extended to complex coordinates by (Komatitsch and Martin, 2007)

where αx = αmax(1−x/δ), αmax = πf0, f0 is the dominant frequency of the source, and χx = 1 + (χmax −1) (x/δ)2. Generally χx = 1 is good enough for most applications (Komatitsch and Martin, 2007). Thus, we can obtain
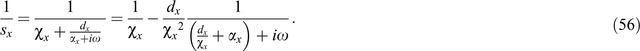
On the assumption that 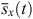 is the inverse Fourier transform of 1/sx about ω, we have
is the inverse Fourier transform of 1/sx about ω, we have

Denoting

we obtain

In the time domain, we have

where 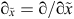 and ∂x = ∂/∂x. At the nth time step, the convolutional term in Equation 60 can be written as
and ∂x = ∂/∂x. At the nth time step, the convolutional term in Equation 60 can be written as

The integral in Equation 61 is written as a discrete form:

Using Equations 61 and 62, we obtain
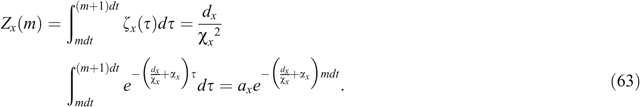
Let bx = exp[ −(dx/χx + αx)mdt], ax = (bx −1)dx/[χx(dx + χx αx)]. Using the recursive convolution algorithm deduced by Luebbers and Hunsberger (1992), we have

thus,

Pasalic and McGarry (2010) gave a detailed derivation of CPML for the second-order acoustic wave equation. Introducing new auxiliary variables φx and φz, we can rewrite the second-order spatial derivatives in terms of the first-order derivatives as (Pasalic and McGarry, 2010)
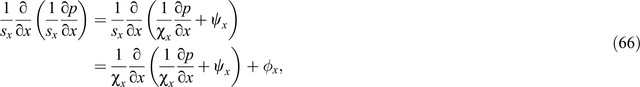
where

The CPML implementation for the acoustic wave equation is expressed as (Pasalic and McGarry, 2010)

Hybrid ABC
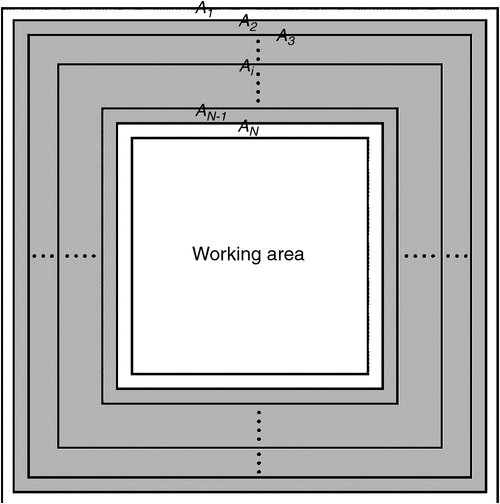
Liu and Sen (2010, 2012) proposed an efficient hybrid ABC to absorb boundary reflections. The transition area is added between the working area and the model boundary. Figure 4 shows the sketch map of the hybrid ABC. The wavefields in the transition area (grey area in Figure 4) are weighted between two-way wavefields and one-way wavefields, where the one-way wavefields are calculated by the second-order Higdon boundary. A linear weighting function is used to sum the wavefields (Liu and Sen, 2010, 2012).
|

where ptwo are the two-way wavefields, pone are the one-way wavefields, wAi = (i−1)/N, and N is the number of layers used in the hybrid ABC.
Numerical experiments
Square model
We perform numerical experiments on a homogeneous medium. The wave velocity of a square model is 2500 m/s. The spatial grid interval is 5 m, and the grid number is 301 × 301. The source is a Ricker wavelet with a dominant frequency of 20 Hz. We compare the boundary reflections using various boundary conditions: the second-order Clayton and Engquist boundary; the second-order Higdon boundary; the Reynolds boundary; the Cerjan sponge boundary (with 20 absorbing layers) (using parameters given by Cerjan et al., 1985); the Sochacki sponge boundary (20 layers) (using the linear damper given by Sochacki et al., 1987); the hybrid ABC (10 layers and 20 layers); the PML (10 layers and 20 layers); and the CPML (10 layers and 20 layers).
Artificial absorbing boundary conditions are used on all boundaries of the model. We perform 12 sets of experiments to compare the reflections of several absorbing boundary conditions. We use a very large model to simulate the theoretical wavefield to avoid boundary reflections, which can be regarded as a reference to check the performance of the artificial absorbing boundary conditions.
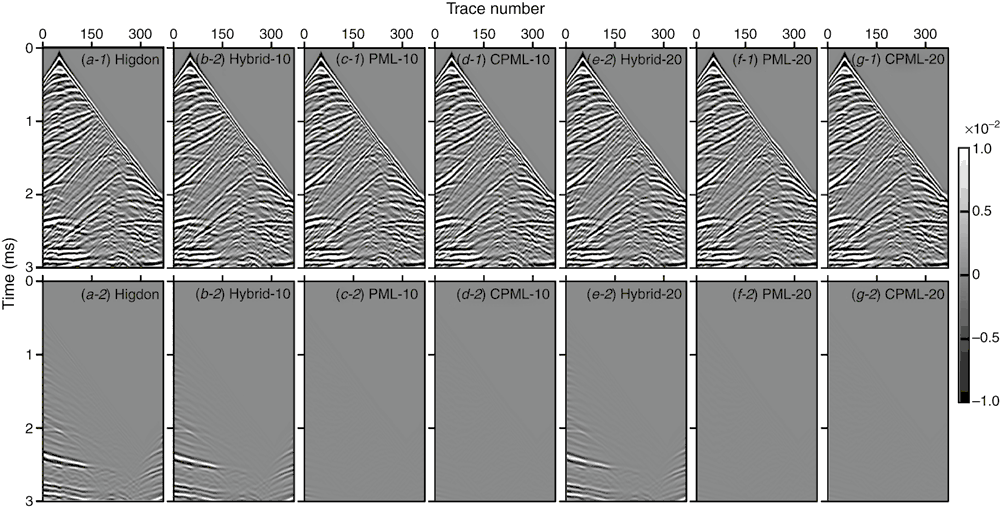
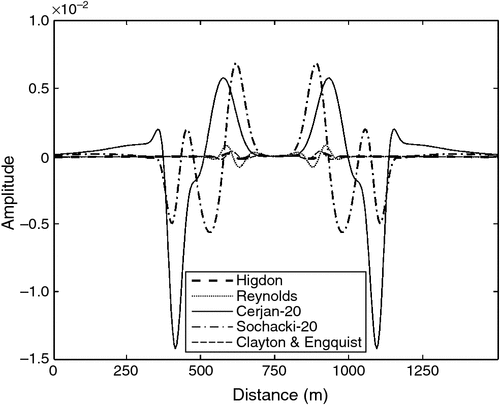
Figures 5 and 6 show the snapshots obtained by different boundary conditions. Figures 7 and 8 show the waveforms obtained by different boundary conditions. Figure 9 shows the wavefield records obtained on the ground surface (i.e. 0 m in depth). The maximum value of the wavefield records is 0.1294. Among the three ABC, the absorption performance of the Clayton and Engquist boundary is better than that of the Reynolds boundary, and the absorption performance of the Higdon boundary is the best. The hybrid ABC (Liu and Sen, 2010, 2012) is shown to be superior to the Higdon boundary. Compared with the PML and CPML, however, absorption performance of the hybrid ABC is relatively poor. In terms of the computational cost, at least, the Higdon boundary is superior to the absorbing layers (i.e. hybrid ABC, PML, CPML or sponge boundary) since only one or two layers are involved in the computations. Therefore, the Higdon boundary would be a good candidate when the demand of absorbing performance is not so serious but the computational cost is heavy.
|
|
The absorption performance of the sponge boundary is not as good as that of the PML method and even poorer than that of the Higdon boundary. Of course, the absorption performance of the sponge boundary may be improved after some careful tests and selections on the parameters (e.g. tuning the thickness of the damping belt and the attenuation coefficients). Nevertheless, our numerical results shown here reveal that the sponge boundary would have potential risks, and further research is still needed for reliable or universally optimal parameters.
As shown in Figure 8, the 20-layer PML (or CPML) performs better than the 10-layer one does, since the former has almost no visible boundary reflections. In addition, the 10-layer PML has smaller artificial reflections than the 20-layer hybrid ABC does. This indicates that the PML is superior to the hybrid ABC with the same number of absorbing layers.
Long model
In practical applications, our model is sometimes very large in scale, which would lead to a nearly grazing incidence when the wavefields are propagating far away from the source. We further examine various absorbing boundary conditions for a large-scale long model. The grid number is 601 × 61. The seismic source is located at 2500 m along x-direction and 50 m in depth. The other parameters are the same as the square model. Seven boundary conditions are compared: the second-order Higdon boundary, the hybrid ABC (with 10 and 20 absorbing layers), the PML (10 and 20 layers) and the CPML (10 and 20 layers). We use a much larger scale model to generate an artificial-reflection free case as the reference for checking the absorbing performance.
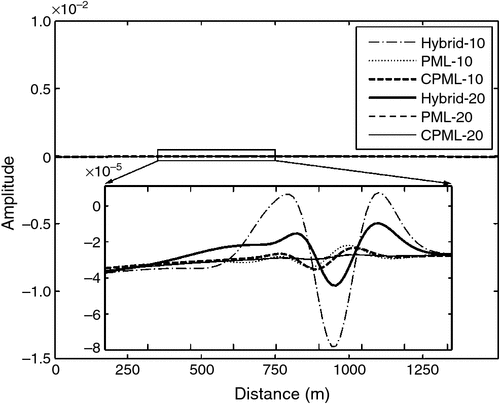
Figure 10 shows the snapshots of the wavefield at three different time steps. Figure 11 shows the differences between absorbing boundary conditions and an artificial-reflection free reference, which can be regarded as the error or artificial reflections introduced by the absorbing boundary condition. Figure 12 shows the waveforms recorded at a depth of 0 m at different time steps. The maximum value of the wavefield records is 0.1127. Obviously, the wavefront is moving away from the source position with increasing time, and the incident angle gradually increases; finally, the wavefront grazes the boundary at large distances, as shown in Figures 10 and 11. The Higdon boundary exhibits significant artificial reflections at grazing areas, as shown in Figure 11. Nevertheless, the hybrid ABC has a better absorbing performance than the Higdon boundary. However, the hybrid ABC is still less efficient for absorbing the nearly grazing incidence since it is based on a one-way wave equation.

|
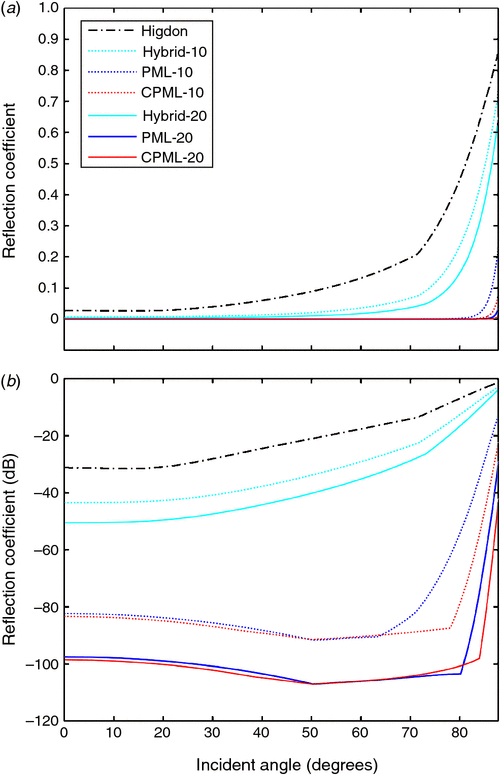
In contrast, the PML performs better than the hybrid ABC, and the CPML performs better than the PML does. The 20-layer PML performs better than the 10-layer CPML when the grazing effects are not so obvious at short traveltimes; in contrast, when the grazing effects are strong at long travel times, the CPML shows it to be necessary to absorb these grazing waves, as shown in Figures 13 and 14. Figure 15 shows the single-trace records using different boundary conditions. For the convenience of comparing the absorption performances of different boundary conditions, we calculate the numerical reflection coefficient using

where pref is the theoretical wavefield without artificial reflections, and the pmod is the wavefield with different artificial boundary conditions. Figure 16a shows the numerical reflection coefficient for different boundary conditions at different incident angles, and Figure 16b shows the decibel (dB) values of numerical reflection coefficient calculated by
|

Figure 16b shows that the 10-layer CPML has a better absorbing performance compared with the 10-layer PML for the nearly grazing incident wave from 63° to 78°. However, the 20-layer CPML only has slight advantage over the 20-layer PML from 80° to 84°. With the same number of absorbing layers, the CPML has better absorbing performance than the PML does; however, we can still use more layers for the PML instead of using a thin CPML. In addition, we see that the 10-layer PML is better than the 20-layer hybrid ABC.
Therefore, the absorption performance from good to poor in sequence is: CPML-20, PML-20, CPML-10, PML-10, Hybrid-20, Hybrid-10, and Higdon.
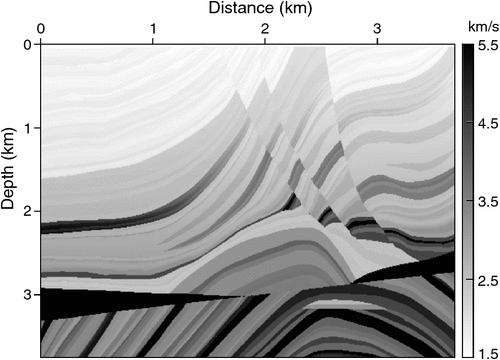
Modified Marmousi model
We test the modified Marmousi model (Figure 17), whose grid spacing is 5 m, and the grid number is 737 × 751. The upper boundary of the model is a free surface, and the other three edges are absorbing boundaries. The source is a Ricker wavelet and the dominant frequency is of 10 Hz. The source is added on the free surface and 500 m away from the left-upper corner of the model. Three kinds of boundary conditions are compared numerically: the Higdon boundary, the hybrid ABC (10 and 20 layers), the PML (10 and 20 layers), and the CPML (10 and 20 layers). There is no theoretical wavefield available as a reference for the Marmousi model; thus, we use the 50-layer CPML as a reference instead. Two groups of receivers are located along the upper and bottom boundary, respectively. The interval between two adjacent receivers is 10 m.
|
Figures 18 and 19 show the wavefield records obtained by the upper and bottom receivers, respectively. The absorption performance of the Higdon boundary is poor compared with the other methods, especially for deeper reflections. This would be harmful for the full waveform inversion. Whereas, we can see that the waveforms obtained using the Higdon boundary and hybrid ABC shown in Figure 18 are fairly close to those obtained using the PML or CPML. In fact, the artificial reflections may not be so serious to the migration results as to the full waveform inversion since the imaging result is not so sensitive to the amplitude. Thus, the Higdon boundary is still a good candidate for migration velocity analyses based on reverse time migration, due to its simplicity and very low computational cost as well as memory demand.
The absorption performance of the 20-layer CPML is the best among the three methods listed; however, its computational cost and memory demand are bigger than that of the 20-layer PML. In addition, it only shows negligible superiority over the 20-layer PML for most cases. Therefore, we can use 20-layer PML instead in most of the middle-sized models (i.e. the usual cases), except that the source is close to the left or right boundaries, which may encounter severe grazing effects.
Discussion
In the above three numerical experiments, we use θ1 = 0 and θ2 = π/6 as the angle parameters for the second-order Higdon boundary. The main consideration is that the accuracy of the approximation of a one-way wave equation is generally no more than π/3 (60°) (Claerbout, 1985; Zhang et al., 2010); thus, we should not choose large angles. In complex media, we cannot know the exact incidence angle at the boundary; thus, we only guarantee that incident angles smaller than 60° can be handled to reduce the boundary reflections. We use θ1 = 0 just as the Clayton and Engquist boundary does. Then, we select θ2 = π/6 (30°), which is between 0° and 60°. Numerical simulations show that the absorption effect of the second-order Higdon boundary is always better than that of the second-order Clayton and Engquist boundary for a wider angle range. Higher order Higdon boundary conditions have more controllable angle parameters thus are more powerful in handling wider incident angles. However, higher order Higdon boundary conditions would have limited improvement due to the phase and the amplitude errors that are associated with the expansion of one-way wave equation (Claerbout, 1985).
Among the ABC, there is another method not mentioned in the text, which is called Liao’s ABC (Liao et al., 1984; Liao, 1996). Liao’s ABC extrapolates wave equations in the time and space domain based on the Newton’s backward differential. This method is seldom reported in seismic exploration but is widely used in electromagnetic simulations to absorb the boundary reflections (e.g. Wagner and Chew, 1995; Wang and Tang, 2010; Zhang and Yu, 2012). Wang and Tang (2010) point out that Liao’s ABC is closely related to Higdon’s space–time extrapolation method and has a nice feature of simplicity and clarity, which is of particular interest for high-order boundary treatments. To avoid confusion, we classify Liao’s method into the Higdon boundary condition since the Higdon boundary condition is already well known in the community, although Liao’s method (1984) was proposed two years earlier than the Higdon boundary (1986).
Conclusions
The artificial absorbing boundary condition plays an important role in the numerical simulation of seismic wavefields. Two main kinds of methods have been proposed for this purpose: ABCs and the absorption boundary layers (i.e. the sponge boundary, the hybrid ABC, and the PML/CPML). We derive similar absorbing boundary conditions using unified forms first, and then compare their absorbing performances by theoretical analyses and numerical experiments.
The Clayton and Engquist boundary has difficulties in dealing with the corner points, which may result in strong artificial reflections. The Reynolds boundary deals with corner points with ease, but has poor absorbing performance, since its tuning parameter would degrade the absorbing performance for the low angle incident waves when trying to improve the absorbing performance for other incident angles. The Clayton and Engquist boundary is basically a special case of the Higdon boundary; whereas, the Higdon boundary does not have problems at corner points and has the best absorbing performance among these three ABCs. Therefore, we suggest using the Higdon boundary at any time if one hopes to use the absorbing boundary condition, when the computational cost and memory demand are heavy but the demand for the absorbing performance is not so serious. For example, the migration is not so sensitive to the weak amplitude distortion caused by artificial reflections. In contrast, the full wave form inversion would have problems in the presence of weak amplitude distortion caused by artefacts.
The sponge boundary still has obstacles on determining the optimal parameters before a series of numerical tests. In addition, the sponge boundary usually has to use more layers (~30–50) to guarantee the absorbing performance; however, the PML with 10 or 20 layers would show great superiority over the sponge boundary both in computational cost and memory demand. Therefore, the sponge boundary is not suggested all the time for practical applications and one can use 10- or 20-layer PML instead.
The PML/CPML is not convenient to implement for the second-order formulation of acoustic and elastic wave equations. The hybrid ABC is the only method that can have comparable performance with the PML/CPML for the second-order wave equation. The hybrid ABC is easier in implementation than the PML and CPML, and it has a much better absorbing performance than the Higdon boundary. However, the hybrid ABC is still less efficient for absorbing nearly grazing waves since it is based on a one-way wave equation.
The 10-layer PML is accurate enough when the nearly grazing wave is not serious. The 20-layer PML is suggested for most practical applications for general size models, even in the presence of strong nearly grazing waves. The main advantage of PML is that it favours natural implementation of high-order temporal discretisation if necessary, while CPML does not. To implement CPML using high-order temporal discretisation, it is necessary to introduce auxiliary variables and equations, which will introduce extra costs in both time and memory. The 20-layer CPML is only necessary when the source is located fairly close to the boundary for large-scale models, where the nearly grazing wave is severe.
Acknowledgements
We thank Dr Youshan Liu and Dr Xiao Ma for helpful discussions. We thank Professor Wei Zhang for helpful instructions on the sponge boundary. We thank the Associate Editor and two anonymous reviewers for valuable suggestions and corrections. This research was supported by the National Natural Science Foundation of China (Grant No. 41130418) and the National Major Project of China (Grant No. 2011ZX05008–006).
References
Abarbanel, S., and Gottlieb, D., 1997, A mathematical analysis of the PML method: Journal of Computational Physics, 134, 357–363| A mathematical analysis of the PML method:Crossref | GoogleScholarGoogle Scholar |
Appelö, D., and Kreiss, G., 2006, A new absorbing layer for elastic waves: Journal of Computational Physics, 215, 642–660
| A new absorbing layer for elastic waves:Crossref | GoogleScholarGoogle Scholar |
Basu, U., and Chopra, A. K., 2004, Perfectly matched layers for transient elastodynamics of unbounded domains: International Journal for Numerical Methods in Engineering, 59, 1039–1074
| Perfectly matched layers for transient elastodynamics of unbounded domains:Crossref | GoogleScholarGoogle Scholar |
Bayliss, A., and Turkel, E., 1980, Radiation boundary conditions for wave-like equations: Communications on Pure and Applied Mathematics, 33, 707–725
| Radiation boundary conditions for wave-like equations:Crossref | GoogleScholarGoogle Scholar |
Bécache, E., Givoli, D., and Hagstrom, T., 2010, High-order absorbing boundary conditions for anisotropic and convective wave equations: Journal of Computational Physics, 229, 1099–1129
| High-order absorbing boundary conditions for anisotropic and convective wave equations:Crossref | GoogleScholarGoogle Scholar |
Bérenger, J. P., 1994, A perfectly matched layer for the absorption of electromagnetic waves: Journal of Computational Physics, 114, 185–200
| A perfectly matched layer for the absorption of electromagnetic waves:Crossref | GoogleScholarGoogle Scholar |
Bermúdez, A., Hervella-Nieto, L., and Prieto, A., 2007, An optimal perfectly matched layer with unbounded absorbing function for time-harmonic acoustic scattering problems: Journal of Computational Physics, 223, 469–488
| An optimal perfectly matched layer with unbounded absorbing function for time-harmonic acoustic scattering problems:Crossref | GoogleScholarGoogle Scholar |
Bording, R. P., 2004, Finite difference modeling – nearly optimal sponge boundary conditions: 74th Annual International Meeting, SEG, Expanded Abstracts, 1921–1924.
Cerjan, C., Kosloff, D., Kosloff, R., and Reshef, M., 1985, A nonreflecting boundary condition for discrete acoustic and elastic wave equations: Geophysics, 50, 705–708
| A nonreflecting boundary condition for discrete acoustic and elastic wave equations:Crossref | GoogleScholarGoogle Scholar |
Chew, W., and Liu, Q., 1996, Perfectly matched layers for elastodynamics: a new absorbing boundary condition: Journal of Computational Acoustics, 4, 341–359
| Perfectly matched layers for elastodynamics: a new absorbing boundary condition:Crossref | GoogleScholarGoogle Scholar |
Claerbout, J., 1985, Imaging the earth’s interior: Blackwell Scientific Publications.
Clayton, R., and Engquist, B., 1977, Absorbing boundary conditions for acoustic and elastic wave equations: Bulletin of the Seismological Society of America, 67, 1529–1540
Collino, F., 1993, High order absorbing boundary conditions for wave propagation models: straight line boundary and corner cases: Second International Conference on Mathematical and Numerical Aspects of Wave Propagation, SIAM (Newark, Delaware), 161–171.
Collino, F., and Tsogka, C., 2001, Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media: Geophysics, 66, 294–307
| Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media:Crossref | GoogleScholarGoogle Scholar |
Compani-Tabrizi, B., 1986, k-t scattering formulation of the absorptive acoustic wave equation: Wraparound and edge-effect elimination: Geophysics, 51, 2185–2192
| k-t scattering formulation of the absorptive acoustic wave equation: Wraparound and edge-effect elimination:Crossref | GoogleScholarGoogle Scholar |
Diaz, J., and Joly, P., 2006, A time domain analysis of PML models in acoustics: Computer Methods in Applied Mechanics and Engineering, 195, 3820–3853
| A time domain analysis of PML models in acoustics:Crossref | GoogleScholarGoogle Scholar |
Drossaert, F. H., and Giannopoulos, A., 2007a, Complex frequency shifted convolution PML for FDTD modelling of elastic waves: Wave Motion, 44, 593–604
| Complex frequency shifted convolution PML for FDTD modelling of elastic waves:Crossref | GoogleScholarGoogle Scholar |
Drossaert, F. H., and Giannopoulos, A., 2007b, A nonsplit complex frequency-shifted PML based on recursive integration for FDTD modeling of elastic waves: Geophysics, 72, T9–T17
| A nonsplit complex frequency-shifted PML based on recursive integration for FDTD modeling of elastic waves:Crossref | GoogleScholarGoogle Scholar |
Engquist, B., and Majda, A., 1977, Absorbing boundary conditions for numerical simulation of waves: Proceedings of the National Academy of Sciences of the United States of America, 74, 1765–1766
| Absorbing boundary conditions for numerical simulation of waves:Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BC3cngslKitA%3D%3D&md5=e3ed334dd89644b021a604f5ff40c408CAS | 16592392PubMed |
Engquist, B., and Majda, A., 1979, Radiation boundary conditions for acoustic and elastic wave calculations: Communications on Pure and Applied Mathematics, 32, 313–357
| Radiation boundary conditions for acoustic and elastic wave calculations:Crossref | GoogleScholarGoogle Scholar |
Festa, G., and Nielsen, S., 2003, PML absorbing boundaries: Bulletin of the Seismological Society of America, 93, 891–903
| PML absorbing boundaries:Crossref | GoogleScholarGoogle Scholar |
Festa, G., and Vilotte, J.-P., 2005, The Newmark scheme as velocity-stress time-staggering: an efficient PML implementation for spectral element simulations of elastodynamics: Geophysical Journal International, 161, 789–812
| The Newmark scheme as velocity-stress time-staggering: an efficient PML implementation for spectral element simulations of elastodynamics:Crossref | GoogleScholarGoogle Scholar |
Festa, G., Delavaud, E., and Vilotte, J. P., 2005, Interaction between surface waves and absorbing boundaries for wave propagation in geological basins: 2D numerical simulations: Geophysical Research Letters, 32, 1–4
| Interaction between surface waves and absorbing boundaries for wave propagation in geological basins: 2D numerical simulations:Crossref | GoogleScholarGoogle Scholar |
Gedney, S. D., and Zhao, B., 2010, An auxiliary differential equation formulation for the complex-frequency shifted PML: IEEE Transactions on Antennas and Propagation, 58, 838–847
| An auxiliary differential equation formulation for the complex-frequency shifted PML:Crossref | GoogleScholarGoogle Scholar |
Givoli, D., 2004, High-order local non-reflecting boundary conditions: a review: Wave Motion, 39, 319–326
| High-order local non-reflecting boundary conditions: a review:Crossref | GoogleScholarGoogle Scholar |
Givoli, D., and Neta, B., 2003, High-order non-reflecting boundary scheme for time-dependent waves: Journal of Computational Physics, 186, 24–46
| High-order non-reflecting boundary scheme for time-dependent waves:Crossref | GoogleScholarGoogle Scholar |
Hagstrom, T., and Warburton, T., 2004, A new auxiliary variable formulation of high-order local radiation boundary conditions: corner compatibility conditions and extensions to first-order systems: Wave Motion, 39, 327–338
| A new auxiliary variable formulation of high-order local radiation boundary conditions: corner compatibility conditions and extensions to first-order systems:Crossref | GoogleScholarGoogle Scholar |
Hastings, F. D., Schneider, J. B., and Broschat, S. L., 1996, Application of the perfectly matched layer (PML) absorbing boundary condition to elastic wave propagation: The Journal of the Acoustical Society of America, 100, 3061–3069
| Application of the perfectly matched layer (PML) absorbing boundary condition to elastic wave propagation:Crossref | GoogleScholarGoogle Scholar |
Higdon, R. L., 1986, Absorbing boundary conditions for difference approximations to the multidimensional wave equation: Mathematics of Computation, 47, 437–459
Higdon, R. L., 1987, Numerical absorbing boundary conditions for the wave equation: Mathematics of Computation, 49, 65–90
| Numerical absorbing boundary conditions for the wave equation:Crossref | GoogleScholarGoogle Scholar |
Higdon, R. L., 1990, Radiation boundary conditions for elastic wave propagation: SIAM Journal on Numerical Analysis, 27, 831–869
| Radiation boundary conditions for elastic wave propagation:Crossref | GoogleScholarGoogle Scholar |
Higdon, R. L., 1991, Absorbing boundary conditions for elastic waves: Geophysics, 56, 231–241
| Absorbing boundary conditions for elastic waves:Crossref | GoogleScholarGoogle Scholar |
Hustedt, B., Operto, S., and Virieux, J., 2004, Mixed-grid and staggered-grid finite-difference methods for frequency-domain acoustic wave modelling: Geophysical Journal International, 157, 1269–1296
| Mixed-grid and staggered-grid finite-difference methods for frequency-domain acoustic wave modelling:Crossref | GoogleScholarGoogle Scholar |
Katsibas, T. K., and Antonopoulos, C. S., 2002, An efficient PML absorbing medium in FDTD simulations of acoustic scattering in lossy media: Proceedings - IEEE Ultrasonics Symposium, 1, 551–554
Komatitsch, D., and Martin, R., 2007, An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation: Geophysics, 72, SM155–SM167
| An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation:Crossref | GoogleScholarGoogle Scholar |
Komatitsch, D., and Tromp, J., 2003, A perfectly matched layer absorbing boundary condition for the second-order seismic wave equation: Geophysical Journal International, 154, 146–153
| A perfectly matched layer absorbing boundary condition for the second-order seismic wave equation:Crossref | GoogleScholarGoogle Scholar |
Kosloff, R., and Kosloff, D., 1986, Absorbing boundaries for wave propagation problems: Journal of Computational Physics, 63, 363–376
| Absorbing boundaries for wave propagation problems:Crossref | GoogleScholarGoogle Scholar |
Kristek, J., Moczo, P., and Galis, M., 2009, A brief summary of some PML formulations and discretizations for the velocity-stress equation of seismic motion: Studia Geophysica et Geodaetica, 53, 459–474
| A brief summary of some PML formulations and discretizations for the velocity-stress equation of seismic motion:Crossref | GoogleScholarGoogle Scholar |
Kuzuoglu, M., and Mittra, R., 1996, Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers: IEEE Microwave and Guided Wave Letters, 6, 447–449
| Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers:Crossref | GoogleScholarGoogle Scholar |
Lan, H., Chen, J., Zhang, Z., Liu, Y., and Zhao, J., 2013, Application of the perfectly matched layer in numerical modeling of wave propagation with an irregular free surface: 83rd Annual International Meeting, SEG, 3515–3520.
Liao, Z. P., 1996, Extrapolation non-reflecting boundary conditions: Wave Motion, 24, 117–138
Liao, Z, Huang, K, Yang, B, and Yuan, Y, 1984, A transmitting boundary for transient wave analyses: Scientia Sinica (Series A), 27, 1063–1076
Liu, Q., 1998, The pseudospectral time-domain (PSTD) algorithm for acoustic waves in absorptive media: IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 45, 1044–1055
| The pseudospectral time-domain (PSTD) algorithm for acoustic waves in absorptive media:Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BD1c%2Fos1Oisg%3D%3D&md5=e20314bec414148f9b608e902370fed2CAS |
Liu, Q., 1999, Perfectly matched layers for elastic waves in cylindrical and spherical coordinates: The Journal of the Acoustical Society of America, 105, 2075–2084
| Perfectly matched layers for elastic waves in cylindrical and spherical coordinates:Crossref | GoogleScholarGoogle Scholar |
Liu, Y., and Sen, M. K., 2010, A hybrid scheme for absorbing edge reflections in numerical modeling of wave propagation: Geophysics, 75, A1–A6
| A hybrid scheme for absorbing edge reflections in numerical modeling of wave propagation:Crossref | GoogleScholarGoogle Scholar |
Liu, Y., and Sen, M. K., 2012, A hybrid absorbing boundary condition for elastic staggered-grid modeling: Geophysical Prospecting, 60, 1114–1132
| A hybrid absorbing boundary condition for elastic staggered-grid modeling:Crossref | GoogleScholarGoogle Scholar |
Liu, Q., and Tao, J., 1997, The perfectly matched layer for acoustic waves in absorptive media: The Journal of the Acoustical Society of America, 102, 2072–2082
| The perfectly matched layer for acoustic waves in absorptive media:Crossref | GoogleScholarGoogle Scholar |
Luebbers, R. J., and Hunsberger, F., 1992, FDTD for Nth-order dispersive media: IEEE Transactions on Antennas and Propagation, 40, 1297–1301
| FDTD for Nth-order dispersive media:Crossref | GoogleScholarGoogle Scholar |
Marcinkovich, C., and Olsen, K., 2003, On the implementation of perfectly matched layers in a three-dimensional fourth-order velocity-stress finite difference scheme: Journal of Geophysical Research - Solid Earth, 108, 18-1–18-16
| On the implementation of perfectly matched layers in a three-dimensional fourth-order velocity-stress finite difference scheme:Crossref | GoogleScholarGoogle Scholar |
Martin, R., Komatitsch, D., Gedney, S. D., and Bruthiaux, E., 2010, A high-order time and space formulation of the unsplit perfectly matched layer for the seismic wave equation using Auxiliary Differential Equations (ADE-PML): Computer Modeling in Engineering & Sciences, 56, 17–41
Nataf, F., 2013, Absorbing boundary conditions and perfectly matched layers in wave propagation problems: Direct and Inverse Problems in Wave Propagation and Applications, 14, 219–231
Pasalic, D., and McGarry, R., 2010, Convolutional perfectly matched layer for isotropic and anisotropic acoustic wave equations: 80th Annual International Meeting, SEG, Expanded Abstracts, 2925–2929.
Peng, C, and Toksöz, M. N., 1995, An optimal absorbing boundary condition for elastic wave modeling: Geophysics, 60, 296–301
Qi, Q., and Geers, T. L., 1998, Evaluation of the perfectly matched layer for computational acoustics: Journal of Computational Physics, 139, 166–183
| Evaluation of the perfectly matched layer for computational acoustics:Crossref | GoogleScholarGoogle Scholar |
Rabinovich, D., Givoli, D., and Bécache, E., 2010, Comparison of high-order absorbing boundary conditions and perfectly matched layers in the frequency domain: International Journal for Numerical Methods in Biomedical Engineering, 26, 1351–1369
| Comparison of high-order absorbing boundary conditions and perfectly matched layers in the frequency domain:Crossref | GoogleScholarGoogle Scholar |
Reynolds, A. C., 1978, Boundary conditions for the numerical solution of wave propagation problems: Geophysics, 43, 1099–1110
| Boundary conditions for the numerical solution of wave propagation problems:Crossref | GoogleScholarGoogle Scholar |
Roden, J. A., and Gedney, S. D., 2000, Convolutional PML (CPML): an efficient FDTD implementation of the CFS-PML for arbitrary media: Microwave and Optical Technology Letters, 27, 334–339
| Convolutional PML (CPML): an efficient FDTD implementation of the CFS-PML for arbitrary media:Crossref | GoogleScholarGoogle Scholar |
Sochacki, J., Kubichek, R., George, J., Fletcher, W., and Smithson, S., 1987, Absorbing boundary conditions and surface waves: Geophysics, 52, 60–71
| Absorbing boundary conditions and surface waves:Crossref | GoogleScholarGoogle Scholar |
Sun, W., 2003, Finite difference modeling for elastic wave field in complex media and global optimization method research [in Chinese]: Tsinghua University.
Wagner, R. L., and Chew, W. C., 1995, An analysis of Liao’s absorbing boundary condition: Journal of Electromagnetic Waves and Applications, 9, 993–1009
Wang, T., and Tang, X., 2003, Finite-difference modeling of elastic wave propagation: a nonsplitting perfectly matched layer approach: Geophysics, 68, 1749–1755
| Finite-difference modeling of elastic wave propagation: a nonsplitting perfectly matched layer approach:Crossref | GoogleScholarGoogle Scholar |
Wang, X, and Tang, S, 2010, Analysis of multi-transmitting formula for absorbing boundary conditions: International Journal for Multiscale Computational Engineering, 8, 207–219
Xie, Z., Komatitsch, D., Martin, R., and Matzen, R., 2014, Improved forward wave propagation and adjoint-based sensitivity kernel calculations using a numerically stable finite-element PML: Geophysical Journal International, 198, 1714–1747
| Improved forward wave propagation and adjoint-based sensitivity kernel calculations using a numerically stable finite-element PML:Crossref | GoogleScholarGoogle Scholar |
Xu, Y., and Zhang, J., 2008, An irregular-grid perfectly matched layer absorbing boundary for seismic wave modeling: Chinese Journal of Geophysics, 51, 1520–1526
Yang, D., Song, G., and Lu, M., 2007, Optimally accurate nearly analytic discrete scheme for wave-field simulation in 3D anisotropic media: Bulletin of the Seismological Society of America, 97, 1557–1569
| Optimally accurate nearly analytic discrete scheme for wave-field simulation in 3D anisotropic media:Crossref | GoogleScholarGoogle Scholar |
Zhang, W., and Shen, Y., 2010, Unsplit complex frequency-shifted PML implementation using auxiliary differential equations for seismic wave modeling: Geophysics, 75, T141–T154
| Unsplit complex frequency-shifted PML implementation using auxiliary differential equations for seismic wave modeling:Crossref | GoogleScholarGoogle Scholar |
Zhang, L, and Yu, T, 2012, A method of improving the stability of Liao’s higher-order absorbing boundary condition: Progress in Electromagnetics Research, 27, 167–178
Zhang, J., Wang, W., Wang, S., and Yao, Z., 2010, Optimized Chebyshev Fourier migration: a wide-angle dual-domain method for media with strong velocity contrasts: Geophysics, 75, S23–S34
| Optimized Chebyshev Fourier migration: a wide-angle dual-domain method for media with strong velocity contrasts:Crossref | GoogleScholarGoogle Scholar |
Zhou, B., 1988, On: “k-t scattering formulation of the absorptive acoustic wave equation: Wraparound and edge-effect elimination” by B. Compani-Tabrizi (Geophysics, 51, 2185–2192, December 1986): Geophysics, 53, 564–565
| On: “k-t scattering formulation of the absorptive acoustic wave equation: Wraparound and edge-effect elimination” by B. Compani-Tabrizi (Geophysics, 51, 2185–2192, December 1986):Crossref | GoogleScholarGoogle Scholar |