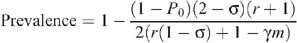Minimal impact of circumcision on HIV acquisition in men who have sex with men
Gregory J. Londish A , David J. Templeton B C , David G. Regan B , John M. Kaldor B and John M. Murray A B DA School of Mathematics and Statistics, University of New South Wales, Sydney, NSW 2052, Australia.
B National Centre in HIV Epidemiology and Clinical Research, University of New South Wales, Sydney, NSW 2052, Australia.
C Royal Prince Alfred Sexual Health, Royal Prince Alfred Hospital, Sydney, NSW 2050, Australia.
D Corresponding author. Email: J.Murray@unsw.edu.au
Sexual Health 7(4) 463-470 https://doi.org/10.1071/SH09080
Submitted: 11 August 2009 Accepted: 20 April 2010 Published: 10 November 2010
Abstract
Background: Men who have sex with men (MSM) are disproportionately affected by HIV. The proven efficacy of circumcision in reducing the risk of HIV acquisition among African heterosexual males has raised the question of whether this protective effect may extend to MSM populations. We examined the potential impact of circumcision on an HIV epidemic within a population of MSM. Methods: A mathematical model was developed to simulate HIV transmission in an MSM population. The model incorporated both circumcision and seropositioning, and was used to predict the reduction in HIV prevalence and incidence as a result of the two interventions. Estimates for the time required to achieve these gains were also calculated. Results: We derive simple formulae for the decrease in HIV prevalence with increased circumcision. Our model predicts that if an initially uncircumcised MSM population in a developed country with a baseline HIV prevalence of 10% underwent universal circumcision, HIV incidence would only be reduced to 95% of pre-intervention levels and HIV prevalence to 9.6% after 20 years. In the longer term, our model predicts that prevalence would only decrease from 10% to 6%, but this would take several generations to achieve. The effectiveness of circumcision increases marginally with higher degrees of seropositioning. Conclusions: The results of these calculations suggest that circumcision as a public health intervention will not produce a substantial decrease in HIV prevalence or incidence among MSM in the near future, and only modest reductions are achievable in the long-term.
Additional keywords: mathematical model, MSM, seropositioning.
[1]
[2]
[3] Fisher M, Pao D, Murphy G, Dean G, McElborough D, Homer G, et al. Serological testing algorithm shows rising HIV incidence in a UK cohort of men who have sex with men: 10 years application. AIDS 2007; 21 2309–14.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[4] Katz MH, Schwarcz SK, Kellogg TA, Klausner JD, Dilley JW, Gibson S, et al. Impact of highly active antiretroviral treatment on HIV seroincidence among men who have sex with men: San Francisco. Am J Public Health 2002; 92 388–94.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[5] Marcus U, Voss L, Kollan C, Hamouda O. HIV incidence increasing in MSM in Germany: factors influencing infection dynamics. Euro Surveill 2006; 11 157–60.
| CAS | PubMed |

[6] van de Wijgert JH, Shattock RJ. Vaginal microbicides: moving ahead after an unexpected setback. AIDS 2007; 21 2369–76.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[7] Yang OO. Aiming for successful vaccine-induced HIV-1-specific cytotoxic T lymphocytes. AIDS 2008; 22 325–31.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[8] Bailey RC, Moses S, Parker CB, Agot K, Maclean I, Krieger JN, et al. Male circumcision for HIV prevention in young men in Kisumu, Kenya: a randomised controlled trial. Lancet 2007; 369 643–56.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[9] Weiss HA, Halperin D, Bailey RC, Hayes RJ, Schmid G, Hankins CA. Male circumcision for HIV prevention: from evidence to action? AIDS 2008; 22 567–74.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[10] Gray RH, Kigozi G, Serwadda D, Makumbi F, Watya S, Nalugoda F, et al. Male circumcision for HIV prevention in men in Rakai, Uganda: a randomised trial. Lancet 2007; 369 657–66.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[11] Auvert B, Taljaard D, Lagarde E, Sobngwi-Tambekou J, Sitta R, Puren A. Randomized, controlled intervention trial of male circumcision for reduction of HIV infection risk: the ANRS 1265 Trial. PLoS Med 2005; 2 e298.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[12] Vittinghoff E, Douglas J, Judson F, McKirnan D, MacQueen K, Buchbinder SP. Per-contact risk of human immunodeficiency virus transmission between male sexual partners. Am J Epidemiol 1999; 150 306–11.
| CAS | PubMed |

[13] Templeton DJ, Mao L, Prestage G, Kaldor JM, Kippax S, Grulich AE. Demographic predictors of circumcision status in a community-based sample of homosexual men in Sydney, Australia. Sex Health 2006; 3 191–3.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[14] Mor Z, Kent CK, Kohn RP, Klausner JD. Declining rates in male circumcision amidst increasing evidence of its public health benefit. PLoS One 2007; 2 e861.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[15] Jin F, Prestage GP, Ellard J, Kippax SC, Kaldor JM, Grulich AE. How homosexual men believe they became infected with HIV: the role of risk-reduction behaviors. J Acquir Immune Defic Syndr 2007; 46 245–7.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[16] MacDonald A, Humphreys J, Jaffe HW. Prevention of HIV transmission in the UK: what is the role of male circumcision? Sex Transm Infect 2008; 84 158–60.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[17] Rice BD, Delpech VC, Evans BG. Could male circumcision reduce HIV incidence in the UK? HIV Med 2008; 9 329–31.
| Crossref | GoogleScholarGoogle Scholar | CAS | PubMed |

[18] Prestage G, Jin F, Zablotska I, Imrie J, Kaldor JM, Grulich AE. Trends in HIV prevalence among homosexual and bisexual men in eastern Australian states. Sex Health 2008; 5 103–7.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[19] Baral S, Sifakis F, Cleghorn F, Beyrer C. Elevated risk for HIV infection among men who have sex with men in low- and middle-income countries 2000–2006: a systematic review. PLoS Med 2007; 4 e339.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[20] Prestage G, Ferris J, Grierson J, Thorpe R, Zablotska I, Imrie J, et al. Homosexual men in Australia: population, distribution and HIV prevalence. Sex Health 2008; 5 97–102.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[21] Lohse N, Hansen AB, Pedersen G, Kronborg G, Gerstoft J, Sorensen HT, et al. Survival of persons with and without HIV infection in Denmark, 1995–2005. Ann Intern Med 2007; 146 87–95.
| PubMed |

[22] Londish GJ, Murray JM. Significant reduction in HIV prevalence according to male circumcision intervention in sub-Saharan Africa. Int J Epidemiol 2008; 37 1246–53.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[23] Millett GA, Ding H, Lauby J, Flores S, Stueve A, Bingham T, et al. Circumcision status and HIV infection among Black and Latino men who have sex with men in 3 US cities. J Acquir Immune Defic Syndr 2007; 46 643–50.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[24]
[25]
[26] Kral AH, Lorvick J, Ciccarone D, Wenger L, Gee L, Martinez A, et al. HIV prevalence and risk behaviors among men who have sex with men and inject drugs in San Francisco. J Urban Health 2005; 82(Suppl 1): i43–50.
| Crossref | GoogleScholarGoogle Scholar | PubMed |

[27] Trichopoulos D, Sparos L, Petridou E. Homosexual role separation and spread of AIDS. Lancet 1988; 332 965–6.
| Crossref | GoogleScholarGoogle Scholar |

[28]
Appendix

|

|
Derivation of equations
The mathematical model for the number of uninfected X and infected Y MSM is described by the following system of differential equations:
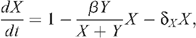
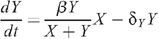
where β = 1 – (1 – p R ) n R (1 – p I (1 – γm)) n I with the following parameters:

|
Population sizes are scaled so that the rate of entry of new MSM to the uninfected population is 1 per year. The infection term (β Y/(X + Y))X is the harmonic mean of the uninfected and infected populations scaled by an infection transmission parameter β. The harmonic mean has the useful property of reducing to the smaller population if there is a large discrepancy between these populations, since the number of infections should depend more on the number of infected men, who are the minority in the population. Also the harmonic mean increases linearly as the populations increase and so the number of partnerships per man increases linearly as more men enter the population. Since the probability of HIV transmission per UAI act is small,12 β simplifies to
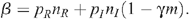
From these equations, the stable equilibrium solution can be found:
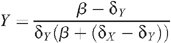
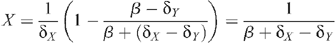
with the HIV prevalence Y/(X + Y) given by:
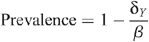
when β > δ Y . For this parameter region, the uninfected state with Y = 0 is unstable. If β ≤ δ Y then the uninfected state Y = 0 and X = 1/δ X is the only stable equilibrium (i.e. the epidemic cannot be sustained). This prevalence being non-negative indicates that the infected state is the stable solution, whereas a negative value indicates that the uninfected state is the stable equilibrium solution and prevalence reverts to zero.
Circumcision in a MSM population without seropositioning
Since p I is very much less than p R (the probability of infection for insertive UAI is small compared to the probability of being infected when receptive) and with no seropositioning (n R = n I = n), we have for a fraction m of the population being circumcised:
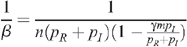
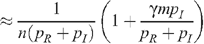
so that:
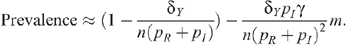
The HIV prevalence when there is no circumcision (m = 0) is given by
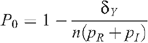
so that this last equation can be rewritten as:
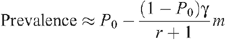
where r = p R /p I expresses the relative risk of receptive to insertive acts. This is the approximation used in estimates of the protective effect of circumcision in an MSM population.
Circumcision in a MSM population practicing seropositioning
We now consider how prevalence changes with circumcision where seropositioning is practised. With seropositioning, the number of acts between infected and uninfected individuals is assumed to remain constant, but the ratio of receptive to insertive acts between these individuals changes. We assume here that the number of UAI acts, N, is constant regardless of the level of seropositioning.
The level of seropositioning is described by the variable σ = 1 – n R /n I such that σ = 0 represents no seropositioning so that the number of receptive and insertive acts are equal between HIV-infected and uninfected individuals, and σ = 1 represents full seropositioning so that there are no receptive acts by an uninfected MSM with an infected MSM. HIV prevalence with circumcision under different levels of seropositioning is given by:
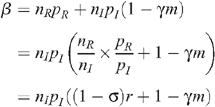
Since we assume that the total number of UAI is unchanged by seropositioning,
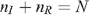
then:
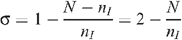
and the number of insertive UAI acts is given by n I = N/(2 – σ). Therefore:
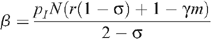
and:
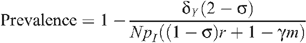
Prevalence in the absence of circumcision and seropositioning is given by
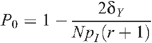
so that: