Analytical model to predict the self-induced acceleration and deceleration of a head fire

Domingos Xavier Viegas; Carlos Ribeiro; Luís M. Ribeiro; Miguel Almeida; Tiago Rodrigues; Thiago Fernandes Barbosa

doi:10.1071/WF24166

RESEARCH ARTICLE (Open Access)

Previous Next Contents Vol 34(7)

Analytical model to predict the self-induced acceleration and deceleration of a head fire

Domingos Xavier Viegas ^A ^* , Carlos Ribeiro

^A , Luís M. Ribeiro

^A , Miguel Almeida ^A , Tiago Rodrigues ^A and Thiago Fernandes Barbosa ^A

+ Author Affiliations

- Author Affiliations

^A Department of Mechanical Engineering, ADAI, University of Coimbra, Rua Luís Reis Santos, Pólo II, 3030‐788 Coimbra, Portugal.

^* Correspondence to: xavier.viegas@dem.uc.pt

International Journal of Wildland Fire 34, WF24166 https://doi.org/10.1071/WF24166

Submitted: 14 October 2024 Accepted: 22 May 2025 Published: 8 July 2025

© 2025 The Author(s) (or their employer(s)). Published by CSIRO Publishing on behalf of IAWF. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)

Abstract

Background

Current fire behaviour modelling assumes that the head fire rate of spread (ROS) depends on the three factors of the classical fire environment triangle (fuel, meteorology and topography) without considering the convective processes resulting from the interaction between fire and the environment.

Aims

An analytical model is proposed to predict the large-amplitude oscillations of the head fire ROS caused by this interaction, which often lead to rapid acceleration and deceleration of the fire.

Methods

A mathematical model proposed earlier is applied to the head fire’s acceleration and deceleration phases, using results from laboratory, field-scale and wildfires, to develop the parameters.

Key results

Two sets of model parameters were proposed to predict the temporal variation of the ROS in the laboratory and field-scale fires. Using data from wildfires, the present model predicts the time lapses of given periods of acceleration or deceleration with sufficient accuracy.

Conclusions

An analytical model is proposed to predict the large amplitude temporal variation of the head fire ROS during large fires. This model will go beyond current fire behaviour models that do not explain and predict these acceleration and deceleration processes.

Implications

The present analytical model to predict the acceleration and deceleration of the head fire proposes a novel interpretation of the fire behaviour, considering its dynamic effects and their inclusion in fire spread modelling.

Keywords: acceleration fires, canonical cases, deceleration fires, dynamic fire behaviour, eruptive fires, extreme fire behaviour, fire dynamics, fire modelling, fire spread.

Introduction

It is recognised that the interaction between a wildfire and its environment produces convective flows that modify its spread conditions in a dynamic way (cf. Santoni et al. 2000; Viegas 2004; Viegas and Pita 2004; Finney et al. 2015; Thomas et al. 2015; Filkov et al. 2020; Viegas et al. 2021, 2022). These convective processes affect the entire perimeter of the fire, modifying its propagation properties over time (cf. Viegas et al. 2024). Of particular relevance in the analysis of fire spread is the evolution of the head fire, given its contribution to the overall growth of the fire. It was found that even in nominally permanent and constant boundary conditions, the head fire varies continuously in the course of time in an oscillatory or intermittent form, with an amplitude and a frequency of oscillation that is related to the average value of the rate of spread (ROS) and to the overall properties of the fire (cf. Viegas et al. 2021, 2022). In these oscillations, it was observed that the acceleration phase of the cycle has generally a longer duration than the deceleration phase. Sometimes it is observed that after an acceleration, a very rapid deceleration is observed. While for the fire acceleration several explanations are found in the literature, rather than the convective positive feedback effect proposed by Viegas (2004, 2006), like for example the ‘flame attachment concept’, the ‘volatile organic compounds combustion’, the presence of a ‘thermal belt’, a ‘downburst’ or the ‘passage of a weather front’, the deceleration process seems to be difficult to explain in physical terms. As it was already mentioned in Viegas et al. (2022), in the literature some unlikely processes have been cited to explain the sudden reduction of ROS, which can significantly slow or even nearly halt the fire spread. Examples of these processes are the presence of fuels with different properties, namely with higher moisture content, like in the case of the Sundance Fire (Idaho Panhandle National Forests) in August 1967 (cf. Anderson 1968; Finklin 1973) in which the approach of moist air is invoked without explaining how it acts to promote a ROS reduction in a period shorter than the time lag of the fuel bed. In the case of the Air Force Bomb Range Fire (eastern North Carolina) in 1971, short distance spotting is indicated as a mechanism to promote the fire acceleration during the four pulsations that were reported for the head fire, but no justification was given for the corresponding deceleration phases (cf. Wade and Ward 1973). In their report of the Mack Lake Fire (Huron National Forest) in 1980, where the head fire accelerated to a ROS of around 9.7 km h⁻¹ in a period of 120 min and dropped dramatically to 2.2 km h⁻¹ in less than 90 min, Simard et al. (1983) propose five hypotheses, like the ones presented above, to justify the behaviour of the fire, especially its sudden deceleration.

In Rothermel (1991), the author analysed the problem of predicting the behaviour of crown fires, namely their expected size and intensity, recognising that a severe crown fire may run for several hours. It is said that as fire spreads, the intensity can rise and fall with variations in weather, topography and fuels. It is interesting to notice that only changes of the three factors of the ‘classical fire environment triangle’ (fuel, topography and weather) are invoked as the producers of the fire spread variations, without mentioning the fire-induced convection (Countryman 1972). Rothermel (1991) considered that the most prominent behaviour patterns for crown fires are the wind-driven fires and the plume-dominated fires. These concepts are currently applied to surface fires as well. It is mentioned that a fire acceleration of a wind-driven crown fire occurs on steep slopes and that the formation of fire brands is accompanied by the development of a strong convection column, without actually mentioning its effect on modifying the fire behaviour. It is observed that after running up the side of a mountain, the fire ‘often stops at the top of a ridgeline where discontinuous fuels or fuels at high moisture content may be encountered’. Once again external factors are used to justify the change of the fire behaviour, in this case a deceleration and a virtual stoppage. Then the so called ‘plume-dominated’ fires are described as being associated with relatively low wind speeds. These are also called ‘topography fires’, as the very tall convection columns that are associated to eruptive fires that occur in canyons or in complex topography. Both designations are misleading as wind and topography factors are always present in a large and fast spreading fire and with very few exceptions, we cannot separate one behaviour from the other. These patterns are phases of the same fire event spreading under permanent boundary conditions, as observed in Viegas et al. (2021, 2022). In Rothermel (1991), the author admits that fires are seldom uniform and well behaved, ‘their behaviour can be expected to change rapidly as environmental, fuel and topographic features change. During the course of a running crown fire, one or more of these behaviour patterns may be displayed’. Once again, only external factors from the classical ‘triangle’ are mentioned to explain the changes in fire behaviour patterns.

In this article, the problem of a fire acceleration followed by a sudden deceleration of the head fire is addressed. Following a previous analytical model to predict the effect of the feedback of the fire-induced convection on the modification of the ROS of the head fire that was developed for eruptive fires, the same concept and model are applied to the deceleration process. Using data from a set of laboratory scale experiments, or test cases, that were performed by the authors under well-defined conditions that are described below, which are designated as ‘canonical cases’, data from field scale experiments and from wildfires, it is shown that the acceleration and deceleration processes that are observed in a wide range of scales are well explained by the proposed model. Given the promising results obtained, the model is proposed to be employed in operational conditions. This would help estimate the amplitude and duration of fire acceleration and deceleration, aiding in the safer and more efficient management of fire suppression teams.

Methodology

Conceptual temporal evolution of the ROS

From the observations made in the analysis of the three canonical cases (Ribeiro 2024) and of a large number of fires spreading freely at different scales, under nominally permanent and uniform boundary conditions, we verify that starting with a given value R_i of the ROS at the time t_i, the spread of the fire usually consists of an acceleration phase, during which the ROS of the head fire increases gradually or with oscillations, reaching values R₁ at t₁, and R₂ at t₂, as shown schematically in Fig. 1. As was shown in Viegas (2006), in the analysis of eruptive fires in canyons, this growth is due to the feedback effect of the interaction between the fire and the surrounding atmosphere. This feedback process inducing fire acceleration was found by the authors initially in eruptive fires in canyons or on steep slopes (cf. Viegas 2004, 2006; Viegas and Pita 2004; Rodrigues et al. 2019, 2023; Xie et al. 2020), but it is present in fires of all sizes and timescales that behave dynamically, due to the interaction between the fire and its surroundings (cf. Viegas et al. 2022).

Fig. 1.

Temporal evolution of the rate of spread (shown as R) in the course of time (shown as t) during a period of acceleration and deceleration processes. Relevant values of rate of spread and their corresponding times are identified in this figure and described in the text.

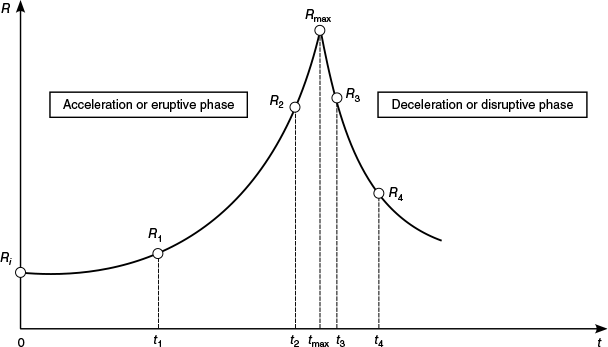
Theoretically, according to the model proposed in Viegas (2004), the ROS can reach very high values within a finite period of time or over a finite travel distance. However, physical limits constrain this growth, and the ROS cannot become infinite. It is observed in experimental and in wildfires that the value of the ROS reaches a maximum value R_max after a certain period of time, at t_max and then it starts to decrease. This fire deceleration is caused by the opposing flow induced by fire development on the leeward side of the flame (opposite to the main wind direction), moving towards the unburned fuel.

The velocity of the backflow increases, reducing the ROS of the fire front to values like R₃ at t₃ and R₄ at t₄, as illustrated in Fig. 1. and confirmed by experimental data. It is observed that the process of fire deceleration is very intense and the period of fire deceleration is generally shorter than that of acceleration (Viegas et al. 2022).

Mathematical model

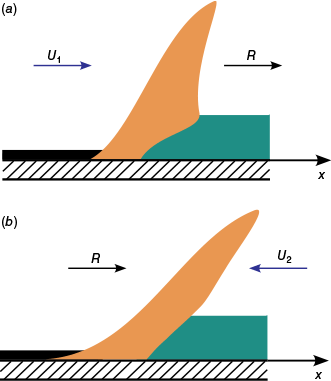
We now address the problem of determining a mathematical model to predict the acceleration and deceleration phases of the fire (Fig. 2). The starting point of this analytical semi-empirical approach is the model proposed to predict the acceleration phase of an eruptive fire by Viegas (2004).

Fig. 2.

Schematic vertical cross section geometry of a flame front of the head fire in its symmetry plane. (a) In the acceleration or eruptive phase; (b) in the deceleration phase. R Rate of Spread; U₁ Characteristic flow velocity on the windward side; U₂ reverse flow on the opposite side of the fire front, on the leeward side.

Acceleration phase

In the case of an eruptive fire in a canyon, Viegas (2004) proposed a mathematical model to predict the variation of the ROS of a head fire, due to the feedback effect between the fire induced flow on the surrounding environment, producing a growth of the fire due to the enhancement of the flaming combustion and therefore of the ROS value. A brief review of this model is provided here and in Fig. 2a, a typical stage of the fire acceleration or eruptive phase is depicted.

The following definitions are used in the formulation of the present model:

(1)

Non - dimensional or relative ROS : R' = \frac{R}{R_{o}}

In this equation R is the instantaneous value of the ROS and R_o is the basic ROS, corresponding to a linear fire front spreading in the same fuel bed in the absence of slope or wind (cf. Viegas 2004, 2006; Viegas et al. 2013, 2021, 2022; Raposo et al. 2014, 2015, 2018; Xie et al. 2014; Rodrigues et al. 2019; Ribeiro et al. 2022, 2023).

(2)

Non - dimensional wind velocity : U' = \frac{U}{U_{o}}

In this equation U is the characteristic value of the flow velocity near the fire front and U_o is the reference flow velocity; in the present work the value of U_o = 1 m s⁻¹ (for more details on this definition see Viegas 2004).

(3)

Non - dimensional time lapse : t' = \frac{t}{t_{o}}

In this equation t is the time elapsed since the start of the fire and t_o is the residence time of the fire in the fuel bed, (for more details on this definition see Viegas 2004, 2006; Wotton et al. 2012; Raposo et al. 2018). Assuming that the ROS depends on the local reference flow velocity, following a relationship such as:

(4)

R' = 1 + a_{1} U^{b_{1}}

And that the energy release that is associated to a fire front with a ROS R, induces a change of dU′ of the local velocity in an infinitesimal period of time dt, that is given by:

(5)

d U' = a_{2} {R'}^{b_{2}} d t

In the previous equations, the coefficients a₁, and a₂ and the exponents b₁ and b₂ can be empirically determined for a given fuel bed through a set of experiments. Combining the previous equations, it is possible to eliminate the explicit dependence on the local flow velocity and find that the rate of variation of the ROS with time is given by:

(6)

\frac{d R'}{d t} = {a_{1}}^{\frac{1}{b_{1}}} b_{1} a_{2} {(\frac{R' - 1}{a_{1}})}^{1 - \frac{1}{b_{1}}} {R'}^{b_{2}}

Using the following additional definitions for dimensionless parameters:

(7)

a_{1}^{'} = a_{1} {U_{o}}^{b_{1}}

(8)

a_{2}^{'} = a_{2} t_{o}

Eqn 6 can be written in the following non-dimensional form:

(9)

\frac{d R'}{d t} = a_{1}^{' \frac{1}{b_{1}}} b_{1} a_{2}^{'} {(R' - 1)}^{1 - \frac{1}{b_{1}}} {R'}^{b_{2}}

This differential equation shows that whenever R′ ≠ 1 then $d R' / d t \neq 0,$ so there will be a change of the ROS of the fire in the course of time. As we know R′ = 1 corresponds to R = R_o, meaning that only in the limiting case of a fire spreading on a horizontal surface in the absence of wind, there will be a steady-state spread of the fire front. It must be noted that in a back fire and at the flanks of a certain fires, it is observed that R ≈ R_o, so the steady state condition is approximately fulfilled in those cases as well.

As all the parameters in Eqn 9 are positive the ROS variation is positive and the fire will accelerate as in an eruptive fire. Integrating Eqn 9 from the initial conditions to the present time, we can determine the instantaneous ROS value:

(10)

R' = R_{i} + \int_{t_{i}}^{t'} \frac{d R'}{d t'} \times d t'

Integrating the function R(t) between two values of time t₁ and t₂, it is possible to estimate the distance travelled by the fire in that period of time. The calculation of this distance, during either acceleration or deceleration phases of the fire is straightforward, but in spite of its great practical importance, to keep the paper simple and short, we will not explore this capacity of the model here.

Determination of the model parameters

In Viegas (2006), the determination of the parameters of the fire acceleration model, based on laboratory experiments, is presented in detail. A brief review is provided here, as a similar process is followed in this work for the deceleration phase model.

The basic ROS R_o is determined from experiments or from the analysis of the back fire of wildfires, but it can, in principle, be determined from fire simulation models, like the Rothermel model as it corresponds to the simple case of no slope and no wind conditions, in which these models are applicable.

The residence time t_o was also determined from experiments, although there are physical models to estimate its value as a function of the physical and thermal properties of the fuel bed particles and their overall arrangement (Nelson 2003).

The parameters a₁ and b₁ were determined from laboratory experiments on fire spread in a wind tunnel, conducted for a series of fuel beds. In this case, the wind velocity was considered as that of the undisturbed flow out of the boundary layer of the flow, which is an approximation.

The evaluation of parameters a₂ and b₂, which are specific to the eruptive model, was performed from experimental data obtained in tests of eruptive fires in canyons. Manipulating the above equations, the following equation can be obtained, in which the unknown parameters a₂ and b₂ are expressed as a function of the other parameters that are already known or can be determined experimentally.

(11)

Y = \frac{d R'}{d t'} \frac{{(R' - 1)}^{\frac{1}{b_{1}} - 1}}{a_{1}^{'}^{\frac{1}{b_{1}}} b_{1}} = a_{2}^{'} {R'}^{b_{2}}

Deceleration phase

In Fig. 2b a typical stage of the fire deceleration phase is represented. It is assumed that the deceleration process is caused by the reverse flow U₂ on the opposite side of the fire front (cf. Viegas et al. 2021). Although there is a relation between the characteristic flow velocity U₁ on the windward side of the fire with the value U₂ of the flow velocity on the leeward side of the flame, we will focus this component and its effect on the variation of the ROS of the fire front.

The effect of the reverse flow is somehow similar to that of the windward flow, in terms of accelerating the fire front, but now with a negative effect. This flow has a drag effect on the fire front and as it reduces the inclination of the flame, it contributes to reducing the ROS. Besides, the negative flow velocity reduces the modulus of the effective local velocity near the combustion zone. Therefore, it reduces its intensity and consequently, the ROS. Given the feedback between the fire and its surroundings, this process is self-sustaining, leading to a consecutive reduction of the ROS and of the surrounding flow, until the boundary conditions, associated to the ambient wind or to the local topography that may trigger another acceleration cycle. It is observed that the overall effect of this process is to decelerate the fire in a very effective way, reducing the ROS much faster than during the acceleration phase, as found in the case studies.

We postulate that the deceleration process is governed by a similar law, but with different parameters. Let us assume that the R(U) is given by a similar function possibly with different parameters, but dU must now be negative and given by:

(12)

d U = - a_{3}^{⁎} R^{b_{3}} d t

(13)

d U' = - a_{3} {R'}^{b_{3}} d t'

(14)

\frac{d R'}{d t'} = - a_{1}^{' \frac{1}{b_{1}}} b_{1} a_{1}^{'} {(R' - 1)}^{1 - \frac{1}{b_{1}}} {R'}^{b_{3}}

If we separate the known terms from the unknown (as was done in Viegas 2006) we obtain:

(15)

Z = \frac{d R'}{d t'} \frac{{(R' - 1)}^{\frac{1}{b_{1}} - 1}}{a_{1}^{' \frac{1}{b_{1}}} b_{1}} = a_{3}^{'} {R'}^{b_{3}}

Therefore, the deceleration phase will be described by:

(16)

\frac{d R'}{d t'} = - a_{1}^{' \frac{1}{b_{1}}} b_{1} a_{3}^{'} {(R' - 1)}^{1 - \frac{1}{b_{1}}} {R'}^{b_{3}}

Displacement of the time of origin

In the application of the model an initial value of the ROS R′_i must be specified for time $t_{s}^{'} = 0 s$ to integrate Eqn 9. When it is intended to fit a set of values $(t_{s}^{' ⁎}, R_{1}^{'}) and (t_{2}^{' ⁎}, R_{2}^{'})$ to the model, it is necessary to adjust the time scale displacing its origin. The values of $t_{i}^{' ⁎}$ are measured in the physical scale of a given experiment or of a real case. Usually there are more than two data points to fit the model in each case, as it will be shown. For convenience, the time of the first point is considered to be the origin of time for that set of experimental points: $t_{1}^{' ⁎} = 0$ . Therefore, as indicated in Fig. 1, it is necessary to determine the value of time t₁ in the model that corresponds to a given value of R₁ and then define the modified time scale t* and t′* by:

(17)

t^{⁎} = t - t_{i}

(18)

t^{' ⁎} = \frac{t - t_{i}}{t_{o}}

This approach is illustrated in Fig. 3a for the acceleration or eruptive phase.

Fig. 3.

Displacement of time origin for: (a) the acceleration phase (b) deceleration phase. t^* modified time scale

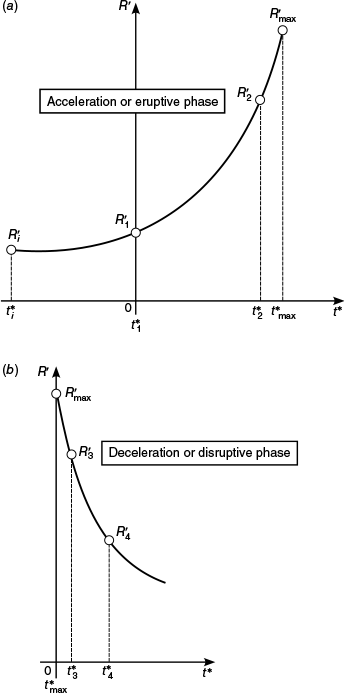
For the deceleration phase the modified time scale can be defined by:

(19)

t^{⁎} = t_{\max} - t_{i}

Or in non-dimensional form:

(20)

t^{' ⁎} = \frac{t_{\max} - t}{t_{o}}

This approach is illustrated in Fig. 3b for the deceleration phase.

Canonical cases

Definition

In order to systematically study wildfire spread under controlled conditions that can be replicated by different researchers, we defined a set of test cases that are performed in the carefully controlled conditions of a laboratory. In these cases, the fire spread properties can be characterised and measured with the required detail and accuracy. We propose these as “canonical cases” in the sense that they can be considered as benchmark situations that can be replicated and analysed by different researchers anywhere in the World, analytically, numerically or experimentally. The experimental simulation can be made in a laboratory or at a field scale, as we did for all of them. These situations can also be observed and documented in wildfires, although certainly with much less control of the parameters and measurement accuracy.

The canonical cases considered in this study are:

Point ignition fire in a slope
Point ignition fire in a canyon
Intersection of two fire lines or junction fire.

The experimental results used in this study were all obtained at the Forest Fire Research Laboratory (LEIF) of the University of Coimbra, using test rigs that were described in previous publications (Viegas and Pita 2004; Viegas et al. 2013, 2021, 2022; Xie et al. 2014; Raposo et al. 2018; Ribeiro et al. 2023; Ribeiro 2024). In most experiments, the fuel bed was composed by a uniform layer of dead needles of Pinus pinaster with a load of 0.6 kg m⁻² (dry mass) with a moisture content depending on the ambient laboratory conditions. In each experiment, the basic ROS R_o was measured in a horizontal fuel bed with 1 × 1 m² and the corresponding value is given in Table 1.

Table 1.Parameters of laboratory scale experiments used in the present study.

Case	Ref.	α (°)	m_f (%)	R_o (cm s⁻¹)	R₁ (cm s⁻¹)	$t_{1}^{⁎}$ (s)	R₂ (cm s⁻¹)	$t_{2}^{⁎}$ (s)	R₃ (cm s⁻¹)	$t_{3}^{⁎}$ (s)	R₄ (cm s⁻¹)	$t_{4}^{⁎}$ (s)
Slope	SP201	20	12.5	0.31	0.56	25	0.72	550	–	–	–	–
	SP301	30	12.5	0.31	0.51	310	1.07	550	1.16	810	1.06	970
	SP401	40	12.5	0.31	0.312	460	1.73	680	–	–	–	–
Canyon	DE304	20	10.3	0.28	0.38	502.5	2.82	582.5	1.8	772.5	1.5	812.5
	DE310	30	10.3	0.28	0.52	562.5	9.87	637.5	6.3	702.5	3.7	712.5
	DE309	40	9.0	0.22	0.74	592.5	10.9	647.5	9.1	702.5	7.4	705
Junction	JF0030	0	10.9	0.35	–	–	–	–	3.1	735	0.5	965
	JF1030	10	13.8	0.23	4.82	624	7.03	656	2.2	754	0.6	906
	JF2030	20	13.9	0.23	–	–	–	–	19.3	692	1.9	744
	JF3030	30	13.6	0.21	18.6	655.5	41.7	673.5	30.4	683	24.9	687
	JF3040	40	11.8	0.26	14.8	670.5	53.1	682.5	22.9	683	18.6	687

Experiments with other fuel beds (straw and shrubs) were performed as well, which presented similar results that are not reported here.

Point ignition fire in a slope

The tests used in this case were described in Viegas et al. 2021. The size of the fuel bed was 2 × 5.5 m² (in some tests, the dimensions were 2 × 5 m²) and the slope of the table varied between 0° and 40°. The ignition point was placed in the axis of the fuel bed 50 cm above its bottom. The evolution of the fire was registered using a pair of video and infrared (IR) cameras placed above the table. The (IR) images were analysed in order to determine the perimeter of the fire at each time step and the ROS of the head fire. It is estimated that the absolute error of the ROS in these experiments was lower than 0.1 cm s⁻¹.

The parameters of the tests of the point ignition fires are given in Table 1.

Point ignition fire in a canyon

The canyon experiments used were performed in the Canyon Table, with 3 × 3 m² using the methodology described in Viegas and Pita (2004) and Viegas et al. (2021). The correspondent parameters are given in Table 1.

Intersection of two fire lines or junction fires

The rate of advance of the intersection point of two fire lines making an angle of 30° between them was measured according to the methodology described in Raposo et al. (2018) and Ribeiro et al. (2023). In these experiments that are also designated as ‘junction fires’, the fuel bed length was 5.5 m and the slope varied between 0 and 40°. The correspondent parameters are given in Table 1 as well.

Experimental field tests

Association for the Development of Industrial Aerodynamics (ADAI) Research Team regularly performs experimental fires in plots of natural vegetation, namely shrublands composed mainly by Ericaceae and Chamaesparteum Tridentatum, in the Mountain of Lousã (cf. Viegas et al. 2002). These plots are usually of rectangular shape in varying slopes that are limited by fire breaks to ensure overall safety. Among the large amount of available experimental results, the ROS data of five plots 807, 808, 809, CF57 and CF79 burned in 2006 and 2012 with a linear ignition at the lower part of the plot will be used. The advance of the fire front was measured continuously using video and IR cameras on board of a helicopter and in fixed positions on the ground. The relevant parameters of these tests are given in Table 2.

Table 2.Parameters of field scale experimental fires that were used in the present study.

Case	Plot	Date	α (º)	R_o (cm s⁻¹)	R₁ (cm s⁻¹)	$t_{1}^{⁎}$ (min)	R₂ (cm s⁻¹)	$t_{2}^{⁎}$ (min)	R_a (cm s⁻¹)	$t_{3}^{⁎}$ (min)	R₄ (cm s⁻¹)	$t_{4}^{⁎}$ (min)
Field	807	2006	30	0.91	3.8	330	27.8	362	–	–	–	–
	809				3.8	9.1	7.3	49.6	–	–	–	–
	808				–	–	–	–	22.9		2.2
	CF57	2012		1.7	7.2	417	29.4	420	–	–	–	–
	CF79	2012		1.7	15.6	450	55.9	453	–	–	–	–

Wildfires

In 2017, a series of very large fires occurred in Central Portugal, with dramatic impacts, including a total of 119 fatalities (Haynes et al. 2020). The research team of ADAI was contracted by the Portuguese Government to analyse in detail the main fires that occurred, their behaviour and the accidents associated to them. There were two major events, the first one occurred on the 17th of June 2017, known as the Pedrógão Grande (PG) Fire that resulted in the death of 66 persons. The authors published an official report (in Portuguese) requested by the Portuguese Government, Viegas et al. (2017), and two papers Pinto et al. (2022) and Viegas et al. (2023), in which the physical processes associated with this fire and its spread were analysed. In Viegas et al. (2023) a laboratory scale simulation of the PG fire was performed to successfully illustrate the acceleration and deceleration process of the head fire. The parameters of the real fire and its laboratory scale simulations are given in Table 3.

Table 3.Parameters of the wildfires that were used in the present study.

Real fire	R_o (cm s⁻¹)	$R_{1}^{'}$ (cm s⁻¹)	$t_{1}^{⁎}$ (min)	$R_{2}^{'}$ (cm s⁻¹)	$t_{2}^{⁎}$ (min)	$R_{3}^{'}$ (cm s⁻¹)	$t_{3}^{⁎}$ (min)	$R_{4}^{'}$ (cm s⁻¹)	$t_{4}^{⁎}$ (min)
Vouzela	5.4	5.4	271	32.8	456	31.2	689	10.4	951
Oliveira do Hospital	5.9	4.3	46	23.5	392	–	–	–	–
Leiria	4.7	3.2	346	42.3	466	39.1	583	16.1	1003
Lousã	5.7	6.2	47	39.7	409	28.7	583	9.6	763
Pedrógão Grande	5.4	35.9	398	284	458	–	–	–	–
Porto de Mós	3.0	5.1	390	104.4	870
Monchique	1.5	3.1	30	57.2	90	15.6	390	34.9	450
Odemira	2.5	6.2	90	18.1	270	18.1	270	10.9	390
Castro Marim	1.1	15.8	120	107.8	990	–	–	–	–
Idanha-a-Nova	2.7	–	–	–	–	29.3	120	3.7	240
Sernancelhe	1.5	–	–	–	–	40.4	330	9.8	1770
Proença-a-Nova	1.5	–	–	–	–	48.9	150	26.8	480
Cramer Fire	6.7	7.0	408	41.3	431	–	–	–	–
Rattlesnake	7.5	2.2	373	6.3	383	–	–	–	–

The second event occurred on the 15 October 2017 and consisted of a series of nine major fires potentiated by Ophelia hurricane (Portugal) that produced very strong winds, causing major impacts, including 240 kHa burned in a single day and the death of 53 persons. The authors also produced an official report for the Portuguese Government, Viegas et al. (2019). Despite the scale and complexity of these fires, this report produced a detailed survey of each fire based on various data collection methods, including extensive field work and personnel interviews. The results obtained for the head and flank fire for several sections of each fire were analysed and used in the present work. The main parameters of each fire are given in Table 3.

On 9 July 1953, in Powder House Canyon in the Mendocino National Forest in northern California (USA), a wildfire started and was designated by Rattlesnake Fire. Before it was under control on 11 July 1953, the wildfire killed one Forest Service employee and 14 volunteer firefighters from the New Tribes Mission, as reported in Cliff et al. (1953). The total burned area was more than 1300 acres (530 ha).

The Cramer Fire incident occurred in the United States of America in 2003 and was reported by Donoghue et al. (2003). In this report, there are several graphs that show the estimated growth of the fire front over pertinent periods of the fire history. These graphs were used to calculate the rate of spread values.

Results and discussion

Model parameters

The purpose of the present paper is to verify whether the proposed model for fire acceleration and deceleration described, respectively, by Eqns 9 and 16 could provide a good representation of the time evolution of the ROS in each phase. Given the variety of cases and scales analysed, it cannot be expected that a single set of parameters should describe all situations. Despite their overall similarity, the acceleration and deceleration mechanisms differ in some details, for example if a fire occurs in a canyon or in a junction fire. It was found that it was necessary to treat laboratory-scale experiments separately and the larger scale results, like those derived from field experiments and wildfires. Therefore, the derivation of the model parameters will be presented separately for both cases.

Laboratory scale experiments

By analysing data from laboratory-scale experiments with Pinus pinaster dead needles, it was possible to determine the model parameters to obtain a good overall adjustment for the acceleration and deceleration phases, for all data points registered.

Following previous analysis, using pine needles fuel beds, the residence time t_o = 80 s, an overall adjustment was obtained with the following set of values: a₁ = 1.5 and b₁ = 2.65; $a_{2}^{'} = 0.005$ and b₂ = 2.7. These values are close, but still slightly different from those reported in Viegas (2004) obtained for fire spread in canyons: a₁ = 1.10 and b₁ = 2.02; $a_{2}^{'} = 0.0062$ and b₂ = 1.16.

Using the methodology described above (Eqns 11 and 15) for the deceleration phase, the following set of values were obtained: a₁ = 12 and b₁ = 1.0; a₃ = 0.3 and b₃ = 1.1. Using data from test JF2030-1 (Ribeiro et al. 2023) of two intersecting fire lines in pine needles, the following values were obtained: a₁ = 1.10 and b₁ = 2.02; a₃ = 0.85 and b₃ = 0.78. Once again, it should be noted that the first set of values correspond to an overall adjustment of the various experimental cases, while the second set was obtained just for the case of a junction fire, which is characterised by a peculiarly strong convective process that is not found in the other cases.

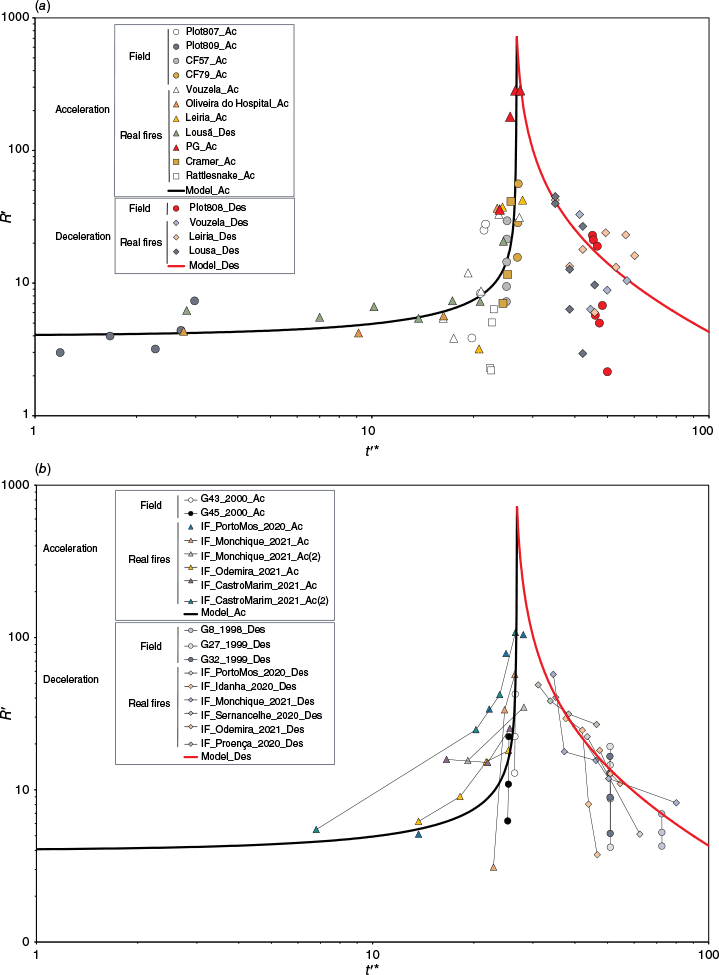
The evolution of the non-dimensional ROS R′ over time t′ as plotted in Fig. 4, was calculated by integrating Eqn 9 from the initial time t = 0 s $R_{i}^{'} = 2$ , also using the model parameters presented above. The same was done for the deceleration curve, also shown in Fig. 3, integrating Eqn 16 considering that for t =t_max the value of R′ = 312.6, which is close to the highest values obtained by the authors in previous work.

Fig. 4.

Results of the acceleration and deceleration processes for the laboratory experiments. The model curves were calculated using the parameters defined before. The identification of each data set is shown in the figure legend.

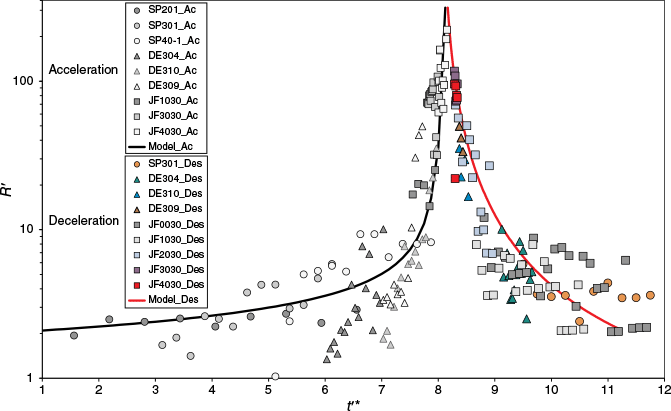
The results of the present analysis for the laboratory scale are shown in Fig. 4 in which the data points are plotted together with the model curves calculated as was described before.

Field scale experiments and wildfires

A similar procedure was followed for the results from the field experiments and wildfires. As the value of R_o could not be measured in these cases, it was determined by observing the evolution of rear or backing fires, taking care to exclude effects of wind or slope that could affect its evaluation.

The residence time t_o for the field scale fires must vary in a range of values depending on the fuel bed properties and the combustion conditions of the fire. As the purpose of the present work is to illustrate the overall applicability of the model, a reference value for field experiments and wildfires t_o = 286 and 1000 s, respectively, was adopted following Viegas (2004) or Raposo et al. (2018), to all the cases, although more specific values could be adopted for each set of fuels. More extensive research is required to determine the residence time of various fuels in different burning conditions.

For the acceleration phase the following parameters were used: a₁ = 2.5 and b₁ = 1.9; $a_{2}^{'} = 0.0003$ and b₂ = 2.7. The corresponding values for the deceleration phase were: a₁ = 0.95 and b₁ = 0.5; a₁ = 0.95, a₃ = 0.2 and b₃ = 0.9.

To determine the evolution R′(t) the initial value for the acceleration phase was $R_{i}^{'} = 4$ . For the deceleration phase the initial value, for t = t_max was $R_{\max}^{'} = 500$ as for real or field experiments higher values of $R_{\max}^{'}$ were estimated. The corresponding curves and data points from the field scale experiments and wildfires are plotted in Fig. 5a. To validate the model, additional data not used in the estimation of model parameter was analysed. These came from several fires, including information on the spread of fire isochrones calculated by the national emergency and civil protection authority and field experiments carried out by CEIF-ADAI in the past. The data points from the field scale experiments and wildfires are plotted in Fig. 5b.

Fig. 5.

(a) Results of the acceleration and deceleration processes for the field experiments and wildfires. The model curves were calculated using the parameters defined above. The identification of each data set is given in the legend. (b) Application of the acceleration and deceleration model to other field tests and wildfires.

Time delays for acceleration and deceleration in wildfires

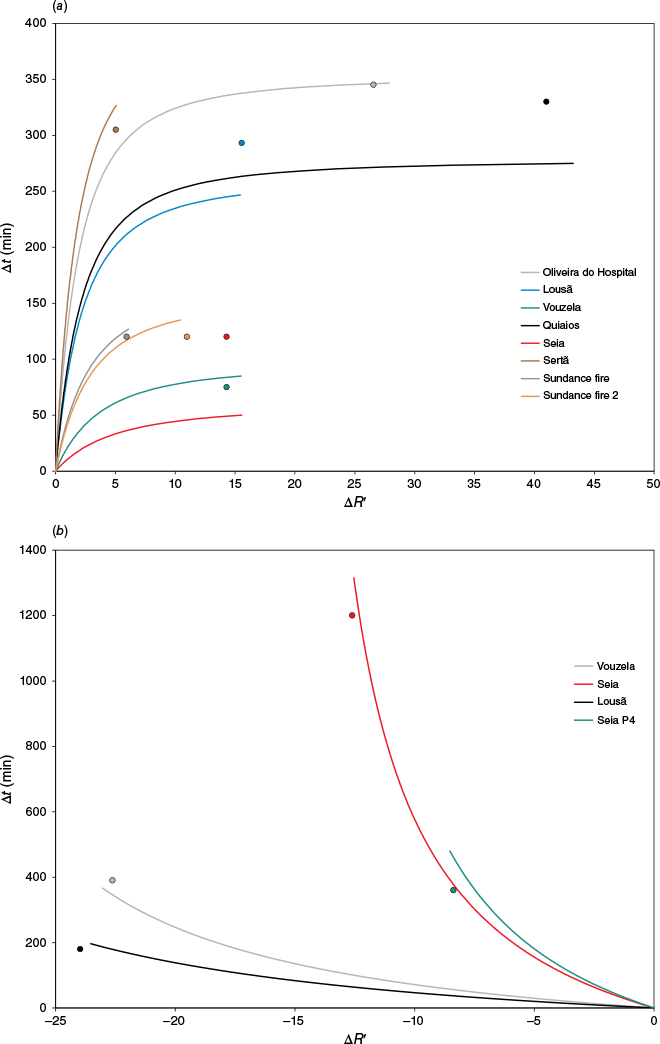
Given the relevance of applying the present model to wildfires, we now estimate the time delay required to change the ROS from its initial value to the maximum value achieved in the acceleration process, or the opposite in the deceleration phase, and compare it with the model predictions. For this we selected a series of sequences of acceleration and deceleration phases in some wildfires and estimated the corresponding values of:

For acceleration: $Δ R_{a}^{'} = R_{2}^{'} - R_{a}^{'} and Δ t_{a} = t_{2} - t_{1}$
For deceleration: $Δ R_{d}^{'} = R_{4}^{'} - R_{3}^{'} and Δ t_{d} = t_{4} - t_{3}$ .

As can be seen in Fig. 1, where the function R′(t) predicted by the analytical model, using defined values of the initial conditions $(R_{i}^{'} and R_{\max}^{'})$ is shown, for a given pair of values of $(R_{1}^{'} and R_{\max}^{'})$ it is possible to estimate the corresponding value of the time lapse Δt_a for the acceleration phase and the same for the deceleration phase. It is easy to see that: $Δ t_{a} = f (Δ R_{a}^{'}, R_{1}^{'})$ and $Δ t_{d} = f (Δ R_{d}^{'}, R_{3}^{'}) .$

This means that the time lapse Δt_a, required to have a given change of the ROS $Δ R_{a}^{'}$ , depends on $R_{1}^{'}$ , the initial value of the ROS, for the acceleration, being larger for smaller values of $R_{1}^{'}$ . Similarly, for the deceleration phase, for a fixed $Δ R_{d}^{'}$ , the time lapse Δt_d increases with decreasing values of $R_{3}^{'}$ .

In Fig. 6a, b respectively we plotted the results of time delays as a function of the respective variation of the ROS in a series of wildfires from our database, for the deceleration and for the acceleration phases. In these figures, the curves of calculated ∆t, according to the analytical model for each case, are plotted as well.

Fig. 6.

(a) Measurements of time lapse in wildfires as a function of the variation of the rate of spread and of initial values of the acceleration phase and the corresponding prediction, according to the analytical model. (b) The same for deceleration phase of some wildfires.

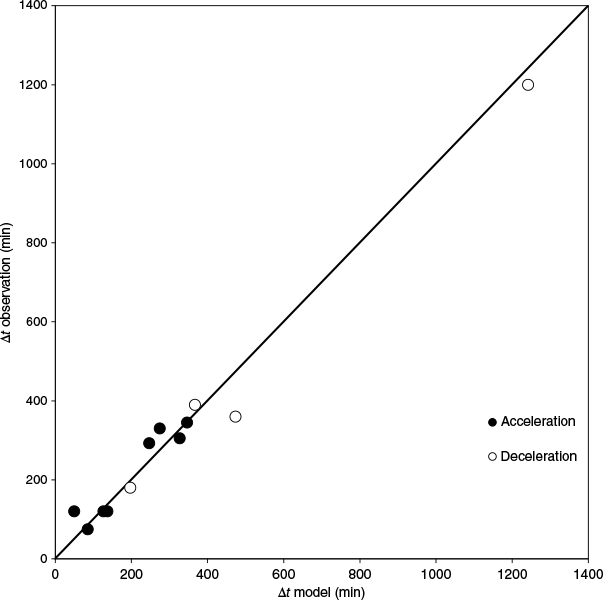
In Fig. 7, the measured values and the model predictions are compared, showing strong agreement between the two sets of values for both the acceleration and deceleration phases. Thus, the present analytical model is validated to predict time lapses for given ROS variations in wildfires. The absolute and relative error values were calculated and can be seen in Table 4.

Fig. 7.

Comparison between measured values of time lapses and predictions using the present analytical model.

Table 4.The absolute and relative error between measured values of time lapses and predictions using the present analytical model.

Real fire	Acceleration				Deceleration
	Real	Model	A. error	R. error	Real	Model	A. error	R. error
	Δt_r (min)	Δt_m (min)	Δt (min)	(%)	Δt_r (min)	Δt_m (min)	Δt (min)	(%)
Vouzela	75	85	10	13.3	390	366.7	23.3	6.0
Oliveira do Hospital	345	346	1.1	0.3%	–	–	–	–
Quiaios	330	74.6	55.4	16.8	–	–	–	–
Lousã	293	246.7	46.3	15.8	180	96.7	16.7	9.3
Seia	120	50.00	70.0	58.3	200	1241.7	41.7	3.5
Seia P4	–	–	–	–	360	473.3	113.3	31.5
Sertã	305	326.6	21.7	7.1	–	–	–	–
Sundance ac_1	120	126.7	6.7	5.6	–	–	–	–
Sundance ac_2	120	36.7	16.7	13.9	–	–	–	–

Discussion

Selection of parameters

Table 5 lists the model parameters used in the present work for the various types of tests.

Table 5.Model parameters for acceleration and deceleration phases to different types of scale laboratory test, field and wildfires.

Case	Fuel	t_o (s)	Acceleration				Deceleration
Case	Fuel	t_o (s)	a₁	b₁	$a_{2}^{'}$	b₂	a₁	b₁	a₃	b₃
Laboratory	Pine needles	80	1.5	2.65	0.005	2.7	1.2	1	0.3	1.1
Field and wildfires	Shrubs	1000	2.5	1.85	0.0003	2.73	1.1	2.02	0.002	1.4

One of the objectives of the present work was to propose the application of the acceleration and deceleration model to explain and describe the acceleration and deceleration phases of the head fire ROS under a wide range of conditions, including different scales. It was found that although the proposed models and their basic equations provide a reasonable description of the processes, it was not possible to have a set of parameters that could fit all cases, even approximately. We had to separate the laboratory scale tests from the field scale and real fire cases. One possible reason may be the variation in the residence time value in both sets of cases.

As seen in Figs 4 and 5, some points do not follow the trend of model prediction in some ranges of variation. This is the case, for example, in the canyon and junction fire tests, which show a higher acceleration than that predicted by the average model. This indicates that, under certain boundary conditions, such as terrain and fire line configuration, other parameters sets should be used for a more accurate description of fire behaviour.

Practical application of the model

The proposed model can be applied in practical operations; both to analyse and interpret fire behaviour in acceleration and deceleration phases and to predict the amplitude and duration of each phase. This is very relevant in fire management operations as it provides information about the maximum values of the ROS that can be expected in an accelerating fire and the time lapse it will take.

In Fig. 8 curves of $Δ t_{a} = (Δ t_{d})$ as a function of $Δ R_{a}^{'} \times (Δ R_{d}^{'})$ for given values of $Δ R_{1}^{'} \times (Δ R_{3}^{'})$ are shown. From these, or similar curves, knowing the initial values of $Δ R_{1}^{'} \times (Δ R_{3}^{'})$ it is possible to estimate the time lapses $Δ t_{a} = (Δ t_{d})$ required to achieve a given variation of $Δ R_{a}^{'} \times (Δ R_{d}^{'})$ ).

For acceleration: $Δ R_{a}^{'} = R_{2}^{'} - R_{1}^{'} and Δ t_{a} = t_{2} - t_{1}$
For deceleration: $Δ R_{d}^{'} = R_{4}^{'} - R_{3}^{'} and Δ t_{d} = t_{4} - t_{3}$ .

Fig. 8.

Time delays predicted by the analytical model for (a) acceleration and (b) deceleration phases of wildfires for given values of the initial values of R′₁ or R′₃.

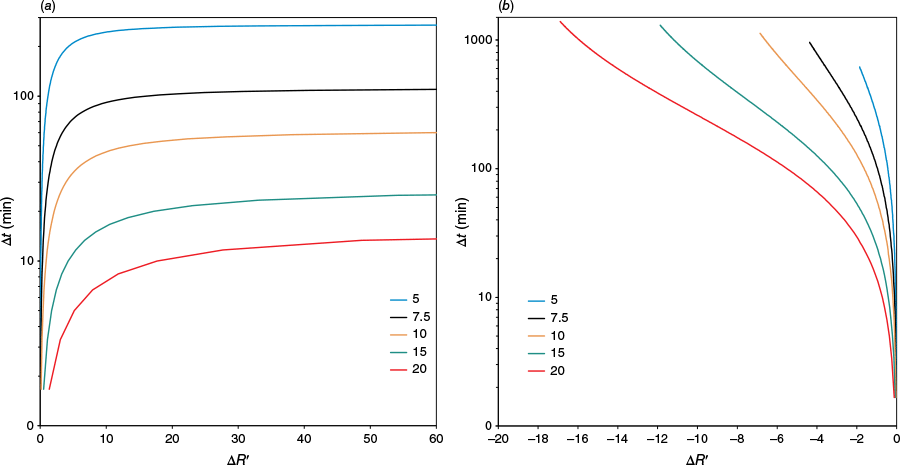
For example, for a given fire, if we know the value of $R_{1}^{'}$ and assume that the fire will reach a value of $R_{2}^{'}$ , using the present model it is possible to estimate the time that the fire will take to reach its peak value. By integrating the function R(t) in the present model, it is also possible to estimate the distance that the fire will travel during its acceleration. This information can be used to avoid deployment of resources in the path of the fire during its acceleration. Analysing the corresponding deceleration period that will follow the acceleration, it will be possible to plan with anticipation where and when the fire ROS will reach its minimum value, so that resources can be deployed either to rescue personnel or to attempt to stop the fire.

Using current fire behaviour models, like Behave (Andrews 1986), recently known as Behave Plus (Andrews 2014), we can estimate R₀ and R₁, and so $R_{1}^{'}$ , but at present we do not have complete information to estimate $R_{2}^{'}$ , or even $Δ R_{a}^{'}$ . Viegas et al. 2021 showed that in large fires, the ratio between R₂ and R₁ can be of the order of 2–5, depending on the dimension of the fire. On the other hand, the present data, based on a limited but relevant collection of large fires, show that $Δ R_{a}^{'}$ varied between 20 and 50. In the absence of more accurate data or better prediction methods, these two indicators can be used to obtain a first estimate of the order of magnitude of the parameters required for operations, allowing for more efficient and safer resource management.

Conclusion

In the present paper an analytical model to predict the head fire front acceleration and deceleration phases that are observed in the majority of fires at all scales is proposed. This model considers the effect of the convective flow induced by the fire in its surrounding atmosphere, identifying two development phases according to the relative magnitude of the characteristic flow velocity on each side of the fire front. The model is applied to the accelerating phase during which the ROS of the fire starts from an initial value, that depends on the boundary conditions and increases till reaching a maximum value that depends on the overall fire conditions. The same analytical model, with adequate parameters, describes the deceleration phase as well, reasonably predicting the fast decrease of the ROS observed in all types of fires. Using data from a wide set of experimental and wildfires, two sets of model parameters for laboratory and field scale fires were proposed to provide a first order prediction of the temporal variation of the ROS in the general case. In future work, model parameters to predict more accurately the fire spread variation in particular cases, like canyon or junction fires, shall be proposed.

The model explains the large variations of a fire’s non-dimensional ROS, which can have positive or negative variations of 50, 100 or more, even in nominally permanent boundary conditions. These time-dependent changes are produced by the fire-induced convection and cannot be explained by temporal variation of the factors included in the ‘classical fire environment triangle’.

In the case of wildfires, the model was used to estimate the time delays required to observe certain changes in the ROS, given the fire’s initial conditions. Although a single curve was used to fit all cases, the accuracy achieved appears to be sufficient for most practical and operational applications.

There are still several aspects of the present study that require further investigation, to allow a generalised and more accurate application of the model. In the first place, the basic parameters of the model, like the residence time and the basic ROS of the fuel bed, must be determined, either using adequate models or experimental results. The same happens to the coefficients of the model. Here we used a set of values that were measured carefully for laboratory experiments but are only rough estimates for the wildfires. The initial values of R′₁ of an acceleration phase can be determined using static fire prediction models, but at present we do not know how to estimate R′₂. Possibly using a larger database of wildfires and analysing their boundary conditions, it will be feasible to feed the model with such parameters to allow its application in more general cases. The same happens for the deceleration phase with R′₃ and R′₄. This is also left for future work.

The present model offers a relatively simple analytical solution to account for the effect of the fire-induced convection on fire spread. It constitutes an innovative approach to interpreting the mechanism of dynamic fire spread, with broad potential for development and application. It is expected that it will also contribute to change some well imbedded but incorrect concepts like those of the ‘classical fire environment triangle’ and of ‘wind’ or ‘convection’ dominated fires, that do not explain the acceleration and deceleration of the head fires that is observed frequently and help to recognise that they are a result mainly of the self-induced effect of the dynamic interaction between the fire and its environment.

Symbols

R_i	Rate of spread in the time t_i (cm s⁻¹)
t_i	Initial time (s)
R₁ and R₂	Rate of spread during the acceleration phase in the time t₁ and t₂ (cm s⁻¹)
t₁ and t₂	Time that corresponds the Rate of spread R₁ and R₂ during the acceleration phase
R_max	Maximum Rate of spread in the time t_max (cm s⁻¹)
t_max	Time that corresponds the maximum ROS (s)
R₃ and R₄	Rate of spread during the deceleration phase in the time t₃ and t₄ (cm s⁻¹)
t₃ and t₄	Time that corresponds the Rate of spread R₃ and R₄ during the deceleration phase
R_o	Basic rate of spread (cm s⁻¹)
R	Rate of spread (ROS) (cm s⁻¹)
R′	Non-dimensional ROS
U_o	Reference flow velocity (m s⁻¹)
U	Flow velocity near the fire front (m s⁻¹)
U′	Non-dimensional flow velocity
U₁	Characteristic flow velocity on the windward side (m s⁻¹)
U₂	The reverse flow on the opposite side of the fire front, on the leeward side (m s⁻¹)
t_o	Residence time of the fire in the fuel bed (s)
t	Time elapsed since the start of the fire (s)
t′	Non-dimensional time
t^*	Modified time scale (s)
$t_{i}^{' ⁎}$	The values of $t_{i}^{' ⁎}$ are measured in the physical scale of a given experiment or of a real case.
a₁	Parameter a₁ considered in the mathematical model of the R′ can be empirically determined
a₂	Parameter a₂ considered in dU′ the local velocity in an infinitesimal period of time dt can be empirically determined
a₃	Parameter a₃ considered in dU the local velocity during the deceleration phase in an infinitesimal period of time dt can be empirically determined
$a_{1}^{'}, a_{2}^{'} and a_{3}^{'}$	Non-dimensional parameters
b₁	Parameter b₁ considered in the mathematical model of the R′ can be empirically determined
b₂	Parameter b₂ considered in dU′ the local velocity in an infinitesimal period of time dt can be empirically determined
b₃	Parameter b₃ considered in dU the local velocity during the deceleration phase in an infinitesimal period of time dt can be empirically determined
dU′	The local velocity in an infinitesimal period of time dt (m s⁻¹)
dt	Infinitesimal period of time (s)
α	Slope angle (°)
m_f	Moisture content of the fuel bed particles (dry basis)

Data availability

Data are available by request to the corresponding author: xavier.viegas@dem.uc.pt

Conflicts of interest

Domingos Xavier Viegas and Miguel Almeida are Guest Editors of the International Journal of Wildland Fire but were not involved in the peer review or any decision-making process for this paper. The authors declare no other conflicts of interest.

Declaration of funding

This research was funded in part by the Fundação para a Ciência e a Tecnologia, I.P. (FCT, https://ror.org/00snfqn5816) under Grant UIDB/50022/2020 (https://doi.org/10.54499/UIDB/50022/2020); UIDP/50022/2020 (https://doi.org/10.54499/UIDP/50022/2020); LA/P/0079/2020 (https://doi.org/10.54499/LA/P/0079/2020). For the purpose of Open Access, the author has applied a CC-BY public copyright license to any Author‘s Accepted Manuscript (AAM) version arising from this submission.

This research work was funded and carried out within the scope of the following projects: (1) FirEUrisk project - Developing a Holistic, Risk-Wise Strategy for European Wildfire Management, which received funding from the European Union’s Horizon 2020 research and innovation programme under the grant agreement No. 101003890; (2) project Large Fires funded by FCT — Foundation for Science and Technology with reference COMPETE2030-FEDER-00878700.

Acknowledgements

The support given by Agenda TransForm, (PRR 02/C05-i01/2022), namely through project ‘CENTRODEC’ (Centro de Apoio à Decisão com Dados Multisensoriais para a Proteção da Floresta), with the contract of Carlos Ribeiro, is gratefully acknowledged. The support given by Nuno Luís and João Carvalho in performing the laboratory experiments is gratefully acknowledged.

Author contributions

Conceptualisation: Domingos Xavier Viegas and Carlos Ribeiro. Data curation: Carlos Ribeiro. Formal analysis: Domingos Xavier Viegas and Carlos Ribeiro. Methodology: Domingos Xavier Viegas and Carlos Ribeiro. Experimental test: Domingos Xavier Viegas, Carlos Ribeiro, Luís M. Ribeiro, Miguel Almeida, Tiago Rodrigues and Thiago Fernandes Barbosa. Supervision: Domingos Xavier Viegas. Writing – original draft: Domingos Xavier Viegas and Carlos Ribeiro. Writing – review & editing: Domingos Xavier Viegas, Carlos Ribeiro, Luís M. Ribeiro, Miguel Almeida, Tiago Rodrigues and Thiago Fernandes Barbosa.

References

Anderson HE (1968) Fire spread and flame shape. Fire Technology 4(1), 51-58.
| Crossref | Google Scholar |

Andrews PL (1986) BEHAVE: Fire Behavior Prediction and Fuel Modeling System-BURN Subsystem, Part 1, U.S. Department of Agriculture, Forest Service, Intermountain Research Station. General Technical Report INT-194. (Ogden, UT)

Andrews PL (2014) Current status and future needs of the BehavePlus Fire Modeling System. International Journal of Wildland Fire 23(1), 21.
| Crossref | Google Scholar |

Cliff EP, Price JH, Lindh CO, Mays LK, Cochran HD (1953) The Rattlesnake Fire, U.S. Department of Agriculture, Forest Service.

Countryman CM (1972) ‘The Fire Environment Concept.’ (USDA Forest Service, Pacific Southwest Forest and Range Experiment Station: Berkeley, CA)

Donoghue L, Kackson G, Angel R, Beebe G, Bishop K, Close K, Moore R, Newman E, Schmidt M, Whitlock C (2003) Cramer Fire Fatalities. Accident Investigation Factual Report. U.S. Department of Agriculture, Forest Service, North Fork Ranger District, Slamon-Challis National Forest, Region 4, Salmon.

Filkov AI, Duff TJ, Penman TD (2020) Frequency of dynamic fire behaviours in australian forest environments. Fire 3(1), 1-17.
| Crossref | Google Scholar |

Finklin AI (1973) Meteorological Factors in the Sundance Fire run. Intermountain Forest and range Experiment Station. U.S. Dept. of Agriculture, Forest Service, Intermountain Forest and Range Experiment Station. (Ogden, Utah)

Finney MA, Cohen JD, Forthofer JM, McAllister SS, Gollner MJ, Gorham DJ, Saito K, Akafuah NK, Adam BA, English JD (2015) Role of buoyant flame dynamics in wildfire spread. Proceedings of the National Academy of Sciences 112(32), 9833-9838.
| Crossref | Google Scholar | PubMed |

Haynes K, Short K, Xanthopoulos G, Viegas D, Ribeiro LM, Blanchi R (2020) Wildfires and WUI Fire Fatalities. In ‘Encyclopedia of Wildfires and Wildland-Urban Interface (WUI) Fires.’ (Ed. S Manzello) pp. 1–16. (Springer International Publishing: Cham, Switzerland)

Nelson RM, Jr (2003) Power of the fire—a thermodynamic analysis. International Journal of Wildland Fire 12(1), 51.
| Crossref | Google Scholar |

Pinto P, Silva ÁP, Viegas DX, Almeida M, Raposo J, Ribeiro LM (2022) Influence of convectively driven flows in the course of a large fire in Portugal: the case of Pedrógão Grande. Atmosphere 13(3), 414.
| Crossref | Google Scholar |

Raposo J, Viegas DX, Xie X, Almeida M, Naian L (2014) Analysis of the jump fire produced by the interaction of two oblique fire fronts: comparison between laboratory and field cases. In ‘Advances in Forest Fire Research’. (Ed. DX Viegas) pp. 88–94. (Imprensa da Universidade de Coimbra: Portugal)

Raposo JR, Cabiddu S, Viegas DX, Salis M, Sharples J (2015) Experimental analysis of fire spread across a two-dimensional ridge under wind conditions. International Journal of Wildland Fire 24(7), 1008-1022.
| Crossref | Google Scholar |

Raposo JR, Viegas DX, Xie X, Almeida M, Figueiredo AR, Porto L, Sharples J (2018) Analysis of the physical processes associated with junction fires at laboratory and field scales. International Journal of Wildland Fire 27(1), 52-68.
| Crossref | Google Scholar |

Ribeiro C (2024) ‘Analysis of the Interaction Between Fire Fronts in Complex Topography.’ (University of Coimbra: Coimbra, Portugal)

Ribeiro C, Reis L, Raposo J, Rodrigues A, Viegas DX, Sharples J (2022) Interaction between two parallel fire fronts under different wind conditions. International Journal of Wildland Fire 31(5), 492-506.
| Crossref | Google Scholar |

Ribeiro C, Xavier Viegas D, Raposo J, Reis L, Sharples J (2023) Slope effect on junction fire with two non-symmetric fire fronts. International Journal of Wildland Fire 32(3), 328-335.
| Crossref | Google Scholar |

Rodrigues A, Ribeiro C, Raposo J, Viegas DX, André J (2019) Effect of canyons on a fire propagating laterally over slopes. Frontiers in Mechanical Engineering 5, 41.
| Crossref | Google Scholar |

Rodrigues A, Viegas DX, Almeida M, Ribeiro C, Raposo J, André J (2023) Fire propagating laterally over a slope with and without an embedded canyon. Fire Safety Journal 138, 103791.
| Crossref | Google Scholar |

Rothermel RC (1972) A mathematical Model for Predicting Fire Spread in Wildland Fuels. USDA Forest Service, Intermountain Forest and Range Experiment Station, Research Paper INT-RP-115. (Ogden, UT)

Rothermel RC (1983) How to Predict the Spread and Intensity of Forest and Range Fires. U.S. Department of Agriculture, Forest Service, Intermountain Forest and Range Experiment Station, General Technical Report INT-143. (Ogden, UT)

Rothermel RC (1991) Predicting Behavior and Size of Crown Fires in the Northern Rocky Mountains. U.S. Department of Agriculture, Forest Service, Intermountain Research Station, Res. Pap. INT-RP-438. (Ogden, UT)

Santoni PA, Balbi JH, Dupuy JL (2000) Dynamic modelling of upslope fire growth. International Journal of Wildland Fire 9(4), 285-292.
| Crossref | Google Scholar |

Simard A, Haines D, Blank R, Frost J (1983) The Mack Lake Fire. USDA Forest Service, North Central Forest Experiment Station, General Technical Report NC-83. (St Paul, MN). 10.2737/NC-GTR-83

Thomas CM, Sharples JJ, Evans JP (2015) Pyroconvective interaction of two merged fire lines: curvature effects and dynamic fire spread. In ‘MODSIM2015, 21st International Congress on Modelling and Simulation’. Gold Coast, Australia, 29 November, 2015. (Eds Weber T, McPhee MJ, Anderssen RS) pp. 312–318. (Modelling and Simulation Society of Australia and New Zealand: Gold Coast, Australia)

Viegas X (2004) A mathematical model for forest fires blowup. Combustion Science and Technology 177(1), 27-51.
| Crossref | Google Scholar |

Viegas DX (2006) Parametric study of an eruptive fire behaviour model. International Journal of Wildland Fire 15(2), 169.
| Crossref | Google Scholar |

Viegas DX, Pita LP (2004) Fire spread in canyons. International Journal of Wildland Fire 13(3), 253-274.
| Crossref | Google Scholar |

Viegas DX, Cruz MG, Ribeiro LM, Silva AJ, Ollero A, Arrue B, Dios R, Gómez-Rodrígues F, Merino L, Miranda AI, Santos P (2002) Gestosa fire spread experiments. In ‘Proceedings of the 4th International Conference on Forest Fire Research and Wildland Fire Safety’. Luso. (Ed. DX Viegas) (Millpress)

Viegas D, Raposo J, Figueiredo A (2013) Preliminary analysis of slope and fuel bed effect on jump behavior in forest fires. Procedia Engineering 62, 1032–1039, 10.1016/j.proeng.2013.08.158

Viegas D, Almeida M, Ribeiro M, Raposo J, Viegas M, Oliveira R, Alves D, Pinto C, Jorge H, Rodrigues A, Lucas D, Lopes S, Silva F (2017) O Complexo de Incêndios de Pedrógão Grande e Concelhos Limítrofes, Iniciado a 17 de Junho de 2017. Available at https://www.portugal.gov.pt/download-ficheiros/ficheiro.aspx?v=%3d%3dBAAAAB%2bLCAAAAAAABAAzNjU1AwAH%2bPGMBAAAAA%3d%3d

Viegas DX, Almeida MA, Ribeiro LM, Raposo J, Viegas MT, Oliveira R, Alves D, Pinto C, Rodrigues A, Ribeiro C, Lopes S, Jorge H, Viegas CX (2019) ‘Análise dos Incêndios Florestais Ocorridos a 15 de outubro de 2017.’ (Centro de Estudos sobre Incêndios Florestais (CEIF/ADAI/LAETA)) [In Portuguese]

Viegas X, Raposo J, Ribeiro C, Reis L, Abouali A, Viegas C (2021) On the non-monotonic behaviour of fire spread. International Journal of Wildland Fire 30(9), 702-719.
| Crossref | Google Scholar |

Viegas X, Raposo J, Ribeiro C, Reis L, Abouali A, Ribeiro LM, Viegas C (2022) On the intermittent nature of forest fire spread – Part 2. International Journal of Wildland Fire 31(10), 967-981.
| Crossref | Google Scholar |

Viegas X, Ribeiro C, Almeida M, Pinto P, Ribeiro LM, Silva Á (2023) Field and laboratory analysis of the junction fire process in the catastrophic fire of Pedrógão Grande in June 2017. International Journal of Wildland Fire 32, 951-967.
| Crossref | Google Scholar |

Viegas DX, Ribeiro C, Barbosa TF, Rodrigues T, Ribeiro LM (2024) A fireline displacement model to predict fire spread. Fire 7(4), 121.
| Crossref | Google Scholar |

Wade DD, Ward DE (1973) An Analysis of the Air Force Bomb Range Fire. Res. Pap. SE-105. 41 p. (U.S. Department of Agriculture, Forest Service, Southeastern Forest Experiment Station: Asheville, NC)

Wotton BM, Gould JS, McCaw WL, Cheney NP, Taylor SW (2012) Flame temperature and residence time of fires in dry eucalypt forest. International Journal of Wildland Fire 21(3), 270-281.
| Crossref | Google Scholar |

Xie X, Liu N, Viegas DX, Raposo JR (2014) Experimental Research on Upslope Fire and Jump Fire. 10.3801/IAFSS.FSS.11-1430

Xie X, Liu N, Raposo JR, Viegas DX, Yuan X, Tu R (2020) An experimental and analytical investigation of canyon fire spread. Combustion and Flame 212, 367-376.
| Crossref | Google Scholar |