A statistical model for predicting water temperature in temperate rivers and streams
Patricia Y. Koh A * , Jian D. L. Yen B , Jarod P. Lyon B , Matt West A and John R. Morrongiello
A * , Jian D. L. Yen B , Jarod P. Lyon B , Matt West A and John R. Morrongiello  A
A
A
B
Abstract
Water temperature affects the biology and ecology of many freshwater species. However, in situ water temperature measurements are not always available because of spatial or temporal gaps in observations.
We evaluated the importance of different environmental variables in predicting water temperature in temperate Australian rivers and streams and developed a water temperature model for use in these environments.
We used linear mixed models that incorporated combinations of air temperature, stream flow and catchment variables to predict daily water temperatures.
Air temperature integrated over the preceding 7 days, in conjunction with elevation, were very good predictors of water temperature. However, stream flow did not significantly improve model predictions.
Air temperature explained the most variation in water temperature, and elevation also improved model predictions.
Our approach demonstrated that water temperature in temperate rivers and streams can be readily modelled using elevation and air temperature across large spatial and temporal scales. Our work has provided an easily implementable method to fill gaps in monitoring networks in temperate climate zones exhibiting warm summers. The predictions created by our model will have most use in studies where researchers want to explore the impacts of relative changes in water temperature.
Keywords: air temperature, Australia, elevation, freshwater, lotic, river temperature, statistical models, stream temperature, water temperature.
Introduction
Water temperature is of profound importance to the biology and ecology of freshwater ecosystems (Morrongiello et al. 2011; Ohlberger 2013; Riemer et al. 2018; Zhao et al. 2023; Shackleton et al. 2024). However, despite its significance, continuous in situ measurements of water temperature are often not available. Where measurements are taken, time series of water temperature are often measured using in-stream electronic data sensors (e.g. Dunham et al. 2005; Isaak and Horan 2011). Unfortunately, limited resources or malfunctioning equipment can interrupt an otherwise continuous time series of data (Arismendi et al. 2013), and spatial gaps can occur because of the challenging task of installing water temperature instruments across river systems or the costs of developing and maintaining large monitoring networks (Benyahya 2014). Remote-sensing approaches to quantify freshwater temperatures do offer some promise; however, the satellite-derived techniques commonly used in sea-surface temperature estimates lack the resolution required for freshwater systems (O’Carroll et al. 2019), and helicopter- and aeroplane-mounted thermal infrared remote sensing can be costly and challenging to deploy at the required temporal and spatial scale (Torgersen et al. 2001; Dugdale et al. 2019). Air temperature is often used to overcome spatial and temporal gaps in logging histories, given it is highly correlated with water temperature (e.g. Buisson et al. 2008; Woods et al. 2023). Novel analyses of high quality extrapolated gridded air temperature products, such as fifth generation of the European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis (ERA5) (Hersbach et al. 2023) and the USA-based product for gridded air temperature estimates (Daymet V4) (Thornton et al. 2021), offer an exciting opportunity to predict time series of water temperature across the riverscape away from existing monitoring infrastructure (e.g. Gatien et al. 2023). The correlation of air temperature and water temperature generally approximates the heat exchange between the surrounding atmosphere and water (Webb et al. 2003). Deviations in this relationship can occur because of how hydrology affects heat transfer both at the air–water interface and throughout the waterbody itself. For example, air temperature can have a temporally delayed or lagged relationship with water temperature (Stefan and Preud’homme 1993), influenced by both the thermal properties of water and how hydrology alters channel morphology and flow regime of a watercourse (Letcher et al. 2016). Likewise, in large watercourses, where there is relatively low surface area but high volume compared to small watercourses, water temperature takes longer to equilibrate with the surrounding air temperature because of low energy transfer at the air–water interface and increased overall thermal capacity (Webb et al. 2003). Flow regimes can also affect the rate of energy transfer through turbulence and stratification. Reduced water movement creates higher levels of stratification because of lower turbulence. This stratification reduces the rate of heat transfer (Booker and Whitehead 2022). By contrast, faster water movement causes more turbulence, which in turn reduces stratification and increases the rate of heat transfer. However, how channel morphology and flow regime interact to affect the rate of heat transfer is not always clear. For example, small watercourses with high rates of discharge do not necessarily adhere closely to air temperature, presumably because of both increased thermal capacity owing to increased volume, and reduced time exposure to surrounding air temperature (Smith and Lavis 1975). Thus, it is important to consider hydrological characteristics when predicting water temperature, given their role in modulating the rate of heat exchange with the surrounding atmosphere.
Environmental predictors other than air temperature and hydrology may also influence water temperature (Caissie 2006). For example, riparian vegetation can shade a waterbody from solar radiation and, consequently, moderate high temperatures (Broadmeadow and Nisbet 2004; Garner et al. 2014; Abdi and Endreny 2019), whereas surrounding land use can affect local humidity and thus stream evaporation rates (Te Wierik et al. 2021). Likewise, stream orientation determines the duration and quantity and the timing of solar radiation to which a stream is exposed and thus its temperature (Garner et al. 2017). High-elevation watercourses generally have smaller catchments and thus smaller water volumes, whereas low-elevation watercourses generally have larger catchments and thus larger volumes. The water temperature of relatively high-elevation sites might also be disproportionately affected by cold-water inputs of snow melt and ground water compared with low-elevation sites (Lisi et al. 2015; Somers and McKenzie 2020). Data for many of these topographical factors may be available and can be harnessed to improve predictions of water temperature.
Previous attempts to predict water temperature from other environmental data have adopted either a deterministic, process-based approach (see Dugdale et al. 2017) or a correlative, statistically based, approach (see Benyahya et al. 2007). Deterministic models have a predictive advantage in that they solve fundamental heat exchange equations to estimate water temperatures and they can include reach-specific data including stream geometry to capture mechanistic underpinnings (Dugdale et al. 2017). However, these advantages come at a computational and data requirement cost (Hébert et al. 2015; Dugdale et al. 2017). By contrast, statistical approaches, based on either regression or machine learning models, often have fewer data needs and so can be applied across the entire landscape (Benyahya et al. 2007). Regression models require the user to stipulate the model structure and can be as simple as a linear model of the air–water temperature relationship (Stefan and Preud’homme 1993) to more complex models that incorporate hydrology, temporal delays, seasonality and catchment-scale covariates (Webb et al. 2003; Ahmadi-Nedushan et al. 2007; Rosencranz et al. 2021; Struthers et al. 2024). Machine learning models, such as those based on artificial neural networks (Zhu and Piotrowski 2020; Zhi et al. 2023), rely on the input data to drive model structure and thus often have higher predictive power than have regression models. However, machine learning models do tend to overfit data and, so, even though their hindsight predictive performance is better than that of regression models, they may not be suitable for forecast predictions (Benyahya et al. 2007). The degree of model accuracy required is also dependent on the end use of the data product: many ecological studies require only a relative index of water temperature, whereas eco-physiological studies might require more absolute temperature values to link to experimental data.
In this study, we aim to predict daily freshwater temperature across rivers and streams in Victoria, Australia, by using a statistical hierarchical regression approach. Our study region has an extensive river gauging network (Bureau of Meteorology, see http://www.bom.gov.au/waterdata) because of a history of drought and floods and the legislated requirement for a coordinated monitoring network to manage water resources for the environment, human consumption and agriculture (Victorian Water Act 1989). However, water temperature is only sporadically recorded, or not recorded at all, at many of these monitoring sites, resulting in a paucity of continuous observed water temperature measurements. We explore three inter-related questions relating to the development of physical parameters to include in regression models, and their subsequent impact on predictive performance.
What is the relative importance of air temperature and stream flow in predicting daily water temperature, and what time lags or integration times for these parameters explain the most variation?
Does the inclusion of catchment characteristics improve model performance?
Is model performance significantly improved when both air temperature and stream flow are included?
Our study generates an analytical framework that can be applied across similar hydrological and climatic conditions in south-eastern Australia and, more generally, provides insight to global users about the value of air temperature, stream flow and other site characteristics in predicting water temperature.
Materials and methods
Study area
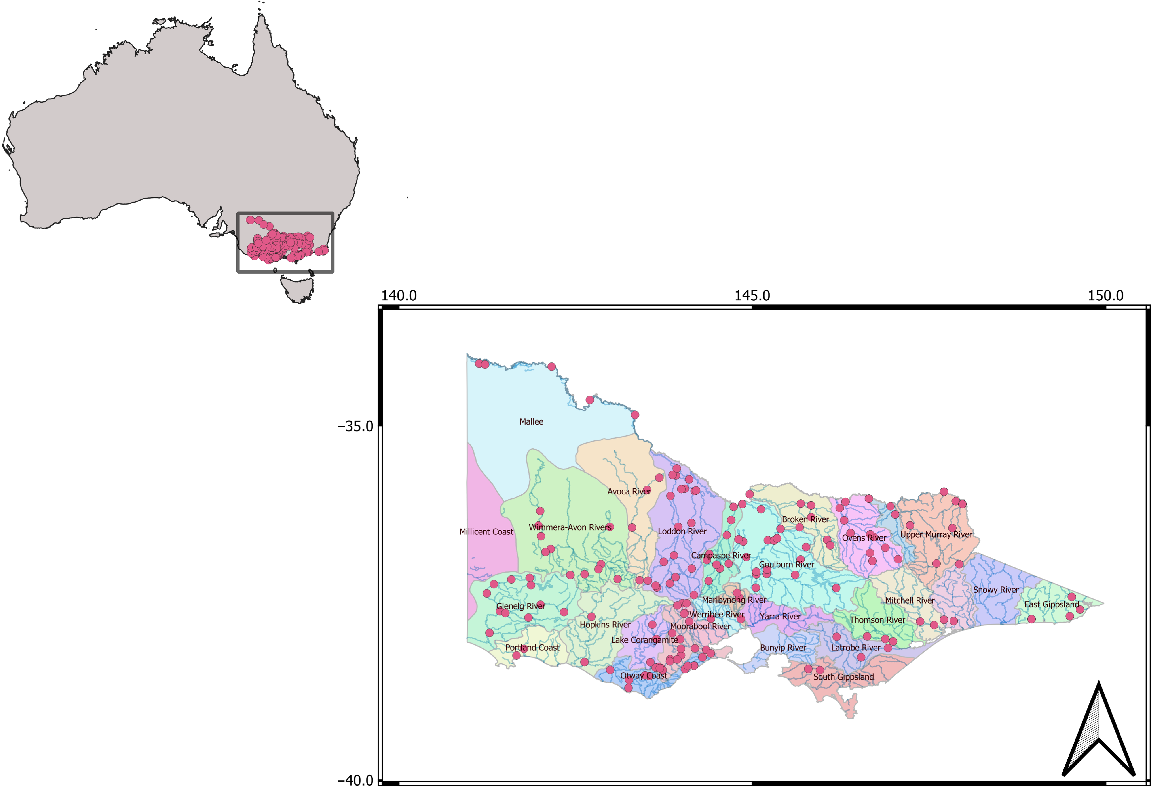
Our study focussed on predicting water temperatures for rivers and streams within Victoria, a state in south-eastern Australia (Fig. 1). This study area contains watercourses in 29 drainage basins across an area of 227,444 km2. Drainage basins differ in their topography, climate, hydrology, groundwater reliance and land-use (Land Use Victoria 2023).
Location of stream gauging stations (red points), drainage basins (coloured polygons) and major waterways (blue lines) in Victoria, Australia (inset). Figure was created using QGIS (ver. 3.36.2, see https://github.com/qgis/QGIS). Note that there are very few water courses in north-western Victoria and thus there are no gauges present in this area.
Victoria predominantly experiences a temperate climate and, hence, most of Victoria experiences warm summers and cold winters, although higher-altitude areas have mild summers and semi-arid areas experience hot dry summers (Peel et al. 2007; Bureau of Meteorology 2017). Rainfall in south-eastern Australia is seasonal but can be inconsistent (Nicholls et al. 1997) and is often linked to the El Nino Southern Oscillation (ENSO), with El Nino years resulting in warm dry years and La Nina years resulting in cool wet years (Hauser et al. 2020). Consequently, the hydrology of Victoria’s rivers and streams can display high inter-annual variability and many are characterised by periods of intermittent flow (Kennard et al. 2010). Thus, this study area encompasses rivers and streams with extreme winter-dominant, moderate-winter, early-spring and moderate-autumn seasonal river regimes (Finlayson and McMahon 1988). Stream attributes, such as channel depth and width, and riparian vegetation cover, are unknown for most of the stream network and so this precluded an exploration of deterministic water temperature model approaches.
Accessing environmental data
All environmental data were collated and analysed using the program R (ver. 4.3.1, R Foundation for Statistical Computing, Vienna, Austria, see https://www.r-project.org/) and RStudio (ver. 2023.09.0, Posit Software, PBC, Boston, MA, USA, see https://posit.co/products/open-source/rstudio/).
We downloaded hourly resolved 0.25 by 0.25 degree spatially gridded air temperature data centred on each gauge location from ERA5 climate datasets (Hersbach et al. 2023), by using the mcera5 package (ver. 0.3.0, see https://github.com/dklinges9/mcera5; Klinges et al. 2022). This air temperature data were averaged across cells centred on the gauge location to attain a time series of mean daily temperature for each gauge. Daily mean water temperature (°C), mean daily stream flow (ML day−1) measurements and site details were downloaded from the Department of Energy, Environment and Climate Action’s Water Measurement Information System (see https://data.water.vic.gov.au) for all available gauges within Victoria. Site details included drainage basin and upstream catchment area for most gauges. Where this information was not available, we removed this site from the dataset. The elevation of each gauge was downloaded using the elevatr package (ver. 0.99.0, see https://CRAN.R-project.org/package=elevatr; Hollister et al. 2023). Air temperature, stream flow and site details were merged into an environmental predictor data frame. We excluded data from any gauges that were placed on drains, large dams, large reservoirs or tail races because these forms of river regulation are known to affect water temperature (Erickson and Stefan 2000; Moore 2006) and thus not be comparable to data from the majority of sites that experience more natural flow regimes.
The available water temperature dataset has not been formally cleaned to remove recording errors and so we undertook a series of steps to help ensure data quality. First, we filtered out extreme water temperature records above 50°C and below 1°C, because these are implausible for Victorian conditions. Second, we filtered out data that were greater than three standard deviations away from the annual mean value of the gauge, because these data are likely to represent erroneous recordings. Last, we visually inspected the observed water temperature record for all gauges to detect potential anomalies. We identified such potentially erroneous data recordings in 21 of 232 gauges. These were identified as dramatic drops or rises in temperature over a short time, or periods lacking temporal variation that may indicate a faulty sensor. We manually removed these periods in 17 gauges (removed data are shown in Supplementary Fig. S1–S17), whereas four gauges were omitted entirely because of large periods of potentially erroneous data. Overall, our filtering removed 27,260 extreme or potentially erroneous daily water temperature observations, representing 2.81% of the total data set. The cleaned water temperature data were merged with site details. We omitted gauges from three river basins (Bunyip River, Millicent Coast and the Snowy River) because of an absence of all required environmental predictors at each location. This resulted in a final sample size of 692,646 daily observations of water temperature from 164 gauges across 26 drainage basins, with an average of 422.5 days of data per gauge (90–10,702 days). Our data spanned the period 1979–2022 because this was the temporal extent of available air temperature estimates at the time of analysis.
Predictor variable development, model structure and validation
All environmental predictors (air temperature, stream flow, catchment area and gauge elevation) were normalised to facilitate model fitting and improve parameter estimation. The response variable, water temperature, was square-root transformed to conform to distributional assumptions. We considered six different lagged and rolling mean terms to explore the temporal effect of air temperature and stream flow on water temperature on a given day. These were the air temperature or stream flow of the target day (meanDailyAir and meanDailyFlow), the air temperature or stream flow of the day prior to the target day (lagAir_1 and lagFlow_1), and the air temperature or stream flow of the day 2 days prior to the target day (lagAir_2 and lagFlow_2), the average air temperature and stream flow of the 2 days preceding the target day (rollAir_2 and rollFlow_2), the average air temperature and stream flow of the 7 days preceding the target day (rollAir_7 and rollFlow_7) and the average air temperature and stream flow of the 14 days preceding the target day (rollAir_14 and rollFlow_14). Our inclusion of lagged and time-averaged predictor variables allowed us to explore the importance of a range of time periods suggested as being important in predicting water temperature (Van Vliet et al. 2011; Rosencranz et al. 2021).
Water temperature was modelled using linear mixed effects models fit with the lme4 package (ver. 1.1–34, see https://CRAN.R-project.org/package=lme4; Bates et al. 2015). These models included random intercepts for gauge nested within drainage basin to allow for the hierarchical structure of daily water temperature observations and to account for the possibility that gauges within a drainage basin experience more similar climatic, hydrological and geological conditions than do gauges located in different drainage basins.
To address our research questions, we fit three model suites that incorporated different combinations of air temperature, stream flow and catchment-characteristic predictor variables, including both linear and quadratic terms for air temperature and stream flow (Table 1). Our first suite of models compared the 12 different lagged and rolling mean terms for air temperature and stream flow. This model suite allowed us to identify the most important air temperature and stream flow predictors from our candidate set, which were then used in subsequent models. Our second suite of models included the best air temperature or stream flow predictor in addition to catchment characteristics. Finally, our third model suite included the best air temperature, stream flow, and catchment characteristics together. We included only one type of temperature or flow predictor variable in any single model because of collinearity between these variables. Further, gauge elevation and catchment area were included in separate models because these are not independent catchment characteristics (Fig. S18).
| Item | Maximal model | |
|---|---|---|
| Null model | Water temperature ~ (1|drainage basin/gauge) | |
| 1. Air temperature only or stream flow only suite | Water temperature ~ air temperature predictor + air temperature predictor2 + (1|drainage basin/gauge) Water temperature ~ stream flow predictor + stream flow predictor2 + (1|drainage basin/gauge) | |
| 2. Air temperature or stream flow and catchment characteristics suite | Water temperature ~ air temperature predictor + air temperature predictor2 + catchment characteristic + (1|drainage basin/gauge) Water temperature ~ stream flow predictor + stream flow predictor2 + catchment characteristic + (1|drainage basin/gauge) | |
| 3. Air temperature, stream flow and catchment characteristics suite | Water temperature ~ air temperature predictor + air temperature predictor2 + stream flow predictor + stream flow predictor2 + catchment characteristic + (1|drainage basin/gauge) |
Only one term for each predictor was used in each competing model, i.e. lagAir_1 or rollAir_7 to represent air temperature, but not both. Only one catchment characteristic, either upstream catchment area or gauge elevation, was included in each model. Random effects were included in all models to allow for observations to be nested within sites, which themselves were nested within drainage basins.
The optimum duration for different periods of time-lagged air temperatures to predict water temperature has been explored elsewhere, with the optimal lag duration shown to increase with stream depth (Stefan and Preud’homme 1993) and with stream flow (Van Vliet et al. 2011). We allowed for an interaction between air temperature and stream-flow, but did not allow for the duration of the air temperature lag to vary with stream flow. By selecting a universal integration period duration, we produced a more generalised model that has utility across a wide range of sites where flow data might not be present.
Competing models were fit by using maximum likelihood, and their relative performance was ranked using two common measures of goodness-of-fit, namely, the coefficient of determination (R2) and root mean square value (RMSE), given by Eqn 1 and 2 respectively.
RMSE is a measure of the difference between predicted and observed values for a given model. Models with lower RMSE have a lower degree of error between predicted and observed values, whereas models with a higher RMSE have a high degree of error between those values. R2 and RMSE values were calculated for each model. This allowed us to determine the relative importance of a variable within a model suite, as well as the overall performance of each model globally.
We used blocked, 10-fold cross-validation to assess the predictive power of our models against observed water temperature. This was performed by splitting our data set into ten blocks (~69,264 observations per block), with nine blocks being used to train the model and one block used to test the model at each iteration (i.e. fold). Data were stratified by entire gauges to ensure that the model was tested against novel gauges not included in model fitting. This approach represents the realistic scenario where a practitioner wants to predict water temperature at a completely new site where no water temperature data are available. Training data were used to refit each model and predicted values were calculated and compared with observed water temperature in the testing data set. The coefficient of determination (R2) and root mean square value (RMSE) were calculated on the back-transformed values of predicted water temperature for each fold and then averaged across folds. Last, we took the overall best model (see Results and discussion) and used this to calculate gauge-specific R2 and RMSE values. These allowed us to assess the predictive power of the best model for each site and explore any spatial patterns in model fit. We determined the adequacy of model predictions at each gauge by using the following criteria as recommended by Moriasi et al. (2015): very good (R2 > 0.8), good (0.70 ≤ R2 ≤ 0.80), satisfactory (0.5 < R2 < 0.70) and not satisfactory (R2 ≤ 0.50).
Results and discussion
Relative importance of air temperature and stream flow
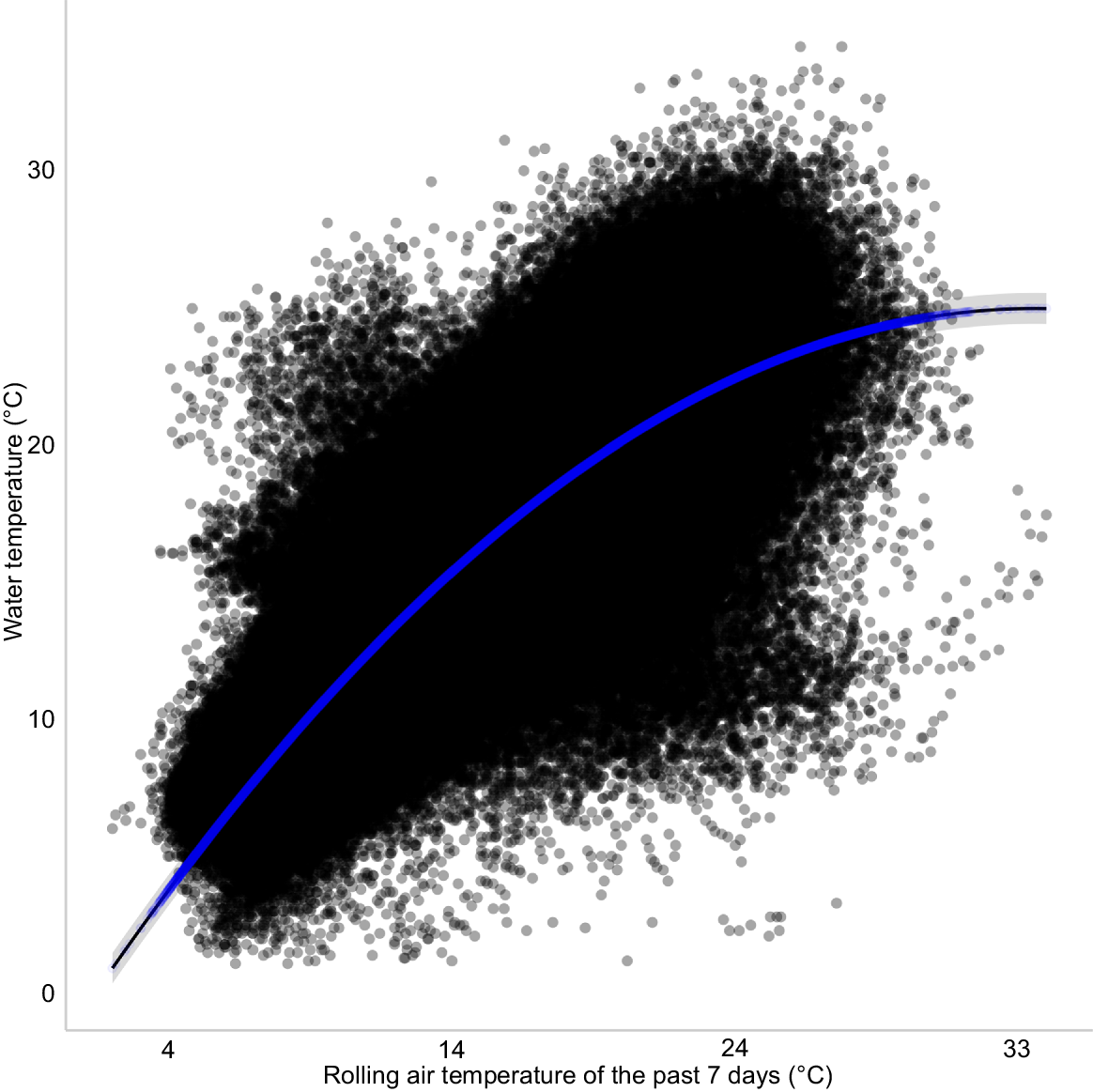
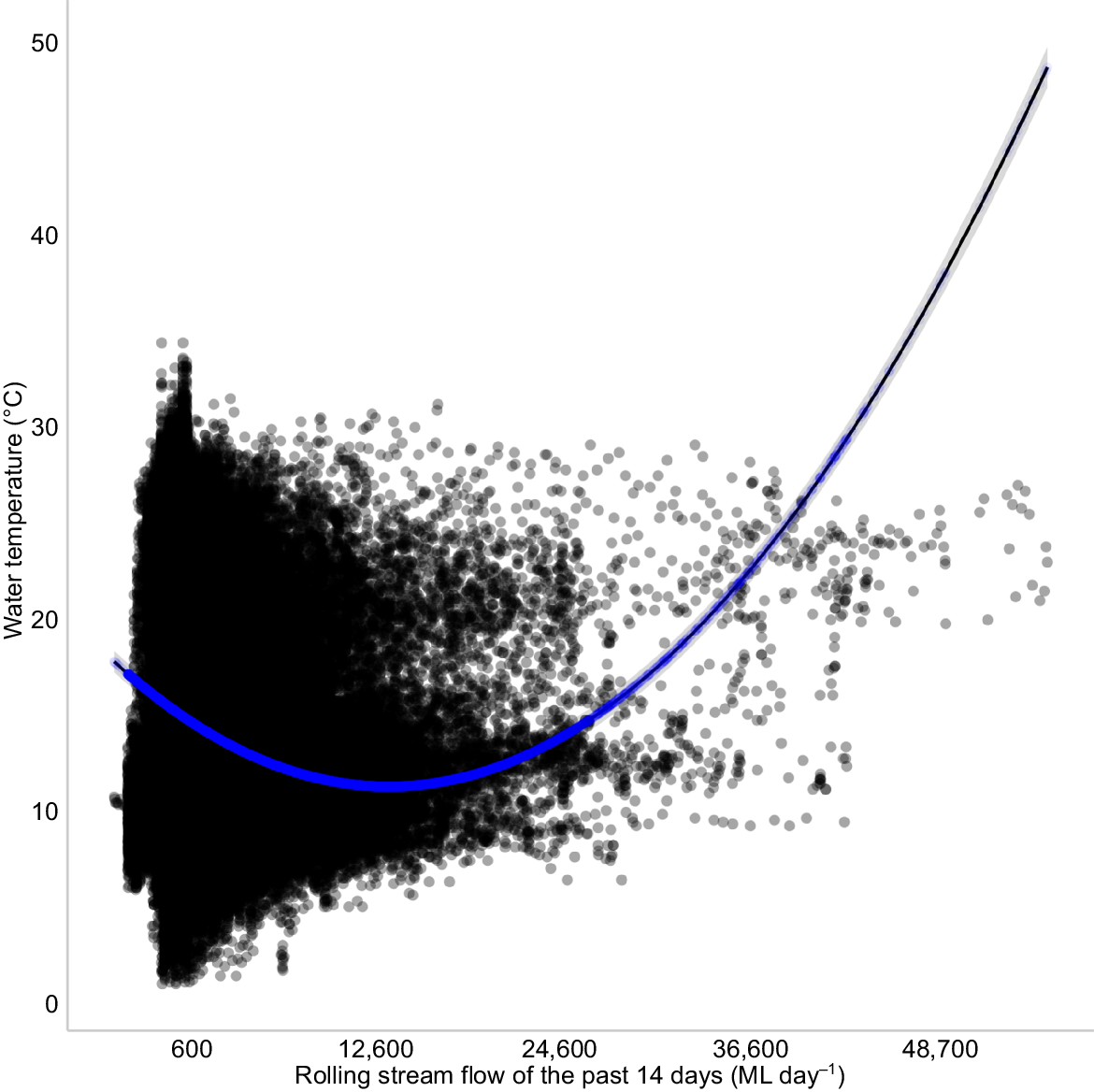
The inclusion of any air temperature variable and, to a lesser degree, any stream flow variable, improved the predictive performance of all models compared with the intercept-only null, which had a R2 = 0.02 and RMSE = 5.18 (Table 2). Models that included any air temperature variable performed better (R2 = 0.65–0.77, RMSE = 2.52–3.12) than did those that included any stream flow variable (R2 = 0.04–0.05, RMSE = 5.12–5.15). A quadratic effect of average air temperature over the past 7 days explained the most variation in daily water temperature observations and, consequently, had a much higher predictive power (R2 = 0.77, RMSE = 2.52) than did the best stream flow model that included linear and quadratic terms for average stream flow of the past 14 days (R2 = 0.05, RMSE = 5.12). Water temperature was positively and linearly related to rolling air temperature of the past 7 days until ~22.5°C, after which the relationship began to level off (Fig. 2). By contrast, water temperature was best predicted by a negative quadratic relationship to rolling stream flow of the past 14 days, reaching minimal water temperatures at a stream flow of ~12,700 mL day−1, then increasing thereafter (Fig. 3).
| Model | d.f. | LogLik | R2 | RMSE | |
|---|---|---|---|---|---|
| Null model | 4 | −674,860.36 | 0.02 | 5.18 | |
| Air temperature predictors | |||||
| meanDailyAir + meanDailyAir2 | 6 | −274,958.85 | 0.65 | 3.12 | |
| lagAir_1 + lagAir_12 | 6 | −216,504.80 | 0.69 | 2.93 | |
| lagAir_2 + lagAir_22 | 6 | −251,588.41 | 0.66 | 3.06 | |
| rollAir_2 + rollAir_22 | 6 | −175,094.83 | 0.71 | 2.80 | |
| rollAir_7 + rollAir_72 | 6 | −630,46.51 | 0.77 | 2.52 | |
| rollAir_14 + rollAir_142 | 6 | −112,719.91 | 0.75 | 2.65 | |
| Stream flow predictors | |||||
| meanDailyFlow + meanDailyFlow2 | 6 | −668,035.04 | 0.04 | 5.15 | |
| lagFlow_1 + lagFlow_12 | 6 | −668,317.14 | 0.04 | 5.15 | |
| lagFlow_2 + lagFlow_22 | 6 | −668,803.34 | 0.04 | 5.15 | |
| rollFlow_2 + rollFlow_22 | 6 | −667,212.54 | 0.04 | 5.14 | |
| rollFlow_7 + rollFlow_72 | 6 | −665,220.38 | 0.05 | 5.13 | |
| rollFlow_14 + rollFlow_142 | 6 | −665,023.28 | 0.05 | 5.12 | |
All models had the same random effects structure that allowed for water temperature observations to be nested within sites, which themselves were nested within drainage basins (1|drainage basin/gauge). Shown are model degrees of freedom (d.f.), log likelihood (logLik), coefficient of determination (R2) and root mean square value (RMSE). Models with the highest R2 value and the lowest RMSE value in their respective suite are in bold.
Predicted daily water temperature (±95% CI) as a function of rolled air temperature of past 7 days. Black points represent observed measurements of water temperature.
Predicted daily water temperature (±95% CI) as a function of rolling stream flow of the past 14 days. Black points represent observed measurements of water temperature.
Previously, air temperatures lagged from 0 to 8 days were found to best predict stream water temperatures (Stefan and Preud’homme 1993). We interpret our model selection of average air temperature of the past 7 days, which sits within this range, as a reflection of the low thermal inertia of water relative to air, which results in water requiring much more energy (in this case heating time) to increase in temperature (Erickson and Stefan 2000). The optimal duration to adequately capture the effects of thermal inertia has been shown to vary depending on the size of the waterbody (Stefan and Preud’homme 1993). Our study sites include a range of waterbody sizes, and the average air temperature of the past 7 days may thus serve as the best universal integration period. Rosencranz et al. (2021) also found that an average air temperature of the past 7 days was important in predicting water temperature across sites in southern Ontario, Canada. Their best-performing model structure included five parameters, one for each cumulative lagged air temperature of Days 1–5 prior to the target day. We chose not to explore this type of model structure because the different lagged parameters would be highly co-linear and thus affect the interpretation of our model.
Our stream flow model determined a negative quadratic relationship between stream flow and water temperature, which could be driven by the effect of stream flow across differently sized watercourses. Increasing stream flows within small watercourses could cause fast flows where there is little time to equilibrate with the surrounding atmosphere, and thus water temperatures deviate from air temperature (Smith and Lavis 1975). Once a minimum volume of stream flow is reached, the watercourse is likely to be larger and hence increasing water flow results in increased mixing and this increases the rate of heat transfer between air temperature and water temperature (Booker and Whitehead 2022). The best-performing stream flow model integrated conditions over 14 days. We believe that the longer stream flow duration may help capture temporal variation in stream morphology, because increasing stream flow results in larger stream channel width and depth (Leopold and Maddock 1953), which then affects heat transfer (Caissie et al. 2007). These specific aspects of stream morphology were otherwise not represented in our model because of the lack of available data. However, across all models, the predictive power of stream flow was much lower than that of air temperature. Additionally, the stream flow model predicted water temperatures outside observed water temperature ranges and, overall, had poor predictive performance. For both air temperature and stream flow variables, averaged durations for air temperature and stream flow were preferred over lagged predictors, which may reflect the smoothing out of empirical errors in environmental data (Rosencranz et al. 2021), as well as allowing a longer duration of environmental conditions to inform model predictions.
Catchment characteristics
The inclusion of catchment characteristics, in particular elevation, improved the predictive power of our water temperature models (Table 3). The best catchment characteristics model included a two-way interaction between average air temperature of the past 7 days and elevation (Table 3). Water temperature was positively related to air temperature of the past 7 days, with this relationship being marginally stronger at lower elevations (Fig. 4). Both elevation and catchment improved the predictive power of stream flow models, with elevation being slightly better (Table 3). However, all stream flow models had much poorer performance than did air temperature models.
| Model | d.f. | LogLik | R2 | RMSE | |
|---|---|---|---|---|---|
| Air temperature models | |||||
| rollAir_7 + rollAir_72 | 6 | −63,046.51 | 0.77 | 2.52 | |
| rollAir_7 + rollAir_72 + Elevation + Elevation:rollAir_7 | 8 | −62,366.21 | 0.81 | 2.30 | |
| rollAir_7 + rollAir_72 + Upstream Catchment Area | 7 | −63,021.53 | 0.78 | 2.47 | |
| Stream flow models | |||||
| rollFlow_14 + rollFlow_142 | 6 | 665,023.28 | 0.05 | 5.12 | |
| rollFlow_14 + rollFlow_142 + Elevation + Elevation:rollFlow_14 | 8 | 664,764.54 | 0.08 | 5.00 | |
| rollFlow_14 + rollFlow_142 + Upstream Catchment Area + Upstream Catchment Area:rollFlow_14 | 8 | 664,899.62 | 0.06 | 5.09 | |
All models had the same random effects structure that allowed for water temperature observations to be nested within sites, which themselves were nested within drainage basins (1|drainage basin/gauge). Shown are model degrees of freedom (d.f.), log likelihood (logLik), coefficient of determination (R2) and root mean square value (RMSE). Models with the highest R2 value and the lowest RMSE value in their suite are in bold.
Predicted daily water temperature (±95% CI) as a function of rolling air temperature and elevation.
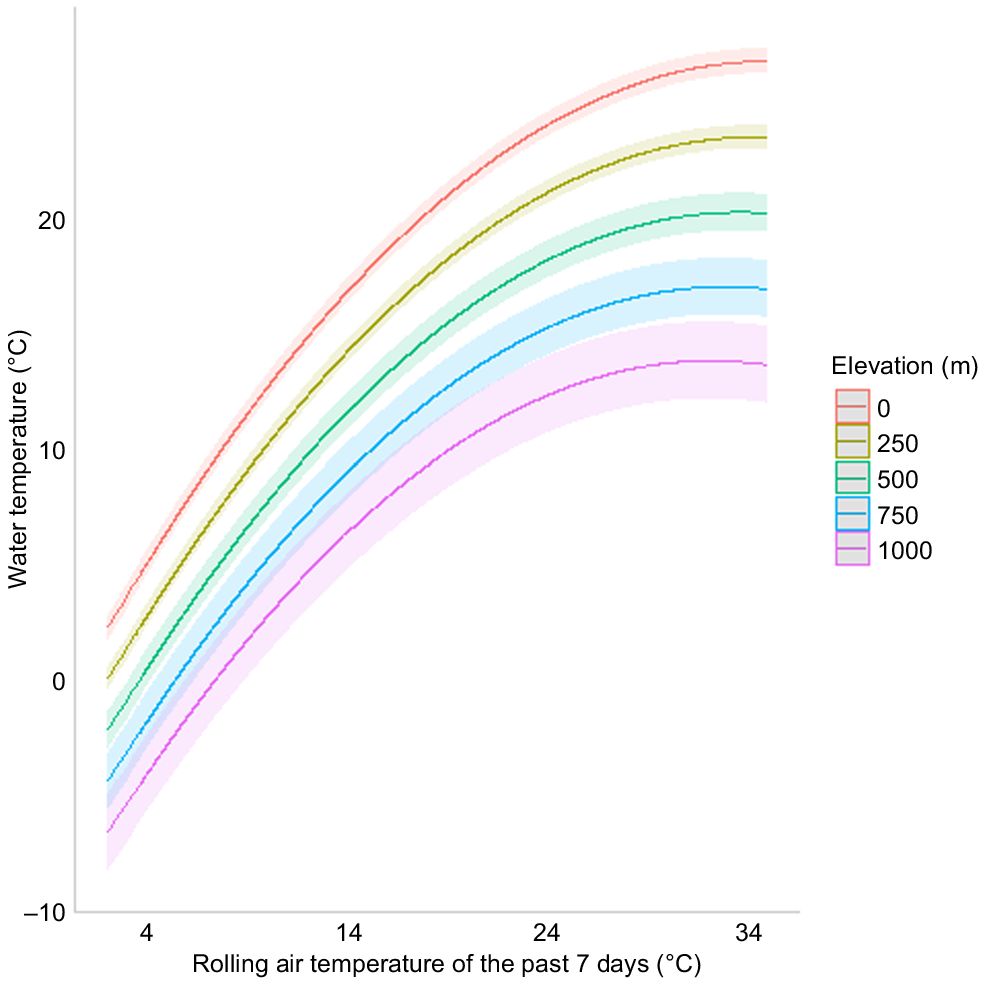
Water temperatures in high-elevation streams are predicted to increase under future climate change conditions, with the potential to affect alpine ecosystems (Shackleton et al. 2024). Our model identified a decreased sensitivity of water temperature to air temperature at higher elevations, which could be caused by reduced exposure to air temperature as watercourses are closer to their sources and thus have not travelled far through the system (Gu et al. 1998). However, the direction of the elevation and air temperature interaction, also called elevation-dependent warming or EDW, can vary depending on whether mechanistic or predictive models are used (Isaak and Luce 2023). Mechanistic models may show increased EDW because of overly prescriptive heat energy balance calculations (Luce et al. 2014; Isaak and Luce 2023), whereas most statistical models, including our own model, may show decreased EDW because they neglect the influence of groundwater, which can have a larger impact on water temperature at high elevations (Kurylyk et al. 2015; Leach and Moore 2019). Furthermore, groundwater may potentially increase thermal stability to high elevations and streams because it is less affected by seasonal or short-term fluctuations in air temperature (Agudelo-Vera et al. 2020). The inclusion of groundwater into statistical models would be a further improvement; however, it is difficult to determine the role of groundwater because of the lack of estimates of inflow rates and its temperature, especially at high-elevation areas (Somers and McKenzie 2020). Last, only 5% of gauges used to train our model occurred at elevations greater than 500 m, with only one gauge being located at an elevation greater than 1000 m. It is possible that this restricted extent of observations could have limited the capacity of our model to accurately capture water temperature dynamics at higher elevations. We undertook 10-fold cross-validation to account for data variability, but it could be that these scarce high-elevation sites were not well represented. Further work could explore the applicability of our model in regions with a relatively greater prevalence of higher-elevation data.
Elevation and upstream catchment area are correlated geographic properties (r = −0.311, d.f. = 148, P < 0.001), in that higher elevation water courses generally have lower upstream catchment areas than do those found at lower elevations (Fig. S18). That said, elevation and upstream catchment area capture nuanced aspects of the landscape. Elevation has been retained over upstream catchment area in other studies (e.g. Struthers et al. 2024), presumably because it serves as a universal surrogate for precipitation and cool air temperatures (sensuSiegel and Volk 2019). Importantly, elevation also captures aspects of land use within our study area (De Rose et al. 2008). The expansion of agriculture and urban development has reduced riparian vegetation and is associated with increased river regulation. Both shading from riparian vegetation (Garner et al. 2014) and river regulation (Erickson and Stefan 2000; Moore 2006) affect water temperature. In Victoria, the majority of land-use change away from native vegetation has occurred at lower elevations (De Rose et al. 2008). In contrast to elevation, upstream catchment size may be further removed from aspects of land use and more linked to stream size and discharge (Ver Hoef et al. 2006; Isaak et al. 2017). Indeed, average daily stream flow was correlated to upstream catchment size (r = 0.445, d.f. = 148, P < 0.001) but not to elevation (r = −0.082, d.f. = 148, P < 0.320) (Fig. S18) for our study region. These aspects of watercourse size and stream flow may already be adequately captured within stream flow predictors or may be of less importance relative to the aspects of land-use captured by elevation.
Predictive performance of combined air temperature and stream flow
The best-performing air temperature and stream flow model included a two-way interaction between these variables, as well as two-way interactions between air temperature and elevation, and stream flow and elevation (Table 4). However, this complex model did not perform better than did the simpler air temperature and elevation only model (Table 3), with both models having the same predictive power (R2 = 0.81, RMSE = 2.29). Thus, air temperature and elevation are adequate in predicting water temperature across a large geographic area and coefficients for the air temperature and elevation model are presented in Table 5. Note, these coefficients can be used to return only the conditional prediction of expected water temperature (i.e. effect of air temperature and elevation at an average site within our model domain), rather than marginal predictions (i.e. average effect of predictors across all sites in our domain) or unit-level predictions (e.g. predicted water temperature at a specific gauge). We provide predicted daily water temperature by using this model for 670 gauges across our study region from 7 January 1970 to 31 December 2022 (appendix 1, see https://github.com/trishfishkoh/predict_watertemp).
| Model | d.f. | LogLik | R2 | RMSE | |
|---|---|---|---|---|---|
| rollAir_7 + rollAir_72+ rollFlow_14 + rollFlow_142 + rollAir_7:rollFlow_14 | 9 | 61,643.15 | 0.77 | 2.52 | |
| rollAir_7 + rollAir_72 + rollFlow_14 + rollFlow_142 + rollAir_7:rollFlow_14 + Elevation + Elevation:rollAir_7 + Elevation:rollFlow_14 + Elevation:rollAir_7:rollFlow_14 | 13 | 60,528.14 | 0.81 | 2.30 | |
| rollAir_7 + rollAir_72 + rollFlow_14 + rollAir_7:rollFlow_14 + UpstreamCatchmentArea + UpstreamCatchmentArea:rollAir_7 + UpstreamCatchmentArea:rollFlow_14 + UpstreamCatchmentArea:rollAir_7:rollFlow_14 | 12 | 60,219.68 | 0.78 | 2.47 |
All models had the same random effects structure that allowed for water temperature observations to be nested within sites, which themselves were nested within drainage basins (1|drainage basin/gauge). Shown are model degrees of freedom (d.f.), log likelihood (logLik), coefficient of determination (R2) and root mean square value (RMSE). Models with the highest R2 value and the lowest RMSE value in their suite are in bold.
| Term | Estimate | s.e. | t-value | |
|---|---|---|---|---|
| Intercept | 3.865 | 0.283 | 136.477 | |
| Fixed effects | ||||
| elevationScaled | −0.177 | 0.015 | −11.831 | |
| rollAir_7Scaled | 0.619 | 3.670 × 10−4 | 1686.919 | |
| rollAir_7Scaled2 | −0.106 | 3.123 × 10−4 | −338.415 | |
| elevationScaled:rollAir_7Scaled | 0.017 | 4.687 × 10-4 | 35.511 | |
| Random effects | s.d. | Variance | ||
|---|---|---|---|---|
| gauge:drainage basin | 0.144 | 0.021 | ||
| drainage basin | 0.122 | 0.015 | ||
| Residual | 0.265 | 0.070 | ||
Other studies have identified stream flow as an important predictor of water temperature (Dugdale et al. 2017; Booker and Whitehead 2022). The effect of stream flow on water temperature may be dependent on the size of the watercourse or seasonality (Van Vliet et al. 2011). The relative importance of stream flow may vary through time, with the timing and magnitude of flows having a stronger effect on maximum water temperature in the warmest months (Van Vliet et al. 2011; Asarian et al. 2023). Our water temperature predictions may, therefore, be improved with a more complex model that allows for seasonal weighting of stream flow impacts. That said, our stream flow only models still performed poorly compared with air temperature only models, which suggests that hydrology is of less importance than is atmospheric temperature in determining water temperature in our study region.
Spatial and temporal performance of the best model
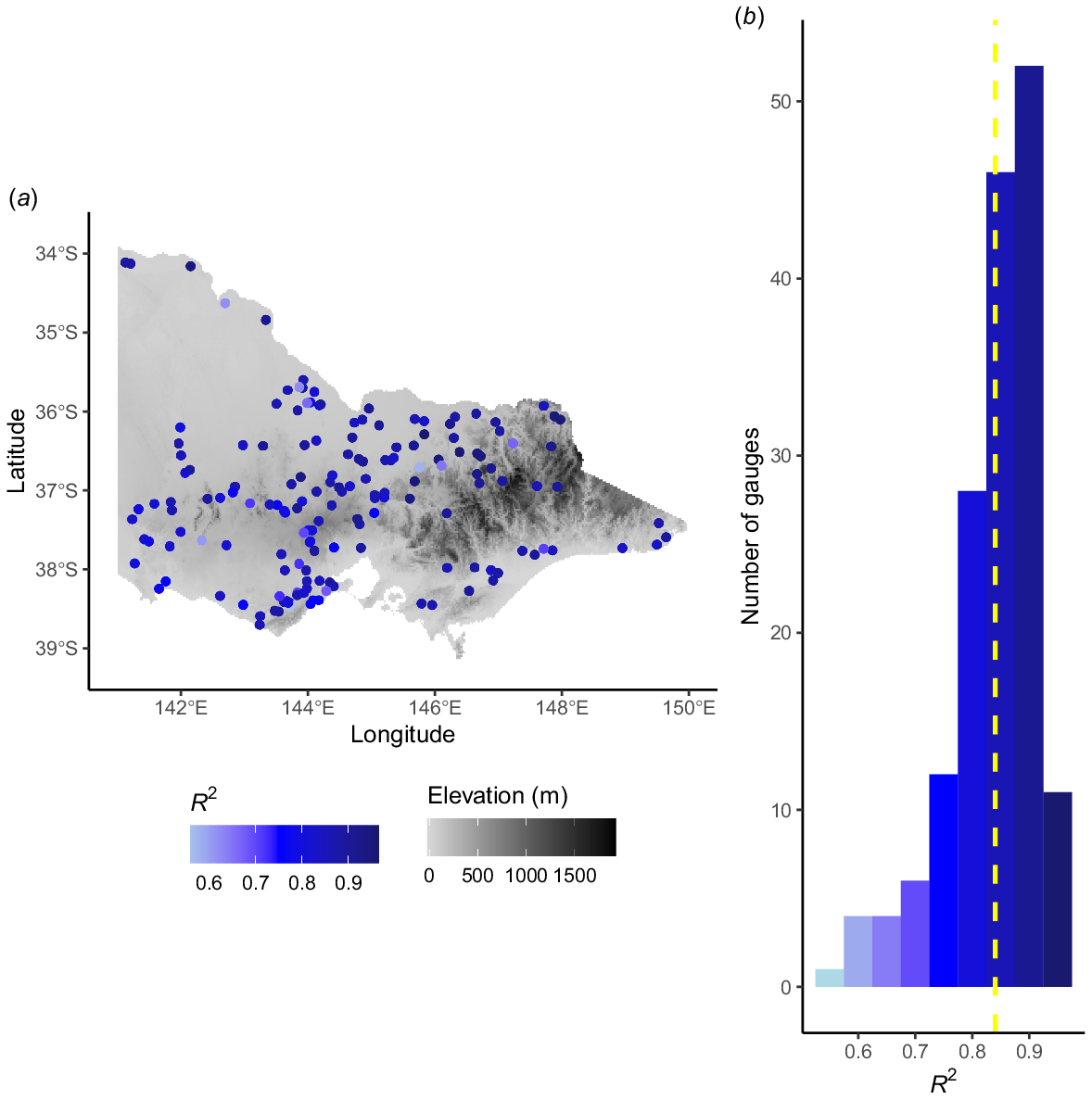
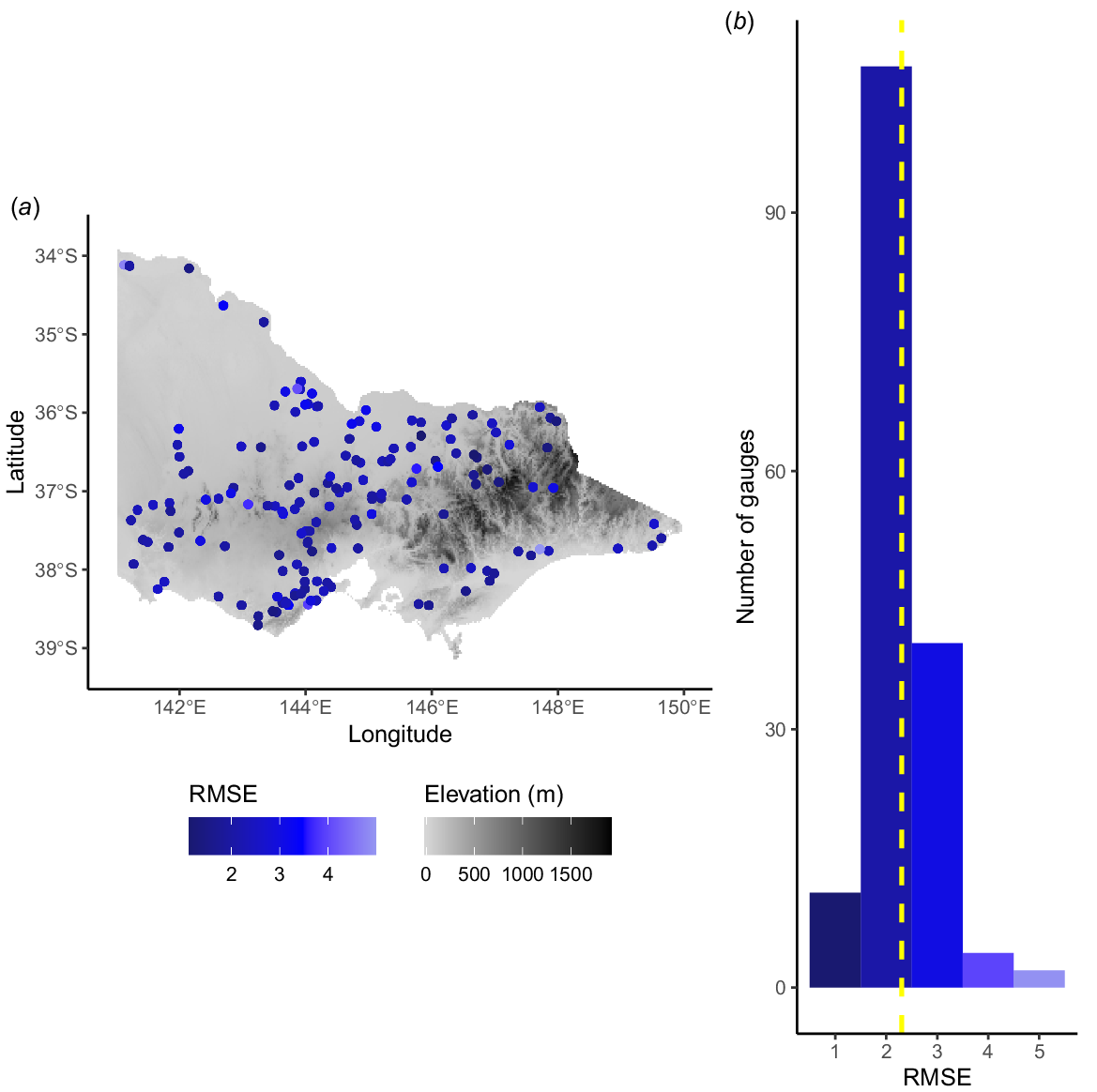
Our air temperature and elevation model had a generally very good performance across the spatial extent of our study, and we detected no obvious geographic clustering of poor-performing sites that would indicate systematic model bias (Fig. 5a, 6a). The average predictive performance of the model across sites was very good, with a mean R2 of 0.84 and a mean RMSE of 2.30°C (Fig. 5b, 6b). Importantly, all gauges had a satisfactory score with all R2 values above 0.5 and RMSE values ranging from 1.12 to 4.99°C. Here, we provide a discussion of good and poor model predictions by using several examples from the Ovens River catchment and from two particularly low-performing gauges. These examples show that our model accurately captures seasonal variation in temperature, but does not predict more rarely occurring extreme high temperatures as well.
(a) Plot of R2 values of best fit model, including air temperature and elevation. Background shading indicates elevation (m). (b) Histogram of R2 values. Yellow dotted line indicates the average R2 values across sites.
(a) Plot of RMSE values of best fit model, including air temperature and elevation. Background shading on map indicates elevation (m). (b) Histogram of RMSE values. Yellow dotted line indicates the average RMSE values across sites.
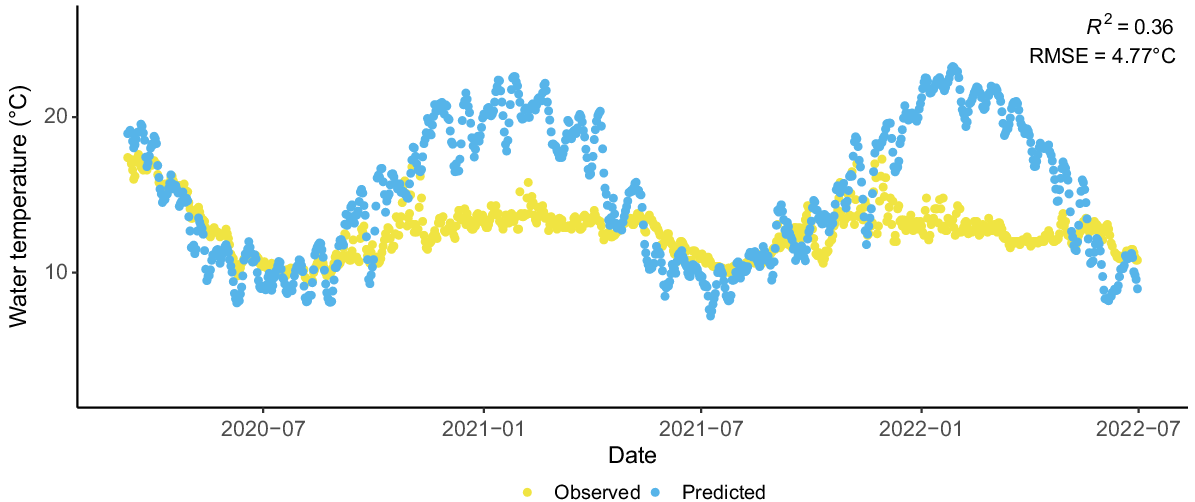
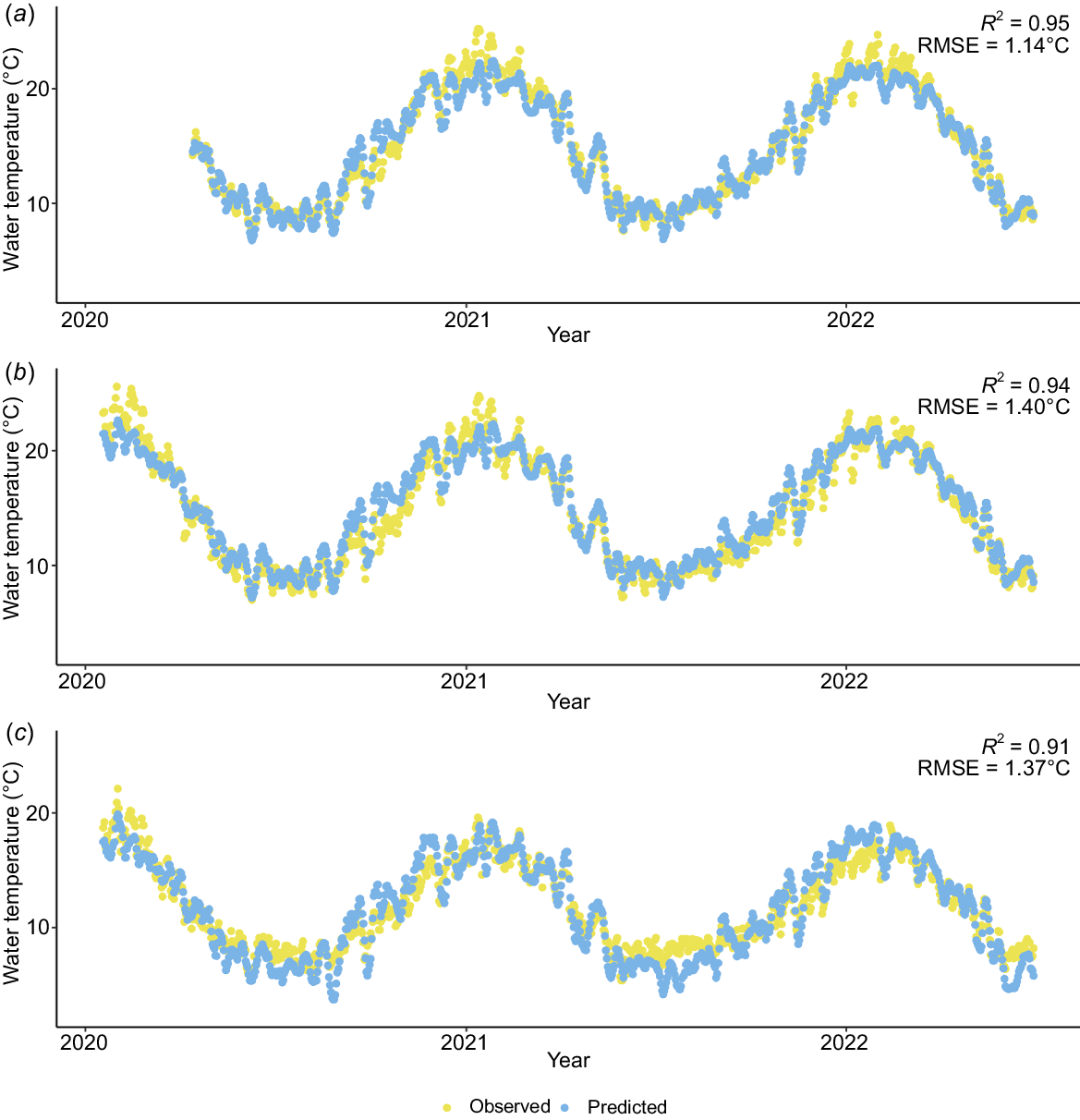
Water temperature estimates for the Ovens River at Rocky Point (Gauge 403230) (Fig. 7a) had a R2 of 0.95 and RMSE value of 1.14°C. Here, the predicted values accurately captured the temporal dynamics of daily water temperature, although there was some underestimation of water temperature when actual water temperatures were above 22°C (Fig. S19). Further upstream on the same river, Ovens River at Myrtleford (Gauge 403210) had equally high performance with a R2 of 0.94 and RMSE value of 1.40°C, but again there was an underestimation of warmer water temperatures (Fig. 7b). The highest elevation gauge on the Ovens River (at Harrietville, Gauge 403244), has a R2 of 0.91 and RMSE value of 1.37°C (Fig. 7c). This gauge did not exhibit the same underestimation of warm water temperatures experienced by gauges further downstream, presumably because temperature rarely surpassed 20°C. Instead, predicted water temperature was underestimated at lower actual temperatures. Despite some minor differences in fit, Fig. 7 indicates that our model skilfully captures observed water temperature dynamics. This suggests that our predictions will provide accurate data to studies that rely on the aggregation of water temperature over weekly, monthly or seasonal time periods, as is common in ecological studies (Morrongiello et al. 2014; Tonkin et al. 2019).
Plotted predicted and observed values for three gauges along the Ovens River: (a) Ovens River at Rocky Point (Gauge 403230); (b) Ovens River at Myrtleford (Gauge 403210); and (c) Ovens River at Harrietville (Gauge 403244).
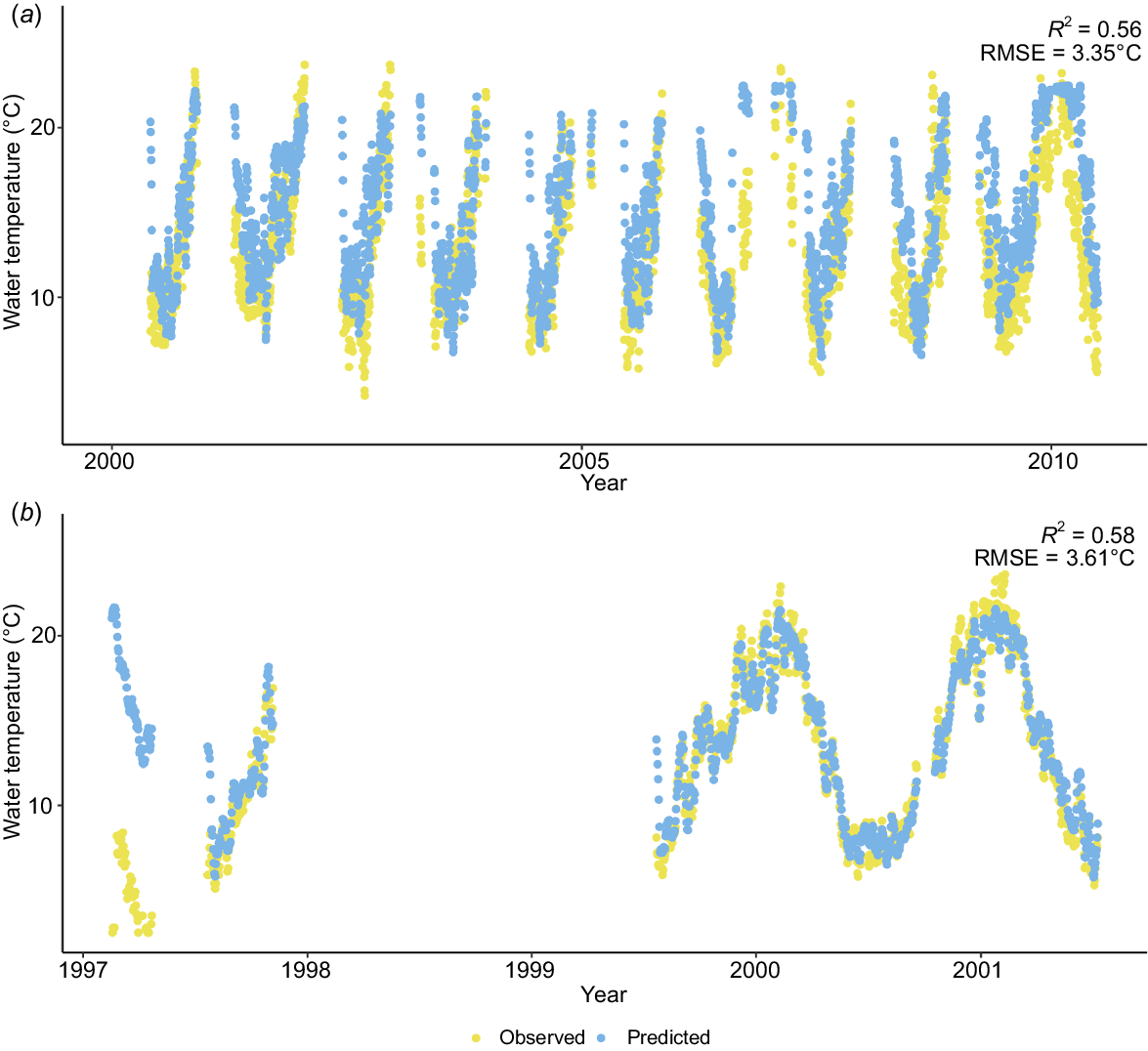
Two gauges, 233250 (Agroforestry Site at Racecourse Paddock Gerangamete) (Fig. 8a) and 405294 (Honeysuckle Creek at Violet Town) (Fig. 8b), had overall poor predictive performance (R2 < 0.58, RMSE > 3.35°C). The exact cause of predicted water temperature discrepancies is unknown, but we note that the observational record at Gauge 233250 had multiple gaps, which could be indicative of potential instrumental errors, whereas the instrument at Gauge 405294 recorded summer temperatures in 1997 that were implausibly cooler than were winter temperatures in other years. Thus, our model could be used to identify and infill erroneous water temperature records (see Fig. S20 for an example). Other generally poorly performing sites recorded extreme water temperatures with highly frequent fluctuations. These sites were often in agricultural areas, with presumably reduced riparian vegetation cover. We hypothesise that these gauges were exposed to higher local solar radiation, and coupled with modified and low stream flow, manifested in extreme water temperature fluctuations that exceeded 22.5°C or dropped to below 6°C. Extreme water temperatures were also observed at well-performing sites and model predictions deviated from observed water temperatures when observations exceeded these water temperature limits. Previous studies have shown that the linear relationship between air temperature and water temperature begins to desynchronise when temperatures fall below 0°C or rise above 20°C (Mohseni and Stefan 1999; Webb et al. 2003). However, observations in our data set beyond these extreme temperatures are relatively infrequent (Fig. S21) and, within these limits, our model performs well.
Plotted predicted and observed values for two poorly performing gauges: (a) Agroforestry Site at Racecourse Paddock Gerangamete (Gauge 233250); and (b) Honeysuckle Creek at Violet Town (Gauge 405294).
There are several impoundments in our study area that are known sources of cold-water pollution to downstream river reaches (Ryan et al. 2001). We therefore explicitly excluded gauges directly downstream of dams from model development because the water temperature profile of these sites is not reflective of broader patterns and characteristics of natural and less regulated streams and rivers. However, a comparison of predicted v. observed water temperature at these gauges provides us an opportunity to explore the spatial extent of cold-water pollution impacts.
Here, we demonstrate how the introduction of cold-water pollution from Lake Eildon affects water temperature by using four gauges located on the Goulburn River. Our model had high predictive capacity at the gauged site upstream of Lake Eildon on the Jamieson River (Table 6). The immediate impact of cold-water pollution is clearly evident at the gauged site 4 km downstream of Lake Eildon where our model poorly predicted water temperature (Fig. 9). We then observed a gradual improvement in model fit at gauges progressively further downstream of Lake Eildon, indicating that water temperatures are returning to what would be expected, given the site’s elevation and ambient air temperature (Table 6). Our findings are corroborated by previous work, showing that cold-water pollution from Lake Eildon extends as far as Molesworth, ~59 km downstream (Sinclair Knight Merz 2005).
| Location (gauge number) | Distance from dam wall | R2 | RMSE (°C) | |
|---|---|---|---|---|
| Jamieson at Gerrang Bridge (Gauge 405218) A | −43 km | 0.91 | 1.7 | |
| Goulburn River at Eildon (Gauge 405203) B | 4 km | 0.36 | 4.76 | |
| Goulburn River at Trawool (Gauge 405201) | 113 km | 0.81 | 1.98 | |
| Goulburn River at Murchison (Gauge 405200) | 214 km | 0.87 | 2.28 |
Applications and transferability
Our model provides an objective and reproducible method for infilling spatial and temporal gaps in water temperature datasets. The development of more complete, or even new, water temperature time series has obvious applicability for those conducting ecological studies that focus on relative or broad-scale changes in environmental conditions. Accurate, or even existing, water temperature records can be difficult to attain for many temporal periods or over large geographic locations. As a result, many ecological studies resort to using air temperature as a proxy in the absence of water temperature measurements (e.g. Morrongiello et al. 2011; Bond et al. 2011). Our model can be used to provide relative water temperature estimates that are more biologically relevant to freshwater fish. However, owing to our average RMSE of 2.30°C, our model may not be suitable for eco-physiological studies where more accurate measurements may be required (e.g. Stoffels et al. 2016).
While we focus our study on south-eastern Australia, we believe that this modelling approach could be transferred to other regions with a similar hydrology and climate. This could include areas predominantly featuring temperate warm summers such as the UK, parts of Europe and southern parts of South America (Peel et al. 2007). As always, users should train our model (hosted on Github at https://github.com/trishfishkoh/predict_watertemp) on their own available water temperature and air temperature estimates to calibrate parameters and ensure predictions are sensible. Conditional and marginal predictions can readily be made to new gauges within the environmental domain of our model by using R packages such as ggeffects (see https://cran.r-project.org/package=ggeffects) or marginaleffects (see https://cran.r-project.org/package=marginaleffects), which allow, where necessary, to average, marginalise or integrate across existing random effects. Additionally, because our model has not been tested and trained in areas with significant snowmelt, we caution its use in areas where there is significant snow, ice and glacial melt.
Conclusions
We successfully developed a model to predict water temperature with very good performance by using readily available environmental predictors. We found that average air temperature over the preceding 7 days explained the most variation in water temperature across all parameter combinations. The addition of stream flow provided little additional benefit to model fit or predictive capacity. The inclusion of site elevation alongside air temperature improved model predictions more than including upstream catchment area. Our approach demonstrated that water temperature can be readily modelled using elevation and air temperature across large spatial and temporal scales. Our work has obvious benefits for the estimation of water temperature time series far beyond restrictions imposed by the current monitoring network. This is important given that water temperature is a key driver of biological and ecological processes in freshwater environments.
Data availability
Supplementary figures are available as accompanying supplementary material. Appendix 1 and additional code have been made available at https://github.com/trishfishkoh/predict_watertemp.
Declaration of funding
This research was supported by The University of Melbourne’s Research Computing Services and the Petascale Campus Initiative. This research did not receive any specific funding.
Acknowledgements
P. Y. Koh thanks Dr Tianxiao Hao for assisting with high-performance computing systems. The authors thank the two anonymous reviewers who provided well-considered and constructive comments that helped refined this article.
References
Abdi R, Endreny T (2019) A river temperature model to assist managers in identifying thermal pollution causes and solutions. Water 11(5), 1060.
| Crossref | Google Scholar |
Agudelo-Vera C, Avvedimento S, Boxall J, Creaco E, De Kater H, Di Nardo A, Djukic A, Douterelo I, Fish KE, Iglesias Rey PL, Jacimovic N, Jacobs HE, Kapelan Z, Martinez Solano J, Montoya Pachongo C, Piller O, Quintiliani C, Ručka J, Tuhovčák L, Blokker M (2020) Drinking water temperature around the globe: understanding, policies, challenges and opportunities. Water 12(4), 1049.
| Crossref | Google Scholar |
Ahmadi-Nedushan B, St-Hilaire A, Ouarda TBMJ, Bilodeau L, Robichaud É, Thiémonge N, Bobée B (2007) Predicting river water temperatures using stochastic models: case study of the Moisie River (Québec, Canada). Hydrological Processes 21(1), 21-34.
| Crossref | Google Scholar |
Arismendi I, Johnson SL, Dunham JB, Haggerty R (2013) Descriptors of natural thermal regimes in streams and their responsiveness to change in the Pacific Northwest of North America. Freshwater Biology 58(5), 880-894.
| Crossref | Google Scholar |
Asarian JE, Robinson C, Genzoli L (2023) Modeling seasonal effects of river flow on water temperatures in an agriculturally dominated California River. Water Resources Research 59(3), e2022WR032915.
| Crossref | Google Scholar |
Bates D, Mächler M, Bolker B, Walker S (2015) Fitting linear mixed-effects models using lme4. Journal of Statistical Software 67(1), 1-48.
| Crossref | Google Scholar |
Benyahya L (2014) Workshop on the development & implementation of a water temperature monitoring network for Atlantic salmon (Salmo salar) rivers in eastern Canada held in Quebec City, Quebec, 22–23 January 2014: abstracts and proceedings. Fisheries and Oceans Canada, Science Branch, Diadromous Fish Section, Moncton, NB, Canada.
Benyahya L, Caissie D, St-Hilaire A, Ouarda TBMJ, Bobée B (2007) A review of statistical water temperature models. Canadian Water Resources Journal 32(3), 179-192.
| Crossref | Google Scholar |
Bond N, Thomson J, Reich P, Stein J (2011) Using species distribution models to infer potential climate change-induced range shifts of freshwater fish in south-eastern Australia. Marine and Freshwater Research 62(9), 1043-1061.
| Crossref | Google Scholar |
Booker DJ, Whitehead AL (2022) River water temperatures are higher during lower flows after accounting for meteorological variability. River Research and Applications 38, 3-22.
| Crossref | Google Scholar |
Broadmeadow S, Nisbet TR (2004) The effects of riparian forest management on the freshwater environment: a literature review of best management practice. Hydrology and Earth System Sciences 8(3), 286-305.
| Crossref | Google Scholar |
Buisson L, Blanc L, Grenouillet G (2008) Modelling stream fish species distribution in a river network: the relative effects of temperature versus physical factors. Ecology of Freshwater Fish 17(2), 244-257.
| Crossref | Google Scholar |
Bureau of Meteorology (2017) Climate classification maps. (BOM) Available at http://www.bom.gov.au/climate/maps/averages/climate-classification/?maptype=tmp_zones [Verified 1 May 2024]
Caissie D (2006) The thermal regime of rivers: a review. Freshwater Biology 51(8), 1389-1406.
| Crossref | Google Scholar |
Caissie D, Satish MG, El-Jabi N (2007) Predicting water temperatures using a deterministic model: application on Miramichi River catchments (New Brunswick, Canada). Journal of Hydrology 336(3–4), 303-315.
| Crossref | Google Scholar |
De Rose RC, Stewardson MJ, Harman C (2008) Downstream hydraulic geometry of rivers in Victoria, Australia. Geomorphology 99(1–4), 302-316.
| Crossref | Google Scholar |
Dugdale SJ, Hannah DM, Malcolm IA (2017) River temperature modelling: a review of process-based approaches and future directions. Earth-Science Reviews 175, 97-113.
| Crossref | Google Scholar |
Dugdale SJ, Kelleher CA, Malcolm IA, Caldwell S, Hannah DM (2019) Assessing the potential of drone-based thermal infrared imagery for quantifying river temperature heterogeneity. Hydrological Processes 33(7), 1152-1163.
| Crossref | Google Scholar |
Dunham J, Chandler G, Rieman B, Martin D (2005) Measuring stream temperature with digital data loggers: a user’s guide. General Technical Report RMRS-GTR-150, USDA Forest Service, Rocky Mountain Research Station, Fort Collins, CO, USA. 10.2737/RMRS-GTR-150
Erickson TR, Stefan HG (2000) Linear Air/water temperature correlations for streams during open water periods. Journal of Hydrologic Engineering 5(3), 317-321.
| Crossref | Google Scholar |
Finlayson BL, McMahon TA (1988) Australia v the world: a comparative analysis of streamflow characteristics. Available at https://api.semanticscholar.org/CorpusID:227657878
Garner G, Malcolm IA, Sadler JP, Hannah DM (2014) What causes cooling water temperature gradients in a forested stream reach? Hydrology and Earth System Sciences 18(2), 5361-5376.
| Crossref | Google Scholar |
Garner G, Malcolm IA, Sadler JP, Hannah DM (2017) The role of riparian vegetation density, channel orientation and water velocity in determining river temperature dynamics. Journal of Hydrology 553, 471-485.
| Crossref | Google Scholar |
Gatien P, Arsenault R, Martel J-L, St-Hilaire A (2023) Using the ERA5 and ERA5-Land reanalysis datasets for river water temperature modelling in a data-scarce region. Canadian Water Resources Journal/Revue Canadienne Des Ressources Hydriques 48(2), 93-110.
| Crossref | Google Scholar |
Gu R, Montgomery S, Austin TA (1998) Quantifying the effects of stream discharge on summer river temperature. Hydrological Sciences Journal 43(6), 885-904.
| Crossref | Google Scholar |
Hauser S, Grams CM, Reeder MJ, McGregor S, Fink AH, Quinting JF (2020) A weather system perspective on winter–spring rainfall variability in southeastern Australia during El Niño. Quarterly Journal of the Royal Meteorological Society 146(731), 2614-2633.
| Crossref | Google Scholar |
Hébert C, Caissie D, Satish MG, El-Jabi N (2015) Predicting hourly stream temperatures using the equilibrium temperature model. Journal of Water Resource and Protection 07(4), 322-338.
| Crossref | Google Scholar |
Hersbach H, Bell B, Berrisford P, Biavati G, Horányi A, Muñoz Sabater J, Nicolas J, Peubey C, Radu R, Rozum I, Schepers D, Simmons A, Soci C, Dee D, Thépaut J-N (2023) ERA5 hourly data on pressure levels from 1940 to present. (Climate Data Store) [Dataset] doi:10.24381/CDS.BD0915C6
Hollister JW, Robitaille AL, Beck MW, Johnson JM, Shah T, Nowosad J (2023) Jhollist/elevatr: CRAN Release v0.99.0. Zenodo 2023, v0.99.0. [Program data, published 11 September 2023].
| Crossref | Google Scholar |
Isaak DJ, Horan DL (2011) An evaluation of underwater epoxies to permanently install temperature sensors in mountain streams. North American Journal of Fisheries Management 31(1), 134-137.
| Crossref | Google Scholar |
Isaak DJ, Luce CH (2023) Elevation-dependent warming of streams in mountainous regions: implications for temperature modeling and headwater climate refugia. Canadian Water Resources Journal/Revue Canadienne Des Ressources Hydriques 48(2), 167-188.
| Crossref | Google Scholar |
Isaak DJ, Wenger SJ, Peterson EE, Ver Hoef JM, Nagel DE, Luce CH, Hostetler SW, Dunham JB, Roper BB, Wollrab SP, Chandler GL, Horan DL, Parkes-Payne S (2017) The NorWeST summer stream temperature model and scenarios for the Western US: a crowd-sourced database and new geospatial tools foster a user community and predict broad climate warming of rivers and streams. Water Resources Research 53(11), 9181-9205.
| Crossref | Google Scholar |
Kennard MJ, Pusey BJ, Olden JD, Mackay SJ, Stein JL, Marsh N (2010) Classification of natural flow regimes in Australia to support environmental flow management. Freshwater Biology 55(1), 171-193.
| Crossref | Google Scholar |
Klinges DH, Duffy JP, Kearney MR, Maclean IMD (2022) mcera5: driving microclimate models with ERA5 global gridded climate data. Methods in Ecology and Evolution 13(7), 1402-1411.
| Crossref | Google Scholar |
Kurylyk BL, MacQuarrie KTB, Caissie D, McKenzie JM (2015) Shallow groundwater thermal sensitivity to climate change and land cover disturbances: derivation of analytical expressions and implications for stream temperature modeling. Hydrology and Earth System Sciences 19(5), 2469-2489.
| Crossref | Google Scholar |
Land Use Victoria (2023) VicMap. Available at https://www.land.vic.gov.au/maps-and-spatial/spatial-data/vicmap-catalogue
Leach JA, Moore RD (2019) Empirical stream thermal sensitivities may underestimate stream temperature response to climate warming. Water Resources Research 55(7), 5453-5467.
| Crossref | Google Scholar |
Leopold LB, Maddock T Jr (1953) The hydraulic geometry of stream channels and some physiographic implications. Professional Paper 252, US Department of the Interior, US Geological Survey, Washington, DC, USA. 10.3133/pp252
Letcher BH, Hocking DJ, O’Neil K, Whiteley AR, Nislow KH, O’Donnell MJ (2016) A hierarchical model of daily stream temperature using air–water temperature synchronization, autocorrelation, and time lags. PeerJ 4, e1727.
| Crossref | Google Scholar | PubMed |
Lisi PJ, Schindler DE, Cline TJ, Scheuerell MD, Walsh PB (2015) Watershed geomorphology and snowmelt control stream thermal sensitivity to air temperature. Geophysical Research Letters 42(9), 3380-3388.
| Crossref | Google Scholar |
Luce C, Staab B, Kramer M, Wenger S, Isaak D, McConnell C (2014) Sensitivity of summer stream temperatures to climate variability in the Pacific Northwest. Water Resources Research 50(4), 3428-3443.
| Crossref | Google Scholar |
Mohseni O, Stefan HG (1999) Stream temperature/air temperature relationship: a physical interpretation. Journal of Hydrology 218(3–4), 128-141.
| Crossref | Google Scholar |
Moore RD (Dan) (2006) Stream temperature patterns in British Columbia, Canada, based on routine spot measurements. Canadian Water Resources Journal 31(1), 41-56.
| Crossref | Google Scholar |
Moriasi DN, Gitau MW, Pai N, Daggupati P (2015) Hydrologic and water quality models: performance measures and evaluation criteria. Transactions of the ASABE 58(6), 1763-1785.
| Crossref | Google Scholar |
Morrongiello JR, Crook DA, King AJ, Ramsey DSL, Brown P (2011) Impacts of drought and predicted effects of climate change on fish growth in temperate Australian lakes. Global Change Biology 17(2), 745-755.
| Crossref | Google Scholar |
Morrongiello JR, Walsh CT, Gray CA, Stocks JR, Crook DA (2014) Environmental change drives long-term recruitment and growth variation in an estuarine fish. Global Change Biology 20(6), 1844-1860.
| Crossref | Google Scholar | PubMed |
Nicholls N, Drosdowsky W, Lavery B (1997) Australian rainfall variability and change. Weather 52(3), 66-72.
| Crossref | Google Scholar |
Ohlberger J (2013) Climate warming and ectotherm body size – from individual physiology to community ecology. Functional Ecology 27(4), 991-1001.
| Crossref | Google Scholar |
O’Carroll AG, Armstrong EM, Beggs HM, Bouali M, Casey KS, Corlett GK, Dash P, Donlon CJ, Gentemann CL, Høyer JL, Ignatov A, Kabobah K, Kachi M, Kurihara Y, Karagali I, Maturi E, Merchant CJ, Marullo S, Minnett PJ, Pennybacker M, Ramakrishnan B, Ramsankaran R, Santoleri R, Sunder S, Saux Picart S, Vázquez-Cuervo J, Wimmer W (2019) Observational needs of sea surface temperature. Frontiers in Marine Science 6, 420.
| Crossref | Google Scholar |
Peel MC, Finlayson BL, McMahon TA (2007) Updated world map of the Köppen–Geiger climate classification. Hydrology and Earth System Sciences 11(5), 1633-1644.
| Crossref | Google Scholar |
Riemer K, Anderson-Teixeira KJ, Smith FA, Harris DJ, Ernest SKM (2018) Body size shifts influence effects of increasing temperatures on ectotherm metabolism. Global Ecology and Biogeography 27(8), 958-967.
| Crossref | Google Scholar |
Rosencranz J, Cuddington K, Brook M, Koops MA, Drake DA (2021) Data-limited models to predict river temperatures for aquatic species at risk. Canadian Journal of Fisheries and Aquatic Sciences 78(9), 1268-1277.
| Crossref | Google Scholar |
Shackleton ME, Siebers AR, Suter PJ, Lines O, Holland A, Morgan JW, Silvester E (2024) Out of the frying pan into the fire: predicted warming in alpine streams suggests hidden consequences for aquatic ectotherms. Global Change Biology 30(6), e17364.
| Crossref | Google Scholar | PubMed |
Siegel JE, Volk CJ (2019) Accurate spatiotemporal predictions of daily stream temperature from statistical models accounting for interactions between climate and landscape. PeerJ 7, e7892.
| Crossref | Google Scholar | PubMed |
Smith K, Lavis ME (1975) Environmental influences on the temperature of a small upland stream. Oikos 26(2), 228-236.
| Crossref | Google Scholar |
Somers LD, McKenzie JM (2020) A review of groundwater in high mountain environments. WIREs Water 7(6), e1475.
| Crossref | Google Scholar |
Stefan HG, Preud’homme EB (1993) Stream temperature estimation from air temperature. JAWRA Journal of the American Water Resources Association 29(1), 27-45.
| Crossref | Google Scholar |
Stoffels RJ, Richardson AJ, Vogel MT, Coates SP, Müller WJ (2016) What do metabolic rates tell us about thermal niches? Mechanisms driving crayfish distributions along an altitudinal gradient. Oecologia 180, 45-54.
| Crossref | Google Scholar | PubMed |
Struthers DP, Gutowsky LFG, Lucas TCD, Mochnacz NJ, Carli CM, Taylor MK (2024) Statistical stream temperature modelling with SSN and INLA: an introduction for conservation practitioners. Canadian Journal of Fisheries and Aquatic Sciences 81(4), 417-432.
| Crossref | Google Scholar |
Te Wierik SA, Cammeraat ELH, Gupta J, Artzy-Randrup YA (2021) Reviewing the impact of land use and land-use change on moisture recycling and precipitation patterns. Water Resources Research 57(7), e2020WR029234.
| Crossref | Google Scholar |
Thornton PE, Shrestha R, Thornton M, Kao S-C, Wei Y, Wilson BE (2021) Gridded daily weather data for North America with comprehensive uncertainty quantification. Scientific Data 8, 190.
| Crossref | Google Scholar | PubMed |
Tonkin Z, Stuart I, Kitchingman A, Thiem JD, Zampatti B, Hackett G, Koster W, Koehn J, Morrongiello J, Mallen-Cooper M, Lyon J (2019) Hydrology and water temperature influence recruitment dynamics of the threatened silver perch Bidyanus bidyanus in a regulated lowland river. Marine and Freshwater Research 70(9), 1333-1344.
| Crossref | Google Scholar |
Torgersen CE, Faux RN, McIntosh BA, Poage NJ, Norton DJ (2001) Airborne thermal remote sensing for water temperature assessment in rivers and streams. Remote Sensing of Environment 76(3), 386-398.
| Crossref | Google Scholar |
Van Vliet MTH, Ludwig F, Zwolsman JJG, Weedon GP, Kabat P (2011) Global river temperatures and sensitivity to atmospheric warming and changes in river flow. Water Resources Research 47(2), W02544.
| Crossref | Google Scholar |
Ver Hoef JM, Peterson E, Theobald D (2006) Spatial statistical models that use flow and stream distance. Environmental and Ecological Statistics 13, 449-464.
| Crossref | Google Scholar |
Webb BW, Clack PD, Walling DE (2003) Water–air temperature relationships in a Devon river system and the role of flow. Hydrological Processes 17(15), 3069-3084.
| Crossref | Google Scholar |
Woods T, Freeman MC, Krause KP, Maloney KO (2023) Observed and projected functional reorganization of riverine fish assemblages from global change. Global Change Biology 29(13), 3759-3780.
| Crossref | Google Scholar | PubMed |
Zhao Q, Van Den Brink PJ, Xu C, Wang S, Clark AT, Karakoç C, Sugihara G, Widdicombe CE, Atkinson A, Matsuzaki S-IS, Shinohara R, He S, Wang YXG, De Laender F (2023) Relationships of temperature and biodiversity with stability of natural aquatic food webs. Nature Communications 14, 3507.
| Crossref | Google Scholar | PubMed |
Zhi W, Klingler C, Liu J, Li L (2023) Widespread deoxygenation in warming rivers. Nature Climate Change 13, 1105-1113.
| Crossref | Google Scholar |
Zhu S, Piotrowski AP (2020) River/stream water temperature forecasting using artificial intelligence models: a systematic review. Acta Geophysica 68, 1433-1442.
| Crossref | Google Scholar |