Wildfire risk assessment in Sichuan Province, China: hazard modeling approach considering different combinations of classification criteria and connection values of factor attributes
Weiting Yue A , Yunji Gao
A , Yunji Gao  A * , Yu Ma
A * , Yu Ma  A , Ziqun Ye
A , Ziqun Ye  A and Yuchun Zhang
A and Yuchun Zhang  A
A
A
Abstract
Current wildfire risk research has primarily focused on hazard assessment, lacking a comprehensive framework that integrates vulnerability and adaptive capacity. Moreover, the influence of different statistical connection methods and classification criteria of factor attributes on hazard assessment has been overlooked.
Taking Sichuan Province, China, as the study area, a comprehensive wildfire risk assessment model was constructed based on the hazard-vulnerability-adaptive capacity framework, with special focus on the effects of differences in connection methods and classification criteria of factor attributes on the modeling performance of wildfire hazard.
The impact of six connection methods integrated with logistic regression (LR) on wildfire hazard assessment was explored using wildfire samples/whole region as classification criteria. Vulnerability and adaptive capacity were analyzed using techniques for ranking preferences by similarity to ideal solutions (TOPSIS), coupled with combination weights and integrated with the optimal hazard model, resulting in an integrated risk assessment framework.
Significant differences between hazard assessment results based on different classification criteria and connection methods were found. The Point-IV-LR model, constructed using wildfire samples as classification criteria and utilizing information value (IV) coupled LR, performed the best. The risk assessment highlighted southwestern mountains as critical high-risk areas.
These findings provide targeted wildfire prevention strategies tailored to different risk levels in Sichuan Province.
Keywords: adaptive capacity, connection method, factor attribute classification, logistic regression, Sichuan Province, TOPSIS, vulnerability, wildfire risk assessment.
Introduction
Wildfires are highly destructive natural disasters, threatening ecosystems, socio-economic stability and public safety (Jaafari et al. 2018; Naderpour et al. 2019). In recent years, climate change and human activities have significantly increased the frequency, intensity and spatiotemporal complexity of wildfires globally (Sharma et al. 2022; Cunningham et al. 2024). As a wildfire-prone country, China experienced an average of 12,683 fires annually from 1950 to 2010, burning 6748 km2 per year (Su et al. 2015). In Sichuan Province, China, alone, reporting 4914 forest fires burning 53,608 ha from 2000 to 2014 (Xiong et al. 2020). These statistics underscore the urgency of conducting wildfire risk assessments to inform targeted fire management policies.
Risk is generally defined as the expected loss resulting from the interaction among hazard magnitude, vulnerability and adaptive capacity conditions (Hu et al. 2009). While existing studies have primarily concentrated on hazard assessment as a core component of wildfire risk research, this process aims to quantify hazard magnitude and spatial distribution through modeling approaches (Cao et al. 2017; Oliveira et al. 2021). Mainstream approaches to wildfire hazard assessment can be broadly categorized into qualitative analysis, physical simulation and data-driven methods (Yue et al. 2023). Qualitative methods, such as fuzzy logic and the analytic hierarchy process (AHP), rely on expert experience and subjective judgment to estimate the likelihood of wildfire occurrence (Erdin and Çağlar 2021; Nasiri et al. 2022). However, the assessment results may deviate from objective reality when subjective judgments are biased (Tavakkoli Piralilou et al. 2022). Physical simulation methods, grounded in fluid dynamics and heat transfer theory, utilize mathematical models to simulate and predict wildfire behavior (Guo et al. 2025). Nevertheless, the complexity of these models and the difficulty of data acquisition significantly limit their applicability over large geographic scales (Bui et al. 2017). Data-driven approaches primarily include statistical connection and machine learning (ML) methods. Although ML models often demonstrate higher predictive accuracy compared to statistical connection methods, they typically require large volumes of high-quality data. Furthermore, their complex architectures tend to compromise interpretability, generalization and stability. In contrast, connection methods such as frequency ratio (FR), information value (IV) and weights of evidence (WOE) have clearer logical structures, computational simplicity and stronger interpretability, which have led to their widespread application in wildfire hazard assessments across various regions (Hong et al. 2017; Nami et al. 2018; Tiwari et al. 2021; Sivrikaya and Küçük 2022). These methods can quantitatively describe the internal relationships between internal attributes of factors and wildfires, revealing the driving mechanisms behind wildfire hazards (Wang et al. 2024). However, connection methods generally assume independence among factors and fail to account for the relative importance of each factor. To address these limitations, many studies have attempted to integrate logistic regression (LR) models with connection methods to identify the importance of factors while enhancing the transparency of how different attribute intervals contribute to wildfire hazard. As a classic binary classification method with features of statistics and ML, the LR model does not rely on hyperparameter tuning, and offers robust performance and interpretability.
Despite significant progress in current wildfire risk research, there are still several gaps: (1) in hazard assessment, the differences in modeling accuracy and stability across various connection methods lack systematic comparative analysis, especially when coupled with LR models (Ke et al. 2023; Xing et al. 2023). Additionally, most studies adopt a single classification strategy, and have not thoroughly investigated the influence of different classification criteria of factor attributes – namely, classification based on wildfire sample distribution versus classification based on the whole region – on model outcomes; (2) from the overall framework, current wildfire risk research, supported by multi-source spatial information, remains predominantly focused on hazard assessment. Comprehensive risk assessment frameworks that integrate hazard, vulnerability and adaptive capacity are scarce. In contrast, similar composite indicator framework has been widely used in the risk assessment of other natural hazards such as floods, landslides and typhoons (Fedeski and Gwilliam 2007; Joyce et al. 2018; Nguyen et al. 2019). This indicates that wildfire risk research still requires further theoretical and methodological development.
In summary, this study constructed a comprehensive risk assessment framework based on f(hazard, vulnerability, adaptive capacity), using Sichuan Province as the study area. Among them, it focused on the impacts of six common statistical connection methods, when coupled with the LR model, on wildfire hazard assessment under the two distinct classification criteria of wildfire samples or the whole region. This study aims to provide a more comprehensive and theoretically grounded methodology for advancing wildfire risk assessment practices.
Study area and data collection
Study area
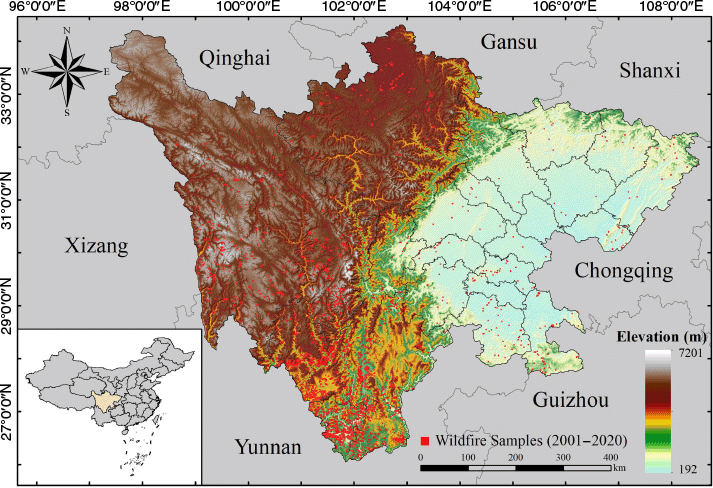
Sichuan Province, located in southwest China, features diverse landforms and significant elevation variations (Fig. 1). The eastern region is dominated by the relatively flat Sichuan Basin, while the western part consists of rugged mountainous terrain along the eastern edge of the Qinghai–Tibet Plateau (Ning et al. 2023). The climate in Sichuan is complex and varied, with stark variations in precipitation and temperature due to differences in terrain and elevation. These conditions support diverse vegetation types (Peng et al. 2019). With an overall vegetation cover of 85.6% and a forest coverage rate of 40.26%, Sichuan plays a crucial role in the national ecological landscape. However, its abundant vegetation also presents significant challenges for wildfire emergency response and management.
Data collection
The MODerate Resolution Imaging Spectroradiometer (MODIS) fire dataset was utilized as the primary source of wildfire samples. Provided by the Fire Information for Resource Management System (FIRMS) of NASA (https://firms.modaps.eosdis.nasa.gov/usfs/map/), this dataset has monitored fire points daily since 2000 via sensors onboard the Terra and Aqua satellites, with a spatial resolution of 1 km and four observations per day, effectively capturing wildfire dynamics (Li et al. 2018). The dataset includes observation coordinates, acquisition time, fire radiative power (FRP) and confidence levels, offering comprehensive support for wildfire spatiotemporal analysis.
The raw MODIS data contains noise and misclassified points. To enhance accuracy, fire points from 2001 to 2020 were filtered by excluding samples with confidence values below 80 and FRP below 10 (Khan et al. 2024). Points labeled as ‘active volcano’, ‘other static land source’ and ‘offshore detection’ were removed to retain only vegetation fires. Further refinement was conducted using MCD12Q1 land use data from 2001 to 2020 (https://lpdaac.usgs.gov/products/mcd12q1v006/) to exclude points in water bodies, buildings and bare land. Duplicate fire points within the same grid were also eliminated, resulting in 4824 high-quality wildfire samples for analysis.
Wildfire hazard factors in this study were selected based on their relevance to both natural and anthropogenic conditions influencing wildfire occurrence and spread. They were categorized into five types: topographic, hydrological, anthropogenic, vegetation and meteorological. Topographic factors, such as elevation and aspect, are considered to influence local microclimate, while slope and curvature influence fire spread patterns (Ghorbanzadeh et al. 2019; Yang et al. 2021; Nikolić et al. 2023). Hydrological indicators, including topographic wetness index (TWI), stream power index (SPI) and distance to rivers are used to characterize surface wetness and accessibility of water sources (Pourtaghi et al. 2015; Zhang et al. 2021). Anthropogenic factors are employed to reflect infrastructure proximity and human activity intensity, including distance to railways and highways, and nighttime lght index (NTLI) (Elia et al. 2020; Wu et al. 2023). Vegetation characteristics, such as fractional vegetation cover (FVC), determine available fuel load and combustion potential (Rihan et al. 2019; Bergonse et al. 2021b). For meteorological factors, precipitation, potential evapotranspiration and relative humidity are used to describe vegetation and environmental dryness, solar radiation determines surface heat conditions and wind speed affects fire spread behavior (Cooke et al. 2012; Bergonse et al. 2021a; de Diego et al. 2021). Information about the factors is shown in Table 1 below.
| Factor type | Factor name | Source | Format | |
|---|---|---|---|---|
| Topographic factor | Elevation | SRTM DEM (https://earthexplorer.usgs.gov) | .tif | |
| Slope | .tif | |||
| Aspect | .tif | |||
| Curvature | .tif | |||
| Hydrological factor | Topographic wetness index | .tif | ||
| Stream power index | .tif | |||
| Distance to rivers | OpenStreetMap (https://www.openstreetmap.org) | .shp | ||
| Anthropogenic factor | Distance to railways | .shp | ||
| Distance to highways | .shp | |||
| Nighttime light index | Global Change Research Data Publishing & Repository (https://www.geodoi.ac.cn/WebCn/Default.aspx) | .tif | ||
| Vegetation factor | Fractional vegetation cover | MODIS09A1 (https://lpdaac.usgs.gov/products/mod09a1v061/) | .tif | |
| Meteorological factor | Precipitation | ECMWF ERA5 Land (https://cds.climate.copernicus.eu) | .tif | |
| Solar radiation | .tif | |||
| Potential evapotranspiration | .tif | |||
| Relative humidity | .tif | |||
| Wind speed | .tif |
The selection of wildfire vulnerability and adaptive capacity factors primarily focused on socio-economic conditions and infrastructure levels, assessing both the exposure of human societies to wildfires and their ability to withstand wildfire (Xepapadeas et al. 2024). Vulnerability factors, such as population density, gross domestic product (GDP), building density, road density and railway density, reflect the risks to human life, property and regional infrastructure development. Higher population and building densities indicate increased fire exposure and potential economic loss, while dense infrastructure networks amplify vulnerability to wildfire disruptions. (Oliveira et al. 2017; de Diego et al. 2021; Xepapadeas et al. 2024). Additionally, regions with higher biodiversity values are more ecologically vulnerable to fire disturbances (Woinarski et al. 2023). Adaptive capacity factors, including per capita GDP and the proximity of fire stations and medical institutions, measure the ability to respond to and recover from wildfires. Higher GDP per capita is usually associated with more adequate resources to respond to disasters, and shorter distances to emergency services enhance the effectiveness and timeliness of interventions (Lambrou et al. 2023; Liu et al. 2024a). Infrastructure-related indicators were derived using geographic information systems (GIS) spatial analysis, where building, railroad and highway densities were calculated from vector data using kernel density tools, and proximity-based indicators were obtained using Euclidean distance functions. The information about the relevant factors is shown in Table 2.
| Factor type | Factor name | Source | Format | Direction | |
|---|---|---|---|---|---|
| Vulnerability | Population density | Resource and Environmental Science Data Platform (https://www.resdc.cn/Default.aspx) | .tif | + | |
| Gross domestic product (GDP) | .tif | + | |||
| Biodiversity values | .tif | + | |||
| Building density | OpenStreetMap (https://www.openstreetmap.org) | .shp | + | ||
| Railroad density | .shp | + | |||
| Highway density | .shp | + | |||
| Adaptive capacity | GDP per Capita | GDP/Population density | .tif | + | |
| Distance to firefighting institution | POI from Baidu Map (https://lbs.baidu.com/products/search) | .shp | − | ||
| Distance to medical institutions | .shp | − |
‘Direction’ indicates whether factor values have positive (+) or negative (−) correlation with vulnerability or adaptive capacity.
To ensure consistency in model development and statistical analysis, all factors were projected onto the UTM Zone 48N coordinate system. The data were resampled to a uniform grid size of 500 × 500 m. Subsequently, the area was divided into 2103 × 1849 grids, resulting in a total of 1,946,748 units.
Methodology
This study systematically assessed wildfire risk in Sichuan Province by integrating wildfire hazard, vulnerability and adaptive capacity across multiple quantitative models and assessment methods. The methodology comprised four steps (Fig. 2): (1) building the database for wildfire risk assessment by collecting samples of historical wildfires and related indicators; (2) using wildfire samples and the entire region as classification criteria, six quantitative connection methods were integrated with the LR model to evaluate the impact of classification criteria and connection methods on wildfire hazard modeling; (3) utilizing the TOPSIS (techniques for ranking preferences by similarity to ideal solutions) model coupled with subjective and objective combination weights to assess wildfire vulnerability and adaptive capacity; and (4) integrating hazard, vulnerability and adaptive capacity modeling results to assess the spatial distribution of wildfire risk in Sichuan Province.
Methodology flowchart (PS: probability statistics; FR: frequency ratio; IV: information value; CF: certainty factor; WOE: weights of evidence; EBF: evidential belief function; GVF: goodness-of-variance fit; VIF: variance inflation factor; EWM: entropy weight method; R = (H × V)/A: risk = (hazard × vulnerability)/ adaptive capacity).
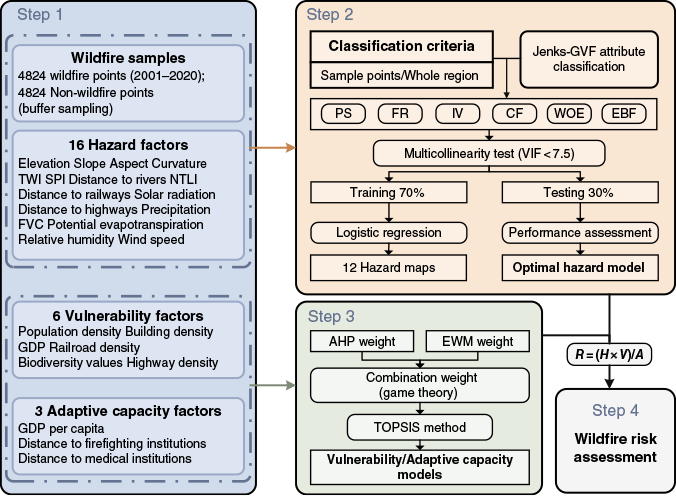
Wildfire hazard assessment methods
Six statistical connection methods, probability statistics (PS), FR, IV, certainty factor (CF), WOE and evidential belief function (EBF), were selected in this study to convert the raw attributes of factors into quantitative connection values, which were combined with the LR algorithm to construct wildfire hazard models.
PS is a common method of sample statistics. It calculates the ratio of wildfire sample points in a given interval to the total wildfire samples, reflecting the relative frequency of wildfires within that range (Huang et al. 2024).
where Ni is the number of wildfire samples in the i-th attribute interval, and N is the total number of wildfire samples in the study area.
FR is a statistical probability-based approach that compares the wildfire frequency within the specific attribute interval to its overall frequency across the area (Pourtaghi et al. 2015). The resulting ratio indicates the degree to which that interval influences wildfire hazard.
where Ni and Si denote the number of wildfire samples and total grid cells in the i-th attribute interval, while N and S represent the total wildfire samples and grid cells in the entire study area. FRi > 1 indicates the attribute interval that promotes wildfire hazard, and vice versa.
The IV assesses the impact of each attribute interval on wildfire hazard by calculating the ‘information content’ of wildfires (Polat 2021).
where the parameters are defined in the FR method. IVi > 0 indicates increased wildfire hazard, and vice versa.
The CF evaluates the influence of attribute intervals on wildfires by measuring the deviation of the conditional probability within a specific interval from the prior probability of wildfires in the study area (Hong et al. 2018).
with Pi representing the conditional probability of wildfires in the i-th interval and Ps denoting the overall wildfire occurrence probability. CFi > 0 indicates higher wildfire hazard, and vice versa.
WOE is based on Bayesian probability theory and quantifies the impact of each attribute interval on wildfires (Hong et al. 2019). It calculates the logarithmic ratio of wildfire occurrence to non-occurrence within specific intervals.
where and represent the positive and negative weights, respectively; P (B/D) is the probability of wildfires in the i-th interval; is the probability of wildfires outside that interval; and are the probabilities of no wildfires within and outside that interval, respectively. Ci > 0 indicates a positive influence on wildfire hazard, and vice versa.
EBF, based on Dempster–Shafer theory, evaluates uncertainty and heterogeneous data in spatial data integration (Nami et al. 2018). It quantifies the effect of factor conditions on wildfire hazard using belief (Bel) in the belief parameters.
where Wi represents belief weights. The higher Bel is, the greater wildfire hazard in that interval.
The delineation of factor attribute intervals and the number of classifications directly influence the ability of factors to indicate wildfire hazard (Qin et al. 2024). To ensure accuracy and objectivity, classification should be based on the actual distribution of data rather than subjective or uniform segmentation. Therefore, Jenks-GVF methodology that combines Jenks natural breaks (Jenks) and goodness-of-variance fit (GVF) was used to dynamically determine the optimal attribute classification for each hazard factor. It helps to eliminate uncertainty associated with manual subjective classification schemes.
The Jenks method classifies data by minimizing within-class variance and maximizing between-class variance (Chowdhuri et al. 2021; Rivière et al. 2023). The breakpoints were optimized to minimize the sum of squared deviations (SSD) by iteratively testing the segmentation scheme. Meanwhile, GVF was utilized to assess the classification effect by measuring the ratio of intra-class variance to total variance (Jenks and Caspall 1971):
where TV is the total variance of the dataset, and GVF ∈ [0, 1]. Higher GVF values indicate more effective classification (Fraile et al. 2016). Compared to classification methods with equal intervals or fixed thresholds, the Jenks-GVF approach better captures natural groupings within heterogeneous data distributions. In this study, the optimal number of classes was determined when the increase in GVF between successive classifications fell below 0.01, indicating that further increase in the number of classifications did not significantly improve the quality of classification. This data-adaptive and statistically grounded method ensures that the classified attribute intervals of hazard factors have higher internal consistency and external differentiation, which is particularly important for improving the interpretability of wildfire hazard modeling.
LR is a statistical model used for binary classification tasks, aiming to establish a mathematical relationship between the dependent variable and multiple independent variables, and transforming the linear model into a nonlinear probability output through the Sigmoid function (Sevgen et al. 2019). For a binary dependent variable Y (where Y ∈ [0, 1]), the predictive function is defined as:
where P(Y = 1) represents the probability that the sample belongs to class 1 (wildfire); β0 is the intercept, β1, β2, …, βn are the regression coefficients for independent variables x1, x2, …, xn, and e is the base of the natural logarithm.
The modeling dataset was constructed using connection values of the factors as inputs and the sample attributes as outputs (1 for wildfire; 0 for non-wildfire). The dataset was randomly split into a training set (70%) and a testing set (30%), maintaining a balanced ratio of positive and negative samples: 3376:3377 for training and 1448:1447 for testing. During training, the 10-fold cross-validation method was used to ensure the robustness and generalization ability of the model (Bera et al. 2022).
The receiver operating characteristic (ROC) curve visualizes the model’s classification ability at different decision thresholds by plotting the true positive rate against the false positive rate. The area under the curve (AUC) value ranges from [0, 1]. The closer the AUC value is to 1, the better the model’s overall classification performance (Dehnavi et al. 2015). Beyond the ROC curve, additional metrics such as precision, recall, F1-score and accuracy further evaluate the classification performance from multiple perspectives, offering a more comprehensive assessment of the predictive performance of model (Hang et al. 2024).
Vulnerability and adaptive capacity assessment methods
The TOPSIS model and factor weights were used in this study to assess vulnerability and adaptive capacity. As a widely used multi-criteria evaluation method, the core principle of TOPSIS is to assess the relative superiority or inferiority of each evaluation object by calculating its respective distances from the positive ideal solution and the negative ideal solution (Jena and Pradhan 2020; Xiao et al. 2022). The calculation process is as follows:
(1) Standardize the indicator with different dimensions to obtain the standardized value .
(2) Apply the weight Wj to each indicator, resulting in a weighted standardized matrix z = [zij].
(3) Define the positive ideal solution A+ and the negative ideal solution A−, representing the best and worst values for each indicator, respectively.
(4) Compute the Euclidean distance between each evaluation object and the positive ideal solution and the negative ideal solution .
(5) Based on the distances from the ideal solutions, calculate the relative closeness Ci of each object. The closer the value is to 1, the higher the vulnerability or adaptive capacity of the object.
The AHP-EWM (entropy weight method) subjective-objective combination weighting method based on game theory was used to calculate the factor weights. Among them, the AHP method incorporates expert experience and decision preferences through pairwise comparisons between factors, while the EWM method objectively reflects the inherent variability of each indicator based on the actual data distribution. This combination makes it possible to balance subjective judgment and objective data when assigning factor importance. The calculation formula are as follows:
where winitial is the initial combined weight; wAHP and wEWM are subjective and objective weights, respectively; β1 and β2 are the weighting coefficients, with initial values set at 0.5. Then, the weight coefficients β1 and β2 are optimized by defining the objective function Error to minimize the error of the linear combination of weights with respect to the target weights wq. Finally, through iterative optimization, the final weighting coefficients and are obtained and used to linearly combine wAHP and wEWM, producing the final combined weight W.
Wildfire risk assessment method
Risk assessment is defined as the degree of hazard of the disaster event, the degree of exposure of people and property to the hazard, and consequences of the exposure (Lirer and Vitelli 1998; Hu et al. 2009). In this study, the wildfire risk was positively correlated with hazard and vulnerability, and negatively correlated with adaptive capacity. The formula is shown below:
Results
Wildfire hazard modeling and assessment
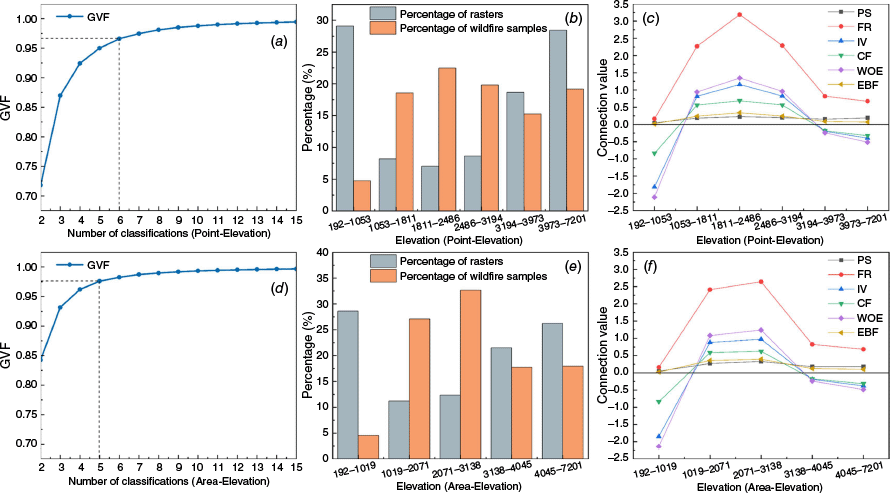
The Jenks-GVF method was used to determine the optimal number of classes and attribute intervals for each factor, using both wildfire samples and the whole area as classification criteria. Using elevation as an example (Fig. 3), the GVF curves (first column) showed a rapid increase followed by a plateau as the number of classes increased, indicating diminishing marginal gains in explanatory power. The optimal number of classes was six based on wildfire samples and five based on the whole area. The second and third columns present the area proportion, wildfire sample percentage and connection values (PS, FR, IV, CF, WOE, EBF) across classification intervals. It can be seen that the classification criteria directly influence the number of factor attribute intervals and the distribution of connection values, which in turn affects their ability to distinguish wildfire hazard levels.
Elevation classification and connection value calculation results based on different classification bases. Subfigures (a–c) present the GVF curves, subdivision areas, and wildfire sample coverage under optimal classification using wildfire samples as criteria. Subfigures (d–f) show the same metrics using the whole area as classification criteria (GVF: goodness-of-variance fit; PS: probability statistics; FR: frequncy ratio; IV: information value; CF: certainty factor; WOE: weights of evidence; EBF: evidential belief function).
Wildfire hazard values were predicted and visualized for the whole area based on LR models constructed with different classification criteria and connection values. All visual maps of wildfire hazard were classified into five levels using consistent equal-interval classification schemes: very low ((0, 0.20]), low ((0.20, 0.40]), moderate ((0.40, 0.60]), high ((0.60, 0.80]) and very high ((0.80, 1.00]) (Fig. 4). This ensures that each level corresponds to a fixed numerical range, facilitating clear comparison between hazard maps derived from different models and reducing classification ambiguity. Visually, the overall wildfire hazard has similar spatial distribution across the models, with high hazard areas concentrated in the southwestern and some western mountainous regions, and low hazard areas in the plateau and plains of northwestern and eastern Sichuan. Hazard levels exhibited clear gradients from extremely high to extremely low hazard zones. However, the hazard zoning results of PS, FR and EBF models constructed based on different classification criteria varied significantly. In contrast, the IV, CF and WOE models exhibited smaller differences and maintained consistent clustering with higher stability.
Wildfire hazard maps generated using different connection methods coupled with the logistic regression (LR) algorithm. Subfigures (a–f) are based on wildfire samples as classification criteria of factor attributes, and subfigures (g–l) are based on the whole area (PS: probability statistics; FR: frequncy ratio; IV: information value; CF: certainty factor; WOE: weights of evidence; EBF: evidential belief function).
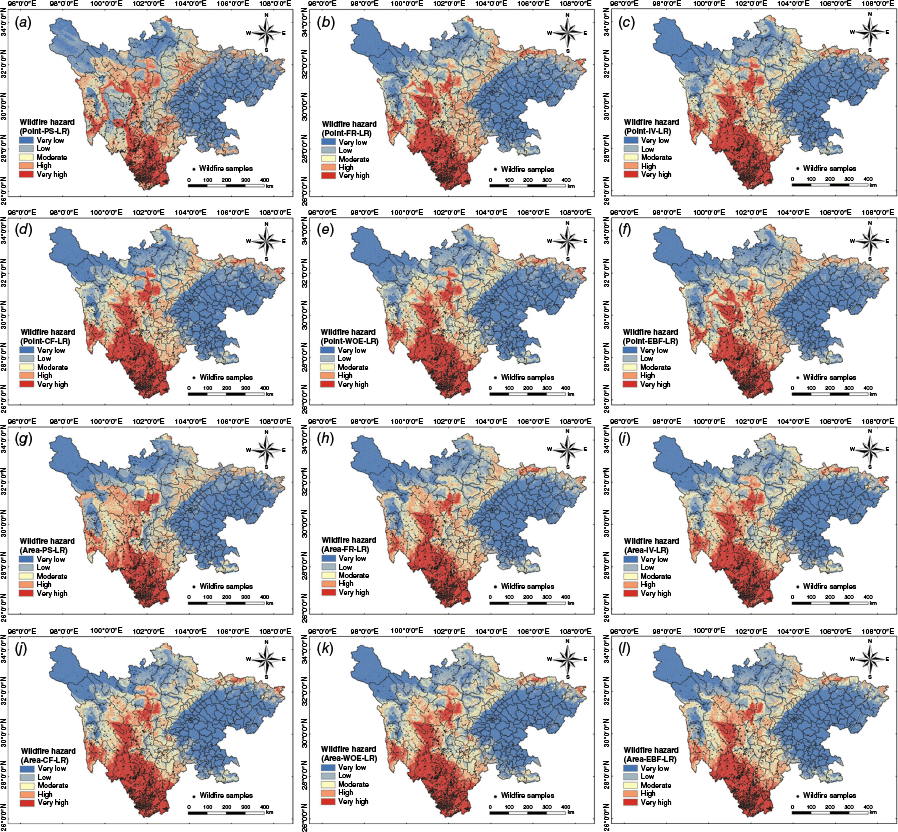
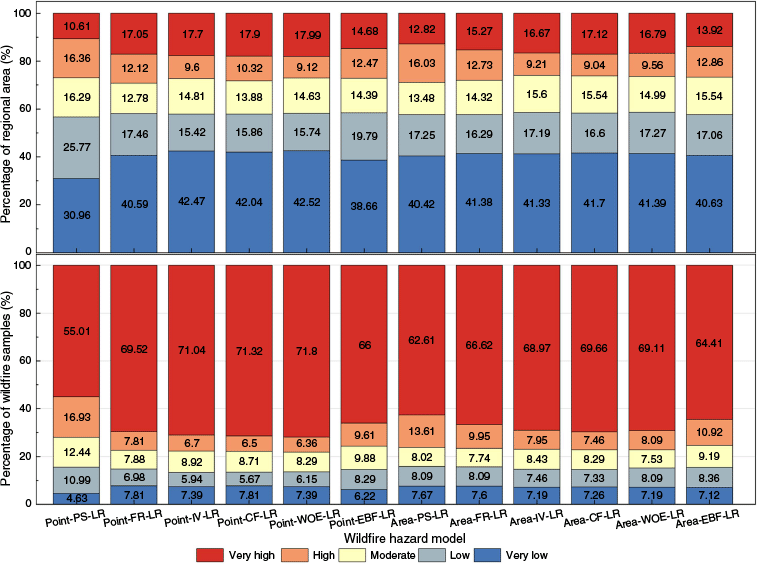
As shown in Fig. 5, the models based on wildfire samples classification had higher proportions of very high and very low hazard areas, better capturing wildfire-prone regions while reducing misclassification of low hazard areas. IV, CF and WOE models consistently identified larger very high hazard areas under both classification criteria, showing greater stability. PS, FR and EBF models displayed more variability, with greater fluctuations in hazard area distribution.
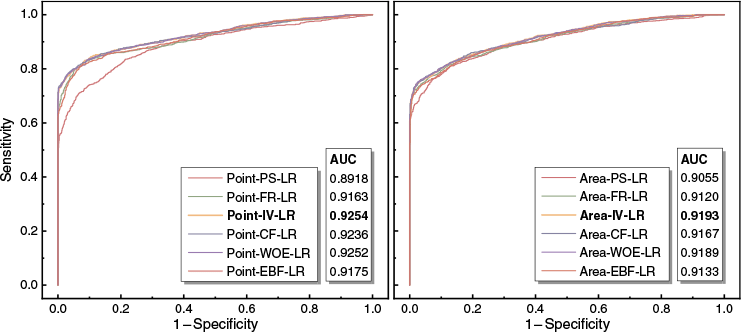
The ROC curves and AUC values for each model on the test set are shown in Fig. 6. Except for PS, models classified based on sample points had higher AUC values than those classified based on the whole area. It can be seen that classification based on sample points better captures wildfire distribution characteristics, enhancing overall classification performance, while models classified based on the whole region show limitations in distinguishing high and low hazard areas. Among connection methods, models using IV performed best under both classification criteria, achieving the highest AUC values, followed by WOE, CF, EBF, FR, and PS. The Point-IV-LR model, classified based on wildfire sample points, had the highest AUC value (0.9254), demonstrating the best predictive performance.
Receiver operating characteristic curves and area under the curve values for hazard models (PS: probability statistics; FR: frequncy ratio; IV: information value; CF: certainty factor; WOE: weights of evidence; EBF: evidential belief function; LR: logistic regression).
As shown in Fig. 7, all metrics for the models based on wildfire sample classification outperformed for those based on whole area classification, except for PS. Moreover, Point-IV-LR, Point-CF-LR and Point-WOE-LR outperformed the other models. The Point-IV-LR model achieved the highest recall, F1-score and accuracy, demonstrating superior balance in classification precision and wildfire sample identification. The Point-EBF-LR model had the highest precision, effectively identifying high hazard areas while minimizing misclassification of low hazard areas.
Receiver operating characteristic curves and area under the curve values for hazard models (PS: probability statistics; FR: frequncy ratio; IV: information value; CF: certainty factor; WOE: weights of evidence; EBF: evidential belief function; LR: logistic regression).
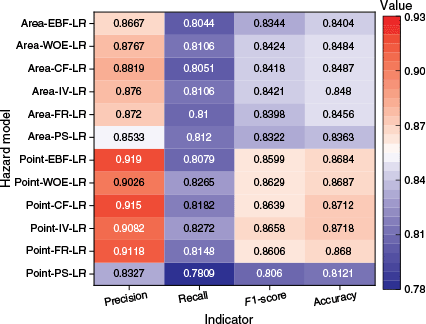
Overall, models classified based on wildfire sample points, particularly when using IV, CF and WOE, demonstrated stability and superior performance. The Point-IV-LR model emerged as the most effective for wildfire hazard assessment, providing a reliable foundation for subsequent risk assessment.
As shown in Fig. 8, elevation, TWI, distance to railways, solar radiation and potential evapotranspiration consistently ranked high in factor importance across most models, highlighting their critical roles in wildfire hazard. Elevation is thought to influence the local microclimate and vegetation zone, which determines fuel availability and flammability. TWI represents the spatial distribution of soil moisture influenced by terrain, which affects how readily vegetation can dry and ignite. Distance to railroads is commonly used to reflect the intensity of human activities affecting wildfires. Solar radiation is considered to affect vegetation dryness, thereby altering ignition potential and combustion behavior. Potential evapotranspiration indicates atmospheric moisture demand and strongly regulates fuel dryness conditions. Notably, solar radiation and potential evapotranspiration are consistently assigned high importance across most models, suggesting that surface dryness and changes in fuel loads have significant impact on the occurrence and spread of wildfires.
Factor significance of the models. Where Dis_riv: Distance to rivers; Dis_rail: Distance to railways; Hum_act: Human activities; Sol_rad: Solar radiation; Pot_eva: Potential evapotranspiration; Rel_hum: Relative humidity; Others: the remaining nine factors; FVC: fractional vegetation cover; SPI: stream power index; TWI: topographic wetness index.
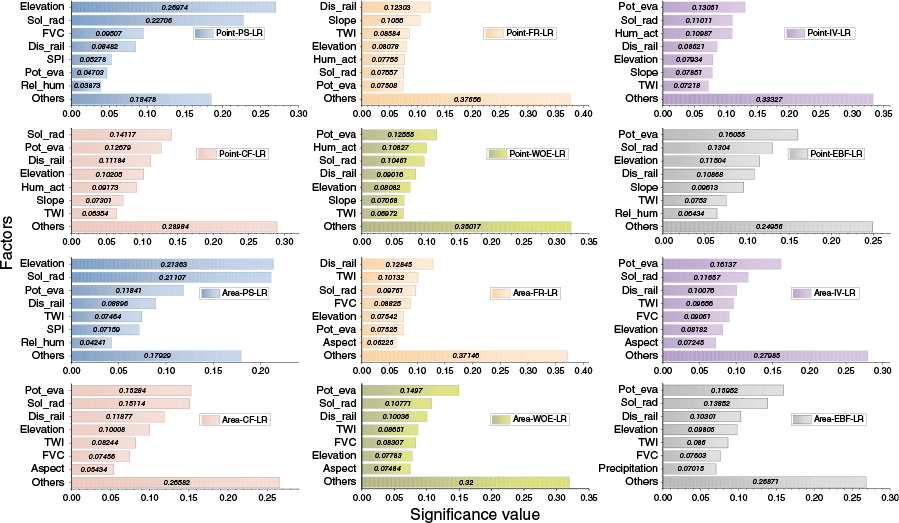
In addition, the models using IV, CF and WOE exhibited high consistency compared to PS, FR and EBF, with the top seven factors being nearly identical with minimal differences in rankings. In models classified based on wildfire samples, the most important factors were elevation, slope, TWI, distance to railways, human activities, solar radiation and potential evapotranspiration. For whole area classification, the top factors were elevation, aspect, TWI, distance to railways, FVC, solar radiation and potential evapotranspiration.
Attribute intervals and corresponding IV values of factors were used to reveal the effects on wildfire hazard based on the optimal Point-IV-LR model (Figs 9, 10).
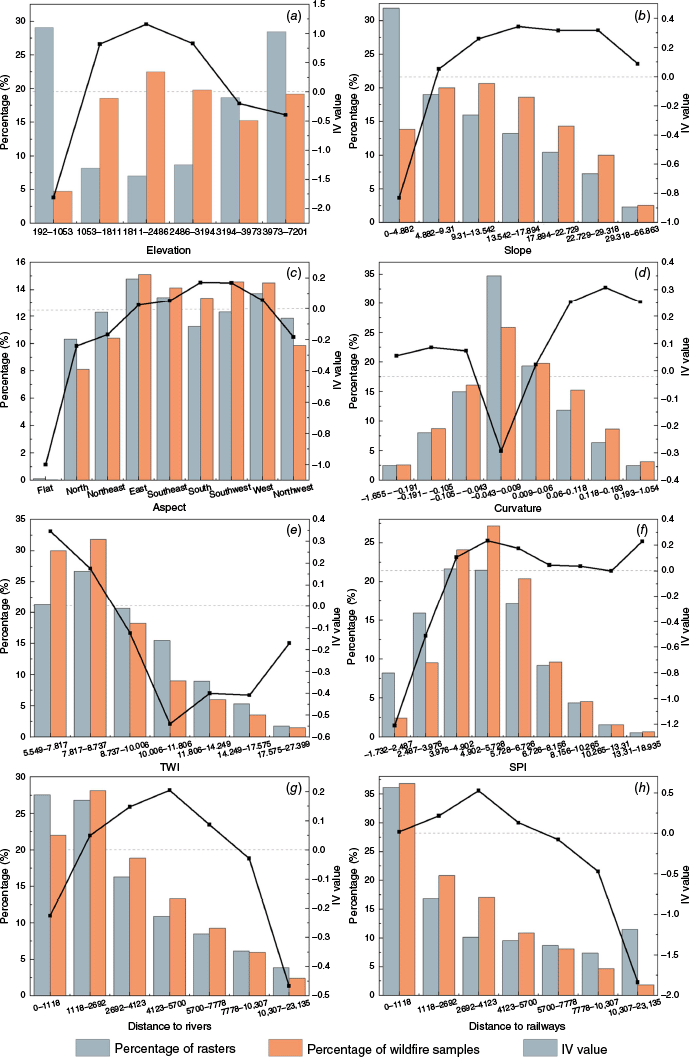
Information values (IV) for different attribute intervals of each factor: (a–d) topographic factors (elevation, slope, aspect, curvature); (e–g) hydrological factors (topographic wetness index (TWI), stream power index (SPI), distance to rivers); (h) anthropogenic factor (distance to railways).
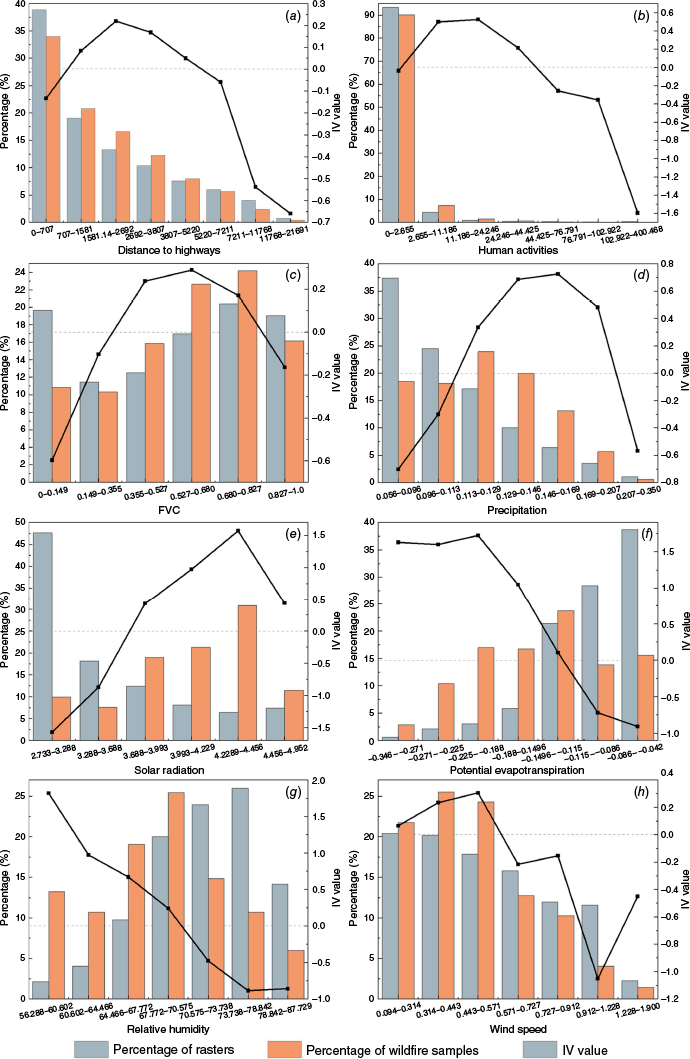
Information values (IV) for different attribute intervals of each factor: (a–b) anthropogenic factor (distance to highways, human activities); (c) vegetation factor (fractional vegetation cover (FVC)); (d–h) meteorological factors (precipitation, solar radiation, potential evapotranspiration, relative humidity, wind speed).
For topographic factors, IV values for elevation were positive in the range of (120, 1150 m], where elevation may create the moderate temperature microclimate and vegetation type favorable for wildfires. Positive IV values for the slope factor in the range of (4.882°, –66.863°], suggesting that steeper terrain facilitated wildfire spread. Positive IV values for east, southeast, south, southwest and west aspects reflected increased solar exposure on these slopes, leading to drier surface conditions. Positive IV values were observed when the absolute value of curvature was greater than 0.043, possibly because undulating terrain can accumulate dry fuels and support flame propagation.
For hydrological factors, the influence of TWI on wildfire hazard generally declined, while SPI tended to increase. Positive IV values were observed for TWI in (5.549, 8.737] and SPI in (3.976, 18.935], suggesting that higher flow intensity and lower topographic moisture favored wildfire occurrence and spread. Distance to rivers exhibited an inverted U-shaped trend with positive IV values in (1118, 7778 m], likely due to limited water availability and specific vegetation distributions.
For anthropogenic factors, wildfire samples were densely distributed within [0, 5700 m] from railways with positive IV values. Although the IV value was negative at [0, 707 m] distance from the highway, this range contained the highest number of wildfire samples. In (707, 5220 m], the IV value turned positive, suggesting increased wildfire hazard due to human activity. Similarly, the NTLI had negative IV values at [0, 2.655], which covered nearly 90% of wildfire samples, while positive IV values in (2.655, 44.425] indicating increased wildfire hazards from increased human activity. The IV for FVC was positive at (0.149, 0.827], indicating the areas typically have sufficient combustible material for higher wildfire hazard.
For meteorological factors, precipitation exhibited an increasing then decreasing trend, with positive IV values at (0.113, 0.207 m]. It may be due to the fact that moderate precipitation promotes vegetation growth without significantly increasing ambient humidity, which promotes wildfire hazard. Solar radiation showed an overall positive correlation with wildfire hazard. It may facilitate wildfire occurrence and spread by enhancing surface heating and fuel drying. In contrast, potential evapotranspiration and relative humidity were negatively correlated with wildfire hazard, indicating that high surface evaporation and low air humidity increase wildfire hazard. Positive IV values for wind speeds in the range of [0.094, 0.571 m/s] suggest that low wind speeds can promote wildfire spread by allowing heat to build up locally and trapping embers in forest combustibles.
Wildfire vulnerability and adaptive capacity modeling and assessment
The AHP, EWM and AHP-EWM combination weights for each factor are shown in Table 3. Among the vulnerability factors, GDP had the highest weight, reflecting the significant economic losses wildfires cause at the regional level. Biodiversity value also received a high weight, highlighting the severe damage in ecologically sensitive areas. Railroad density and population density were equally important for assessing human exposure risks and infrastructure vulnerability, while highway density and building density had relatively lower impacts. For adaptive capacity factors, distance to firefighting institutions had the highest weight, emphasizing the critical role of firefighting resource accessibility in emergency response. The weights of distance to medical facilities and GDP per capita indicate their importance in emergency response and disaster recovery.
| Factor type | Factor name | w AHP | w EWM | W | |
|---|---|---|---|---|---|
| Vulnerability | Population density | 0.193 | 0.186 | 0.189 | |
| Gross domestic product (GDP) | 0.193 | 0.28 | 0.242 | ||
| Building density | 0.078 | 0.127 | 0.106 | ||
| Railroad density | 0.036 | 0.259 | 0.161 | ||
| Highway density | 0.078 | 0.085 | 0.082 | ||
| Biodiversity value | 0.42 | 0.064 | 0.22 | ||
| Adaptive capacity | GDP per capita | 0.443 | 0.01 | 0.256 | |
| Distance to firefighting institutions | 0.387 | 0.469 | 0.423 | ||
| Distance to medical institutions | 0.169 | 0.521 | 0.322 |
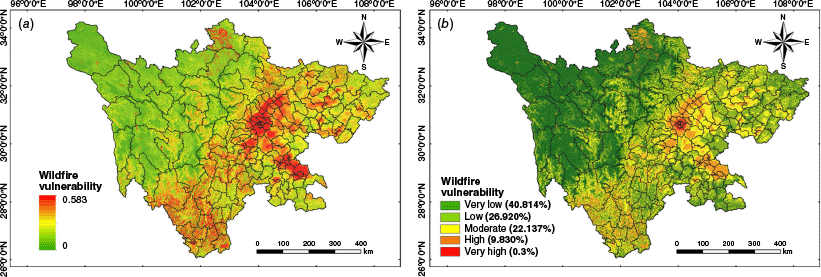
Wildfire vulnerability maps were generated using the TOPSIS model combined with AHP-EWM weights (Fig. 11). The regional vulnerability generally followed a ‘high in the southeast, low in the northwest’ pattern, displaying clear spatial heterogeneity. The very high vulnerability areas accounted for only 0.3% of the total area, mainly in Chengdu, a densely populated and economically developed region. High vulnerability areas covered 9.83%, mainly in the ecologically sensitive southwestern Sichuan and urbanized central and southeastern regions. Moderate vulnerability areas made up 22.137%, scattered mainly across central and eastern Sichuan’s hilly and plain areas. Very low and low vulnerability areas comprised 67.734% of the total area, primarily distributed across the sparsely populated northwestern plateau with limited socio-economic development and lower ecosystem valuation.
Adaptive capacity exhibited a spatial pattern of ‘strong in the east, weak in the west’ (Fig. 12). The very high and high adaptive capacity areas were concentrated in the urbanized regions of central and southern Sichuan, where higher per capita GDP and proximity to medical and firefighting institutions enhanced disaster response and recovery. Moderate adaptive capacity areas, accounting for 33.321%, were mainly in the moderately developed regions of central and southern Sichuan. Low and very low adaptive capacity areas accounted for 26.981%, mainly concentrated in the remote mountainous regions of western and northwestern Sichuan, where low economic levels and insufficient firefighting and medical infrastructures hindered emergency response and resource mobilization in the event of wildfires.
Wildfire risk modeling and assessment
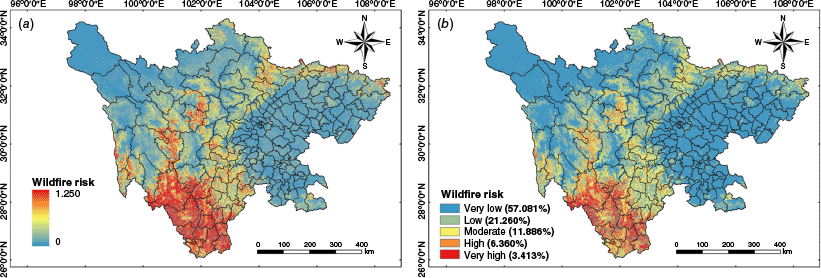
The wildfire risk assessment results revealed clear spatial heterogeneity, with risk levels increasing from northeast to southwest (Fig. 13). Very low and low risk areas covered 78.341% of the region. In the northwest, including areas such as northwestern Ganzi and central to northern Aba, wildfire hazard was minimal due to sparse population, limited socio-economic activity and stable ecological conditions, resulting in low exposure and losses. Eastern Sichuan, including Chengdu and its southern, eastern and northeastern surrounding cities, had higher population density and human activity, increasing vulnerability. However, lower hazard levels and stronger emergency response capacity helped reduce overall risk.
Moderate risk areas were mainly located in central and south-central Sichuan, accounting for 11.886% of the area. These regions are ecologically sensitive and experiencing urban expansion. While hazard and vulnerability were moderate, high adaptive capacity mitigated potential impacts.
High and very high risk areas were concentrated in the southwestern mountains, including Panzhihua and western to southern Liangshan, accounting for 9.773% of the area. These areas are marked by rugged terrain, abundant combustible vegetation and high ecological value. Combined with limited transportation access and weaker emergency response capacity, these conditions lead to significant wildfire risk and greater difficulty in mitigation and response.
To validate the rationality of the wildfire risk zoning, the FR value of each risk level was calculated. As shown in Table 4, FR values increase with higher risk levels, and the high and very high zones show significantly higher values than 1.0. It validates the reliability of the risk assessment results.
Discussion
In recent years, several independent statistical connection methods have been employed by many researchers in wildfire hazard modeling (Pourghasemi 2016; Hong et al. 2019; Arca et al. 2020; de Santana et al. 2021), and their predictive performance has been studied comparatively (Abedi Gheshlaghi et al. 2021; Salavati et al. 2022; Das et al. 2023). To improve accuracy, integrated approaches that combine these methods with variable interaction algorithms such as LR, random forest and support vector machine have gained traction (Hong et al. 2018; Jaafari et al. 2019; Hosseini and Lim 2022). In contrast to previous studies focusing on comparing a limited number of integrated models, six widely used connection methods (PS, FR, IV, CF, WOE, EBF) integrated with LR were systematically assessed in this study and their different impacts on hazard prediction were analyzed. Additionally, novel comparisons were made between two classification criteria of factor attributes. Classification based on wildfire samples is more specific to actual wildfire zones than classification based on whole area, resulting in better model accuracy and more targeted hazard mapping, while also improving computational efficiency. Unlike the GeoDetector used by Wang et al. (2024) to optimize interval delineation in the WOE model, the Jenks-GVF method was used for automated classification, enabling a deeper evaluation of classification criteria on model performance. Jenks-GVF highlights the natural distribution of the data, avoids the heterogeneity of classification methods among different factors and ensures better interpretability of the classification results of factors.
Based on this, Sichuan Province was selected for integrated modeling and spatial analysis. The results revealed significantly high wildfire hazard in the southwest, particularly in Liangshan and Panzhihua, aligning with previous studies (Peng et al. 2023; Liu et al. 2024b). Despite differences in sampling, factor selection and evaluation methods, both identify surface temperature and humidity conditions, elevation and human activity as key factors influencing the spatial distribution of wildfires. Prior studies employing various ML approaches in Sichuan have enhanced hazard prediction accuracy (Tian et al. 2022; Chen et al. 2023; Peng et al. 2023; Ji et al. 2024). However, these models often faced the trade-off between accuracy and interpretability, as increased complexity reduced the transparency of factor-driven effects (Phelps and Woolford 2021). For this reason, statistical connection methods were integrated with LR to balance performance and interpretability – preserving internal attribute insights while enabling quantitative factor analysis. Furthermore, this study extended beyond hazard mapping by incorporating a comprehensive risk framework based on f(hazard, vulnerability, adaptive capacity), facilitating multidimensional analysis of wildfire risk, potential impact and adaptive capacity across Sichuan.
Nonetheless, this study also has limitations. First, the vulnerability and adaptive capacity indicators lacked comprehensive coverage of complex dimensions such as vulnerable populations, infrastructure, socio-economic conditions and emergency service accessibility. Future work should integrate multi-source socio-economic data to enhance realistic relevance. Second, the assumption of temporal stationarity may oversimplify reality, as some wildfire drivers often exhibit significant temporal variability characteristics (Su et al. 2024). Finer temporal resolution vegetation and meteorological data could be incorporated to enhance the dynamic modeling of wildfire ignition probability and fire behavior in time series frameworks. Third, advanced modeling approaches such as Bayesian Networks may be introduced to improve probabilistic reasoning, address variable interdependencies, and better handle uncertainty in future wildfire risk assessment.
Conclusion
This study systematically analyzed the effects of different connection methods coupled with LR model on the wildfire hazard assessment under different classification criteria of factor attributes. Additionally, vulnerability and adaptive capacity models were integrated with the optimal hazard model to conduct comprehensive spatial assessment of wildfire risk. The main findings are as follows:
The classification criteria and connection methods significantly influenced predictive performance and spatial distribution of wildfire hazard. Models based on IV, CF and WOE demonstrated high stability and accuracy, with the Point-IV-LR model performing best. High wildfire hazard areas were concentrated in the southwestern and western mountainous regions, while low hazard areas were mainly in the northwestern plateau and eastern plains. Elevation, slope, TWI, distance to railways, human activities, solar radiation and potential evapotranspiration were key contributing factors.
High vulnerability was found in urbanized central and eastern Sichuan and ecologically sensitive southwestern areas, while low vulnerability was found in the northwestern plateau. High adaptive capacity was found in economically developed areas in the central and eastern parts of the region, and low adaptive capacity was found in remote mountainous areas and plateau areas in the west.
High risk areas were concentrated in the southwestern region, while the eastern and northwestern regions had lower risks. Mountainous and ecologically sensitive areas in southwestern Sichuan, where wildfire hazard and vulnerability were high but adaptive capacity was weak, were identified as critical zones for future wildfire prevention.
Declaration of funding
The work reported was supported by National Key R&D Program of China (No. 2022YFC3005704), National Natural Science Foundation of China (No. 52278415), Sichuan Science and Technology Program (No. 2024YFFK0111), Sichuan Fire Research Institute of MEM Science and Technology Projects (No. 20248815Z).
Acknowledgements
The authors gratefully acknowledge the fire data acquired from NASA’s FIRMS platform.
References
Abedi Gheshlaghi H, Feizizadeh B, Blaschke T, Lakes T, Tajbar S (2021) Forest fire susceptibility modeling using hybrid approaches. Transactions in GIS 25(1), 311-333.
| Crossref | Google Scholar |
Arca D, Hacısalihoğlu M, Kutoğlu ŞH (2020) Producing forest fire susceptibility map via multi-criteria decision analysis and frequency ratio methods. Natural Hazards 104, 73-89.
| Crossref | Google Scholar |
Bera B, Shit PK, Sengupta N, Saha S, Bhattacharjee S (2022) Forest fire susceptibility prediction using machine learning models with resampling algorithms, northern part of Eastern Ghat Mountain range (India). Geocarto International 37(26), 11756-11781.
| Crossref | Google Scholar |
Bergonse R, Oliveira S, Gonçalves A, Nunes S, da Câmara C, Zêzere JL (2021a) A combined structural and seasonal approach to assess wildfire susceptibility and hazard in summertime. Natural Hazards 106, 2545-2573.
| Crossref | Google Scholar |
Bergonse R, Oliveira S, Gonçalves A, Nunes S, DaCamara C, Zêzere JL (2021b) Predicting burnt areas during the summer season in Portugal by combining wildfire susceptibility and spring meteorological conditions. Geomatics, Natural Hazards and Risk 12(1), 1039-1057.
| Crossref | Google Scholar |
Bui DT, Bui Q-T, Nguyen Q-P, Pradhan B, Nampak H, Trinh PT (2017) A hybrid artificial intelligence approach using GIS-based neural-fuzzy inference system and particle swarm optimization for forest fire susceptibility modeling at a tropical area. Agricultural and Forest Meteorology 233, 32-44.
| Crossref | Google Scholar |
Cao Y, Wang M, Liu K (2017) Wildfire susceptibility assessment in Southern China: a comparison of multiple methods. International Journal of Disaster Risk Science 8, 164-181.
| Crossref | Google Scholar |
Chen R, He B, Quan X, Lai X, Fan C (2023) Improving wildfire probability modeling by integrating dynamic-step weather variables over Northwestern Sichuan, China. International Journal of Disaster Risk Science 14(2), 313-325.
| Crossref | Google Scholar |
Chowdhuri I, Pal SC, Chakrabortty R, Malik S, Das B, Roy P (2021) Torrential rainfall-induced landslide susceptibility assessment using machine learning and statistical methods of eastern Himalaya. Natural Hazards 107, 697-722.
| Crossref | Google Scholar |
Cooke WH, Mostovoy GV, Anantharaj VG, Jolly WM (2012) Wildfire potential mapping over the state of Mississippi: a land surface modeling approach. GIScience & Remote Sensing 49(4), 492-509.
| Crossref | Google Scholar |
Cunningham CX, Williamson GJ, Bowman DM (2024) Increasing frequency and intensity of the most extreme wildfires on Earth. Nature Ecology & Evolution 8(8), 1420-1425.
| Crossref | Google Scholar | PubMed |
Das J, Mahato S, Joshi PK, Liou Y-A (2023) Forest fire susceptibility zonation in Eastern India using statistical and weighted modelling approaches. Remote Sensing 15(5), 1340.
| Crossref | Google Scholar |
de Diego J, Rúa A, Fernández M (2021) Vulnerability variables and their effect on wildfires in Galicia (Spain). A panel data analysis. Land 10(10), 1004.
| Crossref | Google Scholar |
Dehnavi A, Aghdam IN, Pradhan B, Varzandeh MHM (2015) A new hybrid model using step-wise weight assessment ratio analysis (SWARA) technique and adaptive neuro-fuzzy inference system (ANFIS) for regional landslide hazard assessment in Iran. Catena 135, 122-148.
| Crossref | Google Scholar |
de Santana RO, Delgado RC, Schiavetti A (2021) Modeling susceptibility to forest fires in the Central Corridor of the Atlantic Forest using the frequency ratio method. Journal of Environmental Management 296, 113343.
| Crossref | Google Scholar | PubMed |
Elia M, D’Este M, Ascoli D, Giannico V, Spano G, Ganga A, Colangelo G, Lafortezza R, Sanesi G (2020) Estimating the probability of wildfire occurrence in Mediterranean landscapes using Artificial Neural Networks. Environmental Impact Assessment Review 85, 106474.
| Crossref | Google Scholar |
Erdin C, Çağlar M (2021) Rural fire risk assessment in GIS environment using fuzzy logic and the AHP approaches. Polish Journal of Environmental Studies 30(6), 4971-4984.
| Crossref | Google Scholar |
Fedeski M, Gwilliam J (2007) Urban sustainability in the presence of flood and geological hazards: the development of a GIS-based vulnerability and risk assessment methodology. Landscape and Urban Planning 83(1), 50-61.
| Crossref | Google Scholar |
Fraile A, Larrodé E, Magrenán ÁA, Sicilia JA (2016) Decision model for siting transport and logistic facilities in urban environments: a methodological approach. Journal of Computational and Applied Mathematics 291, 478-487.
| Crossref | Google Scholar |
Ghorbanzadeh O, Valizadeh Kamran K, Blaschke T, Aryal J, Naboureh A, Einali J, Bian J (2019) Spatial prediction of wildfire susceptibility using field survey GPS data and machine learning approaches. Fire 2(3), 43.
| Crossref | Google Scholar |
Guo H, Gao Y, Ye Z, Yang Z, Zhang Y, Lei Z, Sun A (2025) Experimental investigation of fire behaviours and heat transfer in single cypress tree crown fires. International Journal of Wildland Fire 34(2), WF24030.
| Crossref | Google Scholar |
Hang HT, Mallick J, Alqadhi S, Bindajam AA, Abdo HG (2024) Exploring forest fire susceptibility and management strategies in Western Himalaya: integrating ensemble machine learning and explainable AI for accurate prediction and comprehensive analysis. Environmental Technology & Innovation 35, 103655.
| Crossref | Google Scholar |
Hong H, Naghibi SA, Moradi Dashtpagerdi M, Pourghasemi HR, Chen W (2017) A comparative assessment between linear and quadratic discriminant analyses (LDA-QDA) with frequency ratio and weights-of-evidence models for forest fire susceptibility mapping in China. Arabian Journal of Geosciences 10, 1-14.
| Crossref | Google Scholar |
Hong H, Tsangaratos P, Ilia I, Liu J, Zhu A-X, Xu C (2018) Applying genetic algorithms to set the optimal combination of forest fire related variables and model forest fire susceptibility based on data mining models. The case of Dayu County, China. Science of The Total Environment 630, 1044-1056.
| Crossref | Google Scholar | PubMed |
Hong H, Jaafari A, Zenner EK (2019) Predicting spatial patterns of wildfire susceptibility in the Huichang County, China: an integrated model to analysis of landscape indicators. Ecological Indicators 101, 878-891.
| Crossref | Google Scholar |
Hosseini M, Lim S (2022) Gene expression programming and data mining methods for bushfire susceptibility mapping in New South Wales, Australia. Natural Hazards 113(2), 1349-1365.
| Crossref | Google Scholar |
Hu B, Zhou J, Wang J, Chen Z, Wang D, Xu S (2009) Risk assessment of land subsidence at Tianjin coastal area in China. Environmental Earth Sciences 59, 269-276.
| Crossref | Google Scholar |
Huang F, Xiong H, Zhou X, Catani F, Huang J (2024) Modelling uncertainties and sensitivity analysis of landslide susceptibility prediction under different environmental factor connection methods and machine learning models. KSCE Journal of Civil Engineering 28(1), 45-62.
| Crossref | Google Scholar |
Jaafari A, Zenner EK, Pham BT (2018) Wildfire spatial pattern analysis in the Zagros Mountains, Iran: a comparative study of decision tree based classifiers. Ecological Informatics 43, 200-211.
| Crossref | Google Scholar |
Jaafari A, Mafi-Gholami D, Thai Pham B, Tien Bui D (2019) Wildfire probability mapping: bivariate vs. multivariate statistics. Remote Sensing 11(6), 618.
| Crossref | Google Scholar |
Jena R, Pradhan B (2020) Integrated ANN-cross-validation and AHP-TOPSIS model to improve earthquake risk assessment. International Journal of Disaster Risk Reduction 50, 101723.
| Crossref | Google Scholar |
Jenks GF, Caspall FC (1971) Error on choroplethic maps: definition, measurement, reduction. Annals of the Association of American Geographers 61(2), 217-244.
| Google Scholar |
Ji C, Yang H, Li X, Pei X, Li M, Yuan H, Cao Y, Chen B, Qu S, Zhang N (2024) Forest wildfire risk assessment of Anning River Valley in Sichuan Province based on driving factors with multi-source data. Forests 15(9), 1523.
| Crossref | Google Scholar |
Joyce J, Chang N-B, Harji R, Ruppert T (2018) Coupling infrastructure resilience and flood risk assessment via copulas analyses for a coastal green-grey-blue drainage system under extreme weather events. Environmental Modelling & Software 100, 82-103.
| Crossref | Google Scholar |
Ke C, He S, Qin Y (2023) Comparison of natural breaks method and frequency ratio dividing attribute intervals for landslide susceptibility mapping. Bulletin of Engineering Geology and the Environment 82(10), 384.
| Crossref | Google Scholar |
Khan MA, Gupta A, Sharma P, Roy A (2024) Investigation of wildfire risk and its mapping using GIS-integrated AHP method: a case study over Hoshangabad Forest Division in Central India. Environment, Development and Sustainability 1-35.
| Crossref | Google Scholar |
Lambrou N, Kolden C, Loukaitou-Sideris A, Anjum E, Acey C (2023) Social drivers of vulnerability to wildfire disasters: a review of the literature. Landscape and Urban Planning 237, 104797.
| Crossref | Google Scholar |
Li F, Zhang X, Kondragunta S, Csiszar I (2018) Comparison of fire radiative power estimates from VIIRS and MODIS observations. Journal of Geophysical Research: Atmospheres 123(9), 4545-4563.
| Crossref | Google Scholar |
Lirer L, Vitelli L (1998) Volcanic risk assessment and mapping in the Vesuvian area using GIS. Natural Hazards 17, 1-15.
| Crossref | Google Scholar |
Liu J, Tan L, Ma Y (2024a) An integrated risk assessment method for urban areas due to chemical leakage accidents. Reliability Engineering & System Safety 247, 110091.
| Crossref | Google Scholar |
Liu J, Wang Y, Lu Y, Zhao P, Wang S, Sun Y, Luo Y (2024b) Application of remote sensing and Explainable Artificial Intelligence (XAI) for wildfire occurrence mapping in the mountainous region of southwest China. Remote Sensing 16(19), 3602.
| Crossref | Google Scholar |
Naderpour M, Rizeei HM, Khakzad N, Pradhan B (2019) Forest fire induced Natech risk assessment: a survey of geospatial technologies. Reliability Engineering & System Safety 191, 106558.
| Crossref | Google Scholar |
Nami M, Jaafari A, Fallah M, Nabiuni S (2018) Spatial prediction of wildfire probability in the Hyrcanian ecoregion using evidential belief function model and GIS. International Journal of Environmental Science and Technology 15, 373-384.
| Crossref | Google Scholar |
Nasiri V, Sadeghi SMM, Bagherabadi R, Moradi F, Deljouei A, Borz SA (2022) Modeling wildfire risk in western Iran based on the integration of AHP and GIS. Environmental Monitoring and Assessment 194(9), 644.
| Crossref | Google Scholar | PubMed |
Nguyen K-A, Liou Y-A, Terry JP (2019) Vulnerability of Vietnam to typhoons: a spatial assessment based on hazards, exposure and adaptive capacity. Science of The Total Environment 682, 31-46.
| Crossref | Google Scholar | PubMed |
Nikolić G, Vujović F, Golijanin J, Šiljeg A, Valjarević A (2023) Modelling of wildfire susceptibility in different climate zones in Montenegro using GIS-MCDA. Atmosphere 14(6), 929.
| Crossref | Google Scholar |
Ning L, Peng W, Yu Y, Xiang J, Wang Y (2023) Quantifying vegetation change and driving mechanism analysis in Sichuan from 2000 to 2020. Frontiers in Environmental Science 11, 1261295.
| Crossref | Google Scholar |
Oliveira S, Zêzere JL, Queirós M, Pereira JM (2017) Assessing the social context of wildfire-affected areas. The case of mainland Portugal. Applied Geography 88, 104-117.
| Crossref | Google Scholar |
Oliveira S, Rocha J, Sá A (2021) Wildfire risk modeling. Current Opinion in Environmental Science & Health 23, 100274.
| Crossref | Google Scholar |
Peng W, Kuang T, Tao S (2019) Quantifying influences of natural factors on vegetation NDVI changes based on geographical detector in Sichuan, western China. Journal of Cleaner Production 233, 353-367.
| Crossref | Google Scholar |
Peng W, Wei Y, Chen G, Lu G, Ye Q, Ding R, Hu P, Cheng Z (2023) Analysis of wildfire danger level using logistic regression model in Sichuan Province, China. Forests 14(12), 2352.
| Crossref | Google Scholar |
Phelps N, Woolford DG (2021) Comparing calibrated statistical and machine learning methods for wildland fire occurrence prediction: a case study of human-caused fires in Lac La Biche, Alberta, Canada. International Journal of Wildland Fire 30(11), 850-870.
| Crossref | Google Scholar |
Polat A (2021) An innovative, fast method for landslide susceptibility mapping using GIS-based LSAT toolbox. Environmental Earth Sciences 80(6), 217.
| Crossref | Google Scholar |
Pourghasemi HR (2016) GIS-based forest fire susceptibility mapping in Iran: a comparison between evidential belief function and binary logistic regression models. Scandinavian Journal of Forest Research 31(1), 80-98.
| Crossref | Google Scholar |
Pourtaghi ZS, Pourghasemi HR, Rossi M (2015) Forest fire susceptibility mapping in the Minudasht forests, Golestan province, Iran. Environmental Earth Sciences 73(4), 1515-1533.
| Crossref | Google Scholar |
Qin Y, Zhao Z, Zhou D, Chang K, Mou Q, Yang Y, Hu Y (2024) Landslide susceptibility assessment in Yulong County using Contribution Degree Clustering Method and Stacking Ensemble Coupled Model based on Certainty Factor. Remote Sensing 16(19), 3582.
| Crossref | Google Scholar |
Rihan W, Zhao J, Zhang H, Guo X, Ying H, Deng G, Li H (2019) Wildfires on the Mongolian Plateau: identifying drivers and spatial distributions to predict wildfire probability. Remote Sensing 11(20), 2361.
| Crossref | Google Scholar |
Rivière M, Lenglet J, Noirault A, Pimont F, Dupuy J-L (2023) Mapping territorial vulnerability to wildfires: a participative multi-criteria analysis. Forest Ecology and Management 539, 121014.
| Crossref | Google Scholar |
Salavati G, Saniei E, Ghaderpour E, Hassan QK (2022) Wildfire risk forecasting using weights of evidence and statistical index models. Sustainability 14(7), 3881.
| Crossref | Google Scholar |
Sevgen E, Kocaman S, Nefeslioglu HA, Gokceoglu C (2019) A novel performance assessment approach using photogrammetric techniques for landslide susceptibility mapping with logistic regression, ANN and random forest. Sensors 19(18), 3940.
| Crossref | Google Scholar | PubMed |
Sharma LK, Gupta R, Fatima N (2022) Assessing the predictive efficacy of six machine learning algorithms for the susceptibility of Indian forests to fire. International Journal of Wildland Fire 31(8), 735-758.
| Crossref | Google Scholar |
Sivrikaya F, Küçük Ö (2022) Modeling forest fire risk based on GIS-based analytical hierarchy process and statistical analysis in Mediterranean region. Ecological Informatics 68, 101537.
| Crossref | Google Scholar |
Su L, He Y, Chen S (2015) Temporal and spatial characteristics and risk analysis of forest fires in China from 1950 to 2010. Scientia Silvae Sinicae 51(1), 88-96.
| Google Scholar |
Su Y, Zhao L, Li X, Li H, Ge Y, Chen J (2024) FC-StackGNB: a novel machine learning modeling framework for forest fire risk prediction combining feature crosses and model fusion algorithm. Ecological Indicators 166, 112577.
| Crossref | Google Scholar |
Tavakkoli Piralilou S, Einali G, Ghorbanzadeh O, Nachappa TG, Gholamnia K, Blaschke T, Ghamisi P (2022) A Google Earth Engine approach for wildfire susceptibility prediction fusion with remote sensing data of different spatial resolutions. Remote Sensing 14(3), 672.
| Crossref | Google Scholar |
Tian Y, Wu Z, Li M, Wang B, Zhang X (2022) Forest fire spread monitoring and vegetation dynamics detection based on multi-source remote sensing images. Remote Sensing 14(18), 4431.
| Crossref | Google Scholar |
Tiwari A, Shoab M, Dixit A (2021) GIS-based forest fire susceptibility modeling in Pauri Garhwal, India: a comparative assessment of frequency ratio, analytic hierarchy process and fuzzy modeling techniques. Natural Hazards 105, 1189-1230.
| Crossref | Google Scholar |
Wang W, Fang X, Wei X, Ye J (2024) Optimized stratification approach enhances the weight-of-evidence method: transparently uncovering wildfire probability and drivers-wildfire relationships in the southwest mountains of China. Ecological Indicators 158, 111500.
| Crossref | Google Scholar |
Woinarski JC, McCormack PC, McDonald J, Legge S, Garnett ST, Wintle B, Rumpff L (2023) Making choices: prioritising the protection of biodiversity in wildfires. International Journal of Wildland Fire 32(7), 1031-1038.
| Crossref | Google Scholar |
Wu B, Song Z, Wu Q, Wu J, Yu B (2023) A vegetation nighttime condition index derived from the triangular feature space between nighttime light intensity and vegetation index. IEEE Transactions on Geoscience and Remote Sensing 61, 1-15.
| Crossref | Google Scholar |
Xepapadeas P, Douvis K, Kapsomenakis I, Xepapadeas A, Zerefos C (2024) Assessing the link between wildfires, vulnerability, and climate change: insights from the regions of Greece. Sustainability 16(11), 4822.
| Crossref | Google Scholar |
Xiao Y, Tang X, Li Y, Huang H, An B-W (2022) Social vulnerability assessment of landslide disaster based on improved TOPSIS method: case study of eleven small towns in China. Ecological Indicators 143, 109316.
| Crossref | Google Scholar |
Xing Y, Chen Y, Huang S, Xie W, Wang P, Xiang Y (2023) Research on the uncertainty of landslide susceptibility prediction using various data-driven models and attribute interval division. Remote Sensing 15(8), 2149.
| Crossref | Google Scholar |
Xiong Q, Luo X, Liang P, Xiao Y, Xiao Q, Sun H, Pan K, Wang L, Li L, Pang X (2020) Fire from policy, human interventions, or biophysical factors? Temporal–spatial patterns of forest fire in southwestern China. Forest Ecology and Management 474, 118381.
| Crossref | Google Scholar |
Yang X, Jin X, Zhou Y (2021) Wildfire risk assessment and zoning by integrating Maxent and GIS in Hunan province, China. Forests 12(10), 1299.
| Crossref | Google Scholar |
Yue W, Ren C, Liang Y, Liang J, Lin X, Yin A, Wei Z (2023) Assessment of wildfire susceptibility and wildfire threats to ecological environment and urban development based on GIS and multi-source data: a case study of Guilin, China. Remote Sensing 15(10), 2659.
| Crossref | Google Scholar |
Zhang G, Wang M, Liu K (2021) Deep neural networks for global wildfire susceptibility modelling. Ecological Indicators 127, 107735.
| Crossref | Google Scholar |