Towards benchmarking the dynamically downscaled CMIP6 CORDEX-Australasia ensemble over Australia
Xiaoxuan Jiang A B C , Emma Howard D * , Chun-Hsu Su
A B C , Emma Howard D * , Chun-Hsu Su  E , Rachael N. Isphording F G , Benjamin Ng H , Sarah Chapman
E , Rachael N. Isphording F G , Benjamin Ng H , Sarah Chapman  I J , Fei Ji K , Michael Grose
I J , Fei Ji K , Michael Grose  L , Jozef Syktus
L , Jozef Syktus  J , Ralph Trancoso I J , Marcus Thatcher H , Sugata Narsey
J , Ralph Trancoso I J , Marcus Thatcher H , Sugata Narsey  E , Giovanni Di Virgilio F K and Jatin Kala M
E , Giovanni Di Virgilio F K and Jatin Kala M
A
B
C
D
E
F
G
H
I
J
K
L
M
Handling Editor: Peter May
Abstract
This study applies a benchmarking framework to assess a 34-member ensemble of regional climate models that have dynamically downscaled Coordinated Model Intercomparison Project (CMIP6) models over the Australasian region. Four modelling centres contributed regional climate models to this ensemble using three regional climate models (RCMs) and a total of five model configurations. The RCMs compared are the Conformal Cubic Atmospheric Model (CCAM), the Weather Research and Forecast (WRF) model and the Bureau Atmospheric Regional Projections for Australia (BARPA-R). Assessment is conducted over the Australian continent using a separation into four major climate zones over a 30-year historical climatological period (1985–2014). Rainfall and near-surface temperatures are compared against six benchmarks measuring mean state patterns, spatial and temporal variance, seasonal cycles, long-term trends and selected extreme indices. Benchmark thresholds are derived either from previous studies or comparison with the driving model ensemble. Major model biases vary between ensemble members and include dry biases in northern and southern Australia, winter wet biases and a persistent low bias in the winter diurnal temperature range across all the modelling centres. Daily variability at large length scales is comparable in the driving global climate model and downscaled regional climate model length scales, and long-term trends are largely determined by the driving global climate model. Overall, the ensemble was deemed to be fit for purpose for impact studies. Strengths and weaknesses of the systematic benchmarking framework used here are discussed.
Keywords: Australian climate, benchmarking, CORDEX-Australasia, CORDEX-CMIP6, model evaluation, rainfall, regional climate models, regional climate projections, temperature.
1.Introduction
Regional climate model (RCM) projections are an invaluable tool for preparing for the impacts of climate change on local communities and ecosystems (Giorgi 2019). Climate risk assessments require regional-scale information to generate projections of future climate hazards. Most global climate projections are generated by coarse-resolution general circulation models (GCMs), which are not designed to sufficiently resolve regional-scale processes and geographical features that have key influences on regional climate (e.g. Munday and Washington 2018). Therefore, regional downscaling of GCMs is necessary to produce climate hazard projections at length scales that are most relevant for planning and policy-making purposes.
1.1. CORDEX downscaling
The Coordinated Regional Downscaling Experiment (CORDEX) is a powerful framework that coordinates the creation and comparison of ensembles of RCM simulations (Gutowski et al. 2016). Ensemble methods are vital in the production of RCM projections owing to the considerable uncertainties associated with the regional manifestation of anthropogenic climate change, particularly with regard to rainfall change and the water cycle. This is especially the case in the Australian region, where natural climate variability is already extremely high (e.g. Nicholls et al. 1997). CORDEX is the regional counterpart of the Coupled Model Intercomparison Project (CMIP), currently in its sixth phase (Eyring et al. 2016).
Through the first phase of CORDEX, downscaled climate simulations were produced for 14 continental-scale regions. In the Australasian region, five modelling centres participated in dynamically downscaling CMIP5 projections over Australia, New Zealand and the western Pacific (Evans et al. 2021). A total of 24 GCM–RCM dynamically downscaled pairs were produced (Isphording et al. 2024a). The CORDEX-Australasian ensemble (CORDEX-CORE) was also used in the Intergovernmental Panel on Climate Change Sixth Assessment Report (IPCC AR6) in their assessment of regional changes through the AR6 Atlas (Giorgi et al. 2021; Gutiérrez et al. 2021). Statistical downscaled projections were produced for 22 GCMs by the Bureau of Meteorology in the National Hydrological Projections (NHP) project (Wilson et al. 2022); this ensemble was used to underpin the Bureau of Meteorology’s Australian Water Outlook service. These experiments have formed the basis of state and federal climate assessments such as the 2019 Victorian Climate Projections (Clarke et al. 2019) and the Energy Sector Climate Information Project (CSIRO et al. 2021).
More recently, Australian modelling centres have commenced the downscaling of CMIP6 models to the CORDEX-Australasian domain, and this will form a core resource for new national projections (Grose et al. 2023). This effort involves four modelling centres, three independent RCMs and five RCM configurations. Two RCMs were run through the Australian Climate Service (ACS) and two by the state governments of New South Wales and Queensland. For clarity, in this paper we distinguish between the terminology ‘RCM’ to describe each model configuration or downscaling methodology, ‘RCM simulation’ to describe a single downscaling of a GCM by a RCM and ‘RCM ensemble’ to refer to the full set of RCM simulations.
1.2. RCM evaluation
To assist users in effectively using dynamically downscaled data to study the different impacts of climate change, it is informative to assess the capacity of RCMs to produce credible or physically plausible simulations of future climate. This traditionally relies on a rule of thumb, where the ability to sufficiently represent the observed climate is used as a prerequisite for being considered in projections and part of the evidence used to assign confidence in projections. To achieve this evaluation, downscaled simulations of CMIP Tier-1 Historical experiments, which use contemporary levels of radiative forcing, are assessed against corresponding contemporary climate observations in order to assess the skill of RCMs at simulating recent climate.
Cross-ensemble evaluation studies enhance the congruency of RCM data by enabling users to assess the performance of multiple potential data sources at once. To this effect, Vautard et al. (2021) carried out a comprehensive cross-ensemble evaluation of the EURO-CORDEX ensemble, assessing mean-state biases and the representation of extremes in a set of climate and impact-based variables. Particular focus was given to surface temperatures, rainfall and the water cycle. Evans et al. (2021) assessed monthly and annual biases, root mean square errors (RMSEs) and spatial correlations of temperatures and precipitation in CORDEX-Australasia Phase 1, downscaling CMIP5. They identified systematic biases common to most models in the ensemble, including underestimated diurnal temperature ranges and southern Australian rainfall. Meyer et al. (2021) assessed precipitation within the North American CORDEX ensemble, with a particular focus on seasonality. An extension into process-based evaluation, such as the evaluation of atmospheric processes and pressure patterns associated with synoptic systems (e.g. Pinto et al. 2018) provides further insight into RCM simulation performance, particularly in data-sparse regions such as southern Africa.
1.3. From evaluation to benchmarking
The Australian CORDEX-CMIP6 RCMs have been evaluated individually using different evaluation approaches. Chapman et al. (2023) found that downscaling CMIP6 models with the Conformal Cubic Atmospheric Model (CCAM) led to improvements mainly in coastal and mountainous regions and for extremes when compared with the host GCM. Howard et al. (2024) presented the Bureau of Meteorology Regional Projections for Australia (BARPA-ACS), a RCM that is contributing downscaled GCMs to CORDEX-Australasia for the first time under CORDEX-CMIP6. BARPA-ACS is based on the same modelling components used by the Bureau of Meteorology for weather and seasonal predictions and by the UK Met Office for global and regional projections. Schroeter et al. (2024) assessed the ERA-5 downscaling of CCAM-ACS. Di Virgilio et al. (2025a) evaluated ERA5-driven NARCliM2.0 (NSW and Australian Regional Climate Modelling) simulations for mean climate, attributing improvements in the simulation of precipitation principally to the driving ERA5 and improvements in maximum temperature principally to RCM design choices. Ji et al. (2024) evaluated ERA5-driven NARCliM2.0 simulations for precipitation extremes, reporting that RCMs captured climatology and the coefficient of variation of precipitation extremes well but struggled with temporal correlation and trends. Di Virgilio et al. (2025b) further assessed CMIP6 GCM-driven NARCliM2.0 simulations, finding much smaller biases in maximum temperature and reduced wet biases compared with NARCliM1.0 and 1.5, though with minimal improvement in minimum temperature. Further details of the participating CORDEX-Australasia RCMs are provided in Section 2 below.
There are two major caveats to traditional evaluation methodologies when considering CORDEX simulations. The first is that RCM simulations are reliant on a host model, so evaluation of both the host model simulation and the RCM simulation is needed to get a complete picture, with RCM simulation evaluation giving insights only into the stage in the process that it plays. The second is the lack of objective thresholds for establishing reasonable performance or for informing confidence in projections. Historically, a set of various evaluation metrics have been produced (often not comprehensive or objectively selected), and then the fitness for purpose of a model estimated using expert judgment. However, there are advantages in moving to a more transparent, quantitative and systematic framework, hence the call for attempting a ‘benchmarking’ approach rather than ad hoc or subjective evaluation. Although benchmarking aims to improve the objectivity of model evaluation, some degree of subjectivity cannot be entirely eliminated and remains in the choice of benchmarked metrics and thresholds.
1.4. Benchmarking
Within the Earth Sciences, the land-surface modelling community has led the adoption of benchmarking model evaluation frameworks (e.g. Abramowitz et al. 2005, 2012). The development of the ‘ILAMB’ (International Land Model Benchmarking) model evaluation tool (Collier et al. 2018) is an example of this, providing a standard computational framework to compare model data. ILAMB provides a flexible framework to assess any two-dimensional model against a corresponding observational data set, comparing biases, seasonal peaks, RMSEs and spatial correlations. Other tools, such as ESM-Val-Tool (Eyring et al. 2020), have a wide uptake in the CMIP global modelling community. Benchmarks can be used to measure generational model improvements (Alexander and Arblaster 2009, 2017; Flato et al. 2013; Sillmann et al. 2013; Fiedler et al. 2020), with increased spatial resolution (Bador et al. 2020; Nishant et al. 2022) and to assess the benefits and degradations associated with particular parameterisations, experimental designs, or GCM–RCM combinations (Ji et al. 2014; Liu et al. 2024). The value of moving from evaluation to benchmarking has been recognised for selecting CMIP models fit for downscaling (Nguyen et al. 2024) and in Extreme Event Attribution applications (Grose et al. 2023).
A particular focus on benchmarking precipitation has emerged in recent years (Ahn et al. 2022, 2023; Martinez-Villalobos et al. 2022). United States Department of Energy (2020) provided a seminal guidance document, which Isphording et al. (2024a) have adapted into a two-tier set of objectively defined benchmarks. The first tier of benchmarks seeks to establish a ‘minimum standard’ in model performance, defining metrics to assess rainfall bias, spatial distribution, seasonal cycle and long-term trends. The second tier of versatility metrics can provide a deeper understanding of temporal variability, distributions, extremes and drought.
1.5. Objectives of this study
This paper presents the first study applying a standardised evaluation and benchmarking approach across the CORDEX-Australasia CMIP6 ensemble. It combines the ILAMB and Isphording et al. (2024a) methodologies to benchmark precipitation and near-surface temperatures for the CORDEX-Australasia downscaling of CMIP6. We assess aggregated bias, spatial patterns, the seasonal cycle, temporal distributions, long-term trends and extreme indices using benchmarks drawn from Isphording et al. (2024a) where possible, and the CMIP6 ensemble mean in other cases. The specific thresholds from Isphording et al. (2024a) are used for inter-comparability, except some modifications and extra discussion are added, particularly for trends. These assessed quantities have been informed by the ILAMB project, and an ILAMB dashboard is provided as a supplementary resource. In order to ensure compatibility with the ILAMB framework, some minor adjustments have been made to the minimum standard metrics defined in Isphording et al. (2024a). Namely, spatial mean absolute percentage errors have been replaced with a centred root mean squared error (cRMSE) in order to facilitate display on a Taylor diagram and aggregated bias metrics have been included.
This study provides an exploratory view on the use of systematic benchmarking ahead of more subjective evaluation in a comparative analysis of a multi-GCM, multi-RCM climate downscaling ensemble. Rather than simply presenting a binary perspective, care has been taken to ensure that the underlying quantitative performance is provided for each metric. Our interpretation of benchmarks is as an outside reference point of good model performance, rather than as a hard binary to exclude models. Model climatology assessments can sometimes present bias maps as a routine component of evaluation; however, the choice of colour limit bounds can easily distort reader perception of bias magnitude, and a reference benchmark can aid in avoiding this. Some benchmarks, such as the extreme index benchmarks, are defined to be ambitious. Performance against a single benchmark should not be taken as a reason to reject a model out of hand. Rather, the benchmarks should be considered in concert with each other, and interpreted through the lens of each user application. This approach highlights the strengths and weaknesses of different models. The results from the benchmarking can also inform the needs and strategies for further processing of the modelling data to generate application-specific data. For example, benchmarking may inform the selection of models for developing contrasting storyline-based analysis, or the degree of bias correction deemed necessary before RCM simulation data can be used for impact-modelling applications.
This paper proceeds as follows. Section 2 describes the three different RCM designs that are benchmarked in this work for their simulated surface air temperature and precipitation over four Australian climate zones. The benchmarking methodologies in terms of regions, aggregation strategies and definitions of benchmarks, are also described. Section 3 presents an analysis of the observational uncertainty present in the benchmark values. Section 4 describes the benchmarks and benchmarking performance in the mean state, focussing on mean state characteristics of the RCM simulations, including biases, spatial patterns, seasonal cycles, temporal distributions and long-term trends. This is followed by Section 5, which benchmarks the RCMs with climate indicators that focus on wet precipitation and hot temperature extremes. Section 6 discusses the overall results and concludes the paper.
2.Methods
2.1. Models
This paper presents one approach to benchmark-based assessment of the RCM ensemble generated by four Australian regional climate modelling groups for CORDEX-CMIP6. These groups have participated in dynamical downscaling of CMIP6 projections for the Australasian region using three independent RCMs and five distinct model configurations. GCM selection followed a co-ordinated ‘sparse matrix’ approach to facilitate overlap in the selected GCMs and test the uncertainty in climate projections to RCM configuration. The model selection process is documented by Chapman et al. (2023), Grose et al. (2023) and Di Virgilio et al. (2022). Table 2 presents the sparse matrix of selected GCM–RCM simulation combinations.
The CCAM is a variable resolution global climate model (VR-GCM), possessing more freedom in its use as a downscaling model compared with the more traditional limited area models (LAMs). CCAM has been used in two separate configurations by two different modelling groups: the Queensland Future Climate Science Program (QFCSP; collaboration between the University of Queensland and the Queensland Government), producing QldFCP-2 (Queensland Future Climate Projections 2), and the Australian CSIRO in partnership with the Australian Climate Service (ACS) producing CCAM-ACS. CCAM uses the Community Atmosphere Biosphere Land Exchange (CABLE).
The CSIRO-ACS configuration of CCAM uses a C384 grid with a high-resolution region of 12.5 km. The model employs 54 vertical levels between 20 m and 40 km in the atmosphere and 40 levels in the ocean (to a depth of 5 km). To constrain the model when downscaling an ensemble of GCMs, CCAM uses a spectral nudging approach (Thatcher and McGregor 2009). Winds, air temperature and surface pressure are nudged approximately a length scale of 3000 km and above 850 hPa. Water vapour is not nudged, but allowed to evolve by the atmosphere model’s dynamics and physics. This is to avoid accidently preventing or duplicating precipitation events if the timing of rainfall differs between the regional model and the host GCM. CCAM has a coupled configuration for improving sea surface temperatures (SSTs) in the vicinity of coastlines (Thatcher et al. 2015), but with spectral nudging to ensure SSTs agree with the host GCM at a length scale of 1000 km. This approach to downscaling ensures that CCAM is reasonably constrained to follow the host GCM, but it will also inherit large scale biases and errors from the GCM.
The QldFCP-2 configuration of CCAM is a C288 stretched grid with a high-resolution region of 10 km. The model deploys 35 vertical levels and 30 levels in the ocean. QldFCP-2 uses bias and variance corrected SSTs and sea ice, as documented by Hoffman et al. (2016) and Chapman et al. (2023) and Atmospheric Model Intercomparison Project (AMIP)-style integrations (Gates 1992; Haarsma et al. 2016). In addition the CMIP6 radiative forcings, which consist of time-varying solar forcing, greenhouse gases (CO2, N2O, CH4, chlorofluorocarbons, CFCs), ozone change, aerosols (sulfate, organic, black carbon, dust, volcanic, dimethylsulfide) and transient land cover change were used. Five simulations were also run in ocean-coupled mode, with bias-corrected SSTs with spectral nudging to ensure SSTs agreed with the host GCM at a length scale of 1000 km (see Table 1). However, in order to restrict realisation to one per GCM–RCM pair and to compare like with like, the ocean-coupled QldFCP-2 simulations are not directly assessed by this study. Using this experimental set-up allowed downscaling additional CMIP6 models that did not provide high frequency data for downscaling with a traditional RCM (Thatcher et al. 2015). Both the CCAM-ACS and CCAM-QldFCP-2 have similar configurations for atmosphere, ocean, land surface and aerosol parameterisation. Hence, the differences in the projections arise mostly from the downscaling experiment design (i.e. nudged v. bias-corrected) and some differences in the horizontal and vertical resolution and stretching.
| CMIP6 GCM | QldFCP-2 | NARCliM2.0 | CCAM-ACS | BARPA-ACS | CMIP6 missing data | |
|---|---|---|---|---|---|---|
| ACCESS CM2 | r2i1p1f1 (oc) | r4i1p1f1 | r4i1p1f1 | |||
| ACCESS ESM1.5 | r6i1p1f1 | 2*(r6i1p1f1) | r6i1p1f1 | r6i1p1f1 | ||
| r20i1p1f1 (oc) | ||||||
| r40i1p1f1 (oc) | ||||||
| CESM2 | r11i1p1f1 | r11i1p1f1 | Tasmax, tasmin | |||
| CMCC-ESM2 | r1i1p1f1 | r1i1p1f1 | r1i1p1f1 | |||
| CNRM-CM6.1-HR | r1i1p1f2 | |||||
| r1i1p1f2 (oc) | ||||||
| CNRM-ESM2-1 | r1i1p1f2 | |||||
| EC-Earth3 | r1i1p1f1 | r1i1p1f1 | r1i1p1f1 | |||
| EC-Earth3-Veg | 2*(r1i1p1f1) | |||||
| FGOALS-g3 | r4i1p1f1 | |||||
| GFDL-ESM4 | r1i1p1f1 | |||||
| GISS-E2-1-G | r2i1p1f2 | Daily precipitation | ||||
| MPI-ESM1-2-HR | 2*(r1i1p1f1) | r1i1p1f1 | ||||
| MPI-ESM1-2-LR | r9i1p1f1 | |||||
| MRI-ESM2-0 | r1i1p1f1 | |||||
| NorESM2-MM | r1i1p1f1 | 2*(r1i1p1f1) | r1i1p1f1 | r1i1p1f1 | ||
| r1i1p1f1 (oc) | ||||||
| UKESM1-0-LL | 2*(r1i1p1f2) |
This table includes the QldFCP-2 ocean-coupled simulations, labelled ‘oc’, that are not directly assessed in this paper. Table entries indicate the CMIP6 variant ID of the selected driving experiment, following Chapman et al. (2023), Grose et al. (2023) and Di Virgilio et al. (2022).
BARPA-ACS refers to the Bureau of Meteorology moderate-scale climate downscaling model based on uses the UK Met Office Unified Model for modelling the atmosphere and Joint UK Land Environment Simulator (JULES) for the land surface. These are the same modelling components used by the Bureau for weather and seasonal predictions and reanalysis, and by the UK Met Office for global and regional projections. Set up with a horizontal regular latitude–longitude grid spacing of 0.1545°, it is configured with the global atmosphere and land (GAL) physics configuration HadREM3-GA7-05 (Walters et al. 2019; Tucker et al. 2022) with additional changes to improve land surface characterisation, grid point storms and convection (Su et al. 2022). The model top is either 41 km across 64 vertical levels, or 32 km across 61 vertical levels, depending on the height of available global model data. The former vertical level set is used with all but CESM2, CMCC-ESM2 and NorESM2-MM experiments. The model is forced at the lateral boundary and SST data from global models. It is also dynamically nudged towards global fields of temperature and winds between 11 and 37 km above the surface.
NARCliM provides high-resolution climate projections for CORDEX-Australasia and south-eastern Australia at different resolutions tailored to the specific needs of the regions. To date, NARCliM has completed three major phases: the first generation of NARCliM(1.0) was delivered in 2014 (Evans et al. 2014), the second generation of NARCliM(1.5) was delivered in 2020 (Nishant et al. 2021) and the third generation of NARCliM(2.0) was delivered in 2024 (Di Virgilio et al. 2025b). These NARCliM projects downscaled GCM outputs from the CMIP Phases 3, 5 and 6 (CMIP3, CMIP5 and CMIP6). NARCliM2.0 comprises of two Weather Research and Forecasting (WRF) version 4.1.2 (Skamarock et al. 2019) RCMs downscaling five CMIP6 global climate models contributing to CORDEX-Australasia at 20-km resolution, and south-east Australia at 4-km convection-permitting resolution (Di Virgilio et al. 2025b). The two RCMs (R3 and R5) were selected from 78 combinations of physics parameterisations in WRF based on their performance in simulating the recent Australian climate and statistical independence. The five GCMs were shortlisted from the CMIP6 ensemble considering their performance, statistical independence and possible future changes (Di Virgilio et al. 2022). Evaluations and comparison of reanalysis and GCM-driven simulations across three generations of NARCliM indicate that NARCliM2.0 significantly reduced biases in maximum temperature and precipitation, particularly in south-east Australia, making it more reliable for climate-impact assessments and future planning (Ji et al. 2024; Di Virgilio et al. 2025b). These improvements are primarily due to advancements in the RCMs (Di Virgilio et al. 2025b). The model configurations for BARPA-ACS, CCAM-ACS, QldFCP-2 and NARCliM2.0 are summarised in Table 2.
| Name | Institute | Horizontal grid spacing (°) | Description | |
|---|---|---|---|---|
| BARPA-ACS | Bureau of Meteorology | 0.1545 | Met Office Unified Model coupled to JULES land surface model: limited area domain. Global Atmosphere 7 configuration with fountain buster and Global Atmosphere 8 convection parameterisation scheme. GCM provides lateral and SST boundary conditions. Dynamical atmospheric nudging of winds and temperatures to driving GCM from 11 km and above (Su et al. 2022; Howard et al. 2024) | |
| CCAM-ACS | CSIRO | 0.11 | CCAM with CABLE land surface model and inline ocean model. Global stretch-grid model with spectral atmospheric nudging of winds and temperatures to driving GCM (Schroeter et al. 2024) | |
| CCAM-QldFCP-2 | The University of Queensland and Department of Energy and Climate, Queensland | 0.11 | CCAM with CABLE land surface model and inline ocean model. Free-running global stretch-grid model with bias-corrected SSTs and CMIP6 radiative forcings as the source of driving data (Chapman et al. 2023) | |
| NARCliM2-0-WRF412R3 | Department of Climate Change, Energy, the Environment and Water, New South Wales | 0.18 | WRF Model Version 4.1.2 with MYNN2 planetary boundary layer, Thompson microphysics, BMJ cumulus physics, RRTMG shortwave and longwave radiation physics and Noah-multiparametrisation land surface model with dynamic vegetation option. Limited area domain (Di Virgilio et al. 2025b) | |
| NARCliM2-0-WRF412R5 | Department of Climate Change, Energy, the Environment and Water, New South Wales | 0.18 | WRF Model Version 4.1.2 with ACM2 planetary boundary layer, Thompson microphysics, BMJ cumulus physics, RRTMG shortwave and longwave radiation physics and Noah-multiparametrisation land surface model with dynamic vegetation option. Limited area domain (Di Virgilio et al. 2025b) |
Abbreviations are as follows: CCAM, Conformal Cubic Atmospheric Model; MYNN, Mellor–Yamada–Nakanishi–Niino; BMJ:, Betts–Miller–Janjic; RRTMG, Rapid Radiative Transfer Model for GCM applications; WRF, Weather Research and Forecasting.
2.2. Data
The core climatological period considered for this work is 1985–2014, the last 30 years of the CORDEX historical time period. For long-term trend analysis (Section 4.5), this time period is extended to 1960–2014, which is the maximum overlapping time period available from all RCM simulations considered.
The Australian Gridded Climate Data (AGCD) Version 1 provides a gridded daily 0.05 × 0.05° analysis of station daily maximum and minimum 2 m (screen-level) temperature data, and daily precipitation accumulation (Jones et al. 2009). For brevity, these temperatures are referred to as tasmax and tasmin, and precipitation as pr. This study used CSIRO’s commercially licensed version of the Bureau of Meteorology’s AGCD data set (see https://doi.org/10.25914/6009600304b02), which is accessible through the National Computing Infrastructure. For more information on this version, please refer to https://github.com/AusClimateService/agcd-csiro. The AGCD grids are generated using an optimised Barnes successive-correction method that applies weighted averaging to the station data. Topographical information is included by using anomalies from long-term (monthly) averages in the analysis process. The AGCD analysis errors for tasmax are larger near the coast around north-west Australia and around the Nullarbor Plain owing to strong temperature gradients between the coast and inland deserts and a sparse observational network (Jones et al. 2009). The coast of Western Australia and parts of the Northern Territory are likely to share this analysis issue. The analysis errors are larger for tasmin, especially over Western Australia and the Nullarbor Plain. For precipitation, the rain gauge analysis of daily accumulation over Australia was produced using the Barnes method in which the ratio of observed rainfall to monthly average is used in the analysis process (Jones et al. 2009). There is a north–south gradient in the AGCD analysis errors, with larger analysis errors in the northern tropical regions, where the length scales of rainfall events are shorter and more convective. A spatial mask is applied to all precipitation fields to exclude regions where station influence is low; the excluded region is shown in grey in Fig. 1.
Cluster masks for NRM superclusters and subclusters used in this study, following Clarke et al. (2015). The precipitation data mask is shown in grey.

Spatial aggregation is performed using four Australian climate zones, known as the National Resource Management (NRM) superclusters (Clarke et al. 2015). These supercluster regions are shown with filled colours in Fig. 1. As well as following the boundaries of Australia’s NRM regions, these superclusters are climatologically distinct and represent the four major climate zones of Australia. The four NRM superclusters were favoured over the 8 NRM clusters and the 15 NRM subclusters owing to the large quantity of models being analysed in this paper. Superclusters were judged to reduce the quantity of results to an acceptable level while still separating these four most distinct climates in Australia. The four clusters approximately correspond to tropical (northern Australia), subtropical (eastern Australia), temperate (southern Australia) and arid climates (rangelands). The accompanying ILAMB dashboard includes a further breakdown of the assessment into eight clusters for increased granularity, and also includes spatial maps. However, as observed rainfall trends considered in Section 4.5 are localised, three NRM subclusters with well-studied trends have been selected as case studies. These regions are indicated with outlines in Fig. 1.
Climate indices are calculated metrics used to represent the state of the climate system and its changes. In this study, the open-source Python library ICCLIM (Index Calculation for CLIMate) Version 6.5.0 (Pagé et al. 2022, Aoun et al. 2024) is used to calculate the following monthly indices: maximum 1-day total precipitation (RX1day), average precipitation during wet days (SDII), number of wet days when precipitation is greater than or equal to 1 mm (RR1), maximum consecutive wet days when precipitation is greater than or equal to 1 mm (CWD), maximum consecutive dry days when precipitation is less than 1 mm (CDD), maximum daily maximum temperature (TXx) and maximum daily minimum temperature (TNx). These indices were chosen to capture heavy precipitation and hot temperature extremes over Australia and are calculated using daily precipitation, tasmax and tasmin. Indices computed using ICCLIM definitions provided by the European Climate Assessment & Dataset with detailed descriptions and the equations of individual indices can be found in the Algorithm Theoretical Basis Document (ATDB; Royal Netherlands Meteorological Institute 2021).
2.3. Methodology
This benchmarking assessment focuses on two atmospheric variables: near-surface temperature and precipitation, divided into three core and six additional indices. The reference observational data set used throughout this study is the AGCD (Section 2.2). As such, the present study is an attempt at benchmarking the statistics of the diagnosed variables of interest, not of processes underpinning the simulation of these variables (although the concept has value for this too; see Discussion).
The observed and modelled core variables (tasmax, tasmin and daily precipitation) are aggregated to monthly means and assessed in Section 4. The assessment for the ICCLIM indices is presented in Section 5. For each core variable, benchmarks are applied to assess model biases, spatial distributions, temporal distributions, seasonal cycles and long-term trends. The ICCLIM indices are benchmarked by their seasonal mean absolute errors (MAEs). A summary of each benchmark is provided in Table 3, and the flow chart shown in Fig. 2 illustrates the computational method for each benchmark. The description of each benchmark in Sections 4 and 5 is split into a ‘benchmark description’ subsection that describes the rationale and computation method for each benchmark, and a ‘benchmark performance’ subsection that discusses the performance of the RCM ensemble at meeting the benchmark.
| Variable | Metric | Benchmark | Spatial aggregation | Temporal aggregation | |
|---|---|---|---|---|---|
| Core: tasmax, tasmin, precipitation | Bias | Mean absolute bias averaged over the ensemble of CMIP6 downscaled model | NRM supercluster | Climatological season | |
| Spatial pattern | Fixed thresholds (not GCMs): cNRMSE < 0.65, spatial correlation >0.7 | Native grid | Climatological season | ||
| Seasonal cycle | Fixed thresholds (not GCMs): correct timing of months with the highest and lowest values | NRM supercluster | Climatological month | ||
| Unbiased temporal distribution of daily data | Ensemble mean of unbiased distribution alignment taken from driving GCM ensemble (bins: 0.2 mm or 0.2°C) | NRM supercluster | Daily | ||
| tasmax/tasmin long-term trend | Confidence intervals of Thiel–Sen slope estimator overlap at a P = 0.05 level | NRM super-cluster | Annual | ||
| Precipitation long-term trend | Select NRM subclusters | Seasonal | |||
| ICCLIM | Precipitation index MAPE | Seasonal MAPE of CMIP6 ensemble on 1.5° grid for RR1, RX1Day, SDII, CWD, CDD | NRM supercluster | Climatological season | |
| Temperature index MAE | Seasonal MAE of CMIP6 ensemble on 1.5° grid for TXx, TNx |
The three core variables are daily maximum (tasmax) and minimum (tasmin) near-surface temperature and daily precipitation. ICCLIM indices are abbreviated as per Section 2.2. cNRMSE refers to normalised and unbiased root mean square error, MAPE to mean absolute percentage error and MAE to mean absolute error.
Flow chart of computation methodologies for applied benchmarks. Coloured boxes indicate time means (green), spatial means (pink), benchmark threshold definitions (blue), benchmarked metrics (purple) and benchmark definitions (orange).

We use a weighted mean approach to aggregate the core variables from their local grids to NRM superclusters, where weights derive from the fractional overlap between each model grid cell and each NRM supercluster. Benchmarking of spatial patterns is performed on each model’s native grid by upscaling observational data to the model grid.
In order to define meaningful measures of performance, the bias and temporal distribution analyses both benchmarks against the CMIP6 historical experiment. These benchmarks are defined taking an ensemble mean of CMIP6 GCM performance across all models listed in Table 1 for which the required data were available. Column 6 of Table 1 indicates where GCMs have been excluded from the ensemble mean owing to data availability issues. Each GCM is given equal weighting in the ensemble mean, regardless of how many times it was downscaled. This ensures that the same benchmark values are applied to each RCM simulation, independently of the performance of its individual host model. To generate benchmark thresholds for ICCLIM indices, daily GCM and AGCD data are both conservatively regridded to a common 1.5° grid before computation of the indices. Thresholds for benchmarking were developed from principles of regional downscaling or taken from Isphording et al. (2024a).
3.Observational uncertainty
This paper relies heavily on benchmarking against a single observational data set, which leaves it open to influence from observational uncertainty. To offset this, Table 4 provides an estimate of the observational uncertainty in the studied benchmarks by applying the benchmarking metrics to independent data sources. For the purposes of this study, observational uncertainty is quantified as the difference in the representation of benchmarked metrics between independent observational data sets. Precipitation observational uncertainty is approximated by comparing AGCD with GPM-IMERG V07B (Huffman et al. 2018) for the time period 2001–2020, whereas observational uncertainty in temperature metrics is quantified through comparison with CRU-TS4.02 (Harris and Jones 2019). As GPM-IMERG is a satellite-based product and AGCD is a gauge-based product, the independence of these products is expected to be fairly robust. Observational uncertainty in the precipitation trend, daily temperature distribution and extreme temperature index benchmarks has not been quantified, owing to the short time period of the GPM-IMERG data set and the lack of daily data from CRU-TS4.02.
| Variables | Northern Australia | Eastern Australia | Southern Australia | Rangelands | ||
|---|---|---|---|---|---|---|
| Aggregated bias DJF | Pr (%) | −2.2% (23%) | −1.7% (24%) | −0.7% (26%) | −5.8% (38%) | |
| tasmax (°C) | 0.04 (1.32) | 0.17 (1.04) | 0.22 (0.90) | 0.16 (0.93) | ||
| tasmin (°C) | 0.03 (1.42) | −0.06 (1.99) | 0.01 (2.71) | 0.08 (1.94) | ||
| Aggregated bias JJA | Pr (%) | 26.3% (44%) | −2.1% (28%) | 5.1% (18%) | −3.1% (40%) | |
| tasmax (°C) | −0.003 (1.47) | 0.108 (1.67) | −0.032 (1.27) | 0.091 (1.31) | ||
| tasmin (°C) | −0.25 (2.74) | −0.22 (2.73) | −0.09 (2.25) | −0.155 (2.00) | ||
| Spatial correlation* | Pr | 0.93 (0.7*) | ||||
| tasmax | 0.99 (0.7*) | |||||
| tasmin | 0.99 (0.7*) | |||||
| cNRMSE | Pr | 0.39 (0.65) | ||||
| tasmax | 0.14 (0.65) | |||||
| tasmin | 0.15 (0.65) | |||||
| Temporal distribution scores (DJF)* | Pr | 0.89 (0.77*) | 0.82 (0.64*) | 0.92 (0.69*) | 0.90 (0.73*) | |
| Temporal distribution scores (JJA)* | Pr | 0.95 (0.66*) | 0.87 (0.51*) | 0.84 (>0.80*) | 0.98 (0.65*) | |
| MAPE | RR (%) | 6% (24%) | 9% (31%) | 11% (20%) | 6% (30%) | |
| RX1day (%) | 11% (26%) | 11% (22%) | 15% (19%) | 10% (15%) | ||
| CWD (%) | 12% (36%) | 14% (30%) | 22% (15%) | 8% (24%) | ||
| CDD (%) | 10% (27%) | 9% (35%) | 12% (30%) | 9% (23%) | ||
| SDII | 9% (12%) | 11% (13%) | 20% (12%) | 10% (9%) |
These estimates represent the difference between observational data sets in benchmarked metrics obtained by comparing AGCD with GPM-IMERG and CRU-TS4.02. The benchmark thresholds applied in Sections 4 and 5 are provided in parentheses for reference. Benchmarks that are applied as lower thresholds are indicated with an asterisk (*); all other benchmarks are upper thresholds. Cases where the alternative observation source would not pass the benchmark are indicated in bold. Pr, precipitation
Rows 2–7 of Table 4 show the bias uncertainty, measured as the seasonal aggregated differences between AGCD and GPM-IMERG or CRU-TS4.02. The benchmark value computed from the CMIP6 downscaled ensemble is presented in the table in parentheses for comparison. In most cases, the observational uncertainty is small compared with the benchmark, ranging from 0.2 to 10% of the benchmark value. DJF maximum temperatures form an exception to this, with ratios closer to 20%. However, the largest differences arise in the northern Australian and rangelands dry season precipitation, with observational uncertainties reaching 60 and 26% of the benchmark values in these regions. Therefore, as noted in Section 4.1, these biases are highly uncertain and benchmarking based on dry season rainfall should be interpreted with caution.
The uncertainty in the spatial correlation and spatial cNRMSE benchmarks is presented in the third and fourth sections of Table 4. Uncertainties for temperatures are low, with more variability between GPM-IMERG and AGCDv1 present. The cNRMSE for precipitation is quite high, suggesting a strong role of noise in the fields. Temporal distribution score observational uncertainty accounts for approximately half the benchmark value during DJF.
Finally, the observation uncertainty in the ICCLIM-based precipitation indices is much higher than that of the biases, suggesting that much more uncertainty is present in these extreme indices. Uncertainty is highest in southern Australia. In most other regions and for the first four indices, uncertainties range from 20 to 60% of the benchmark values. SDII also shows particularly high observational uncertainties. The observational uncertainty is also higher than the benchmark for CWD in southern Australia and SDII in both southern Australia and SDII.
4.Results
4.1. Bias benchmark
The bias benchmark compares the magnitude of the large-scale land-based mean-state biases of the RCM ensemble across the four super-NCM clusters with the CMIP6 GCM ensemble that is downscaled. This benchmark is based on the expectation that RCMs should not substantially degrade the representation of the climatic mean state at length scales that are well resolved in GCMs. Figure 3 presents the bias benchmarks for the summer and winter seasons and for precipitation, tasmax and tasmin. The benchmark value is taken as the ensemble average of the absolute NRM-aggregated bias for each CMIP6 historical experiment that has been downscaled in CORDEX-Australasia. This benchmark is then applied to the absolute value of the aggregated bias in each RCM simulation. For informative purposes, the sign of the RCM simulation bias is shown in Fig. 3 for reference. However, our analysis focuses on the magnitude of these biases when comparing with benchmarks. Supplementary Fig. S1 provides the breakdown of the benchmark value across the CMIP6 ensemble subset.
Aggregated bias benchmark for each core variable, season and GCM–RCM pair. Colours and numbers indicate the aggregated bias. The benchmark value is given in the top row. Biases larger than the benchmark are marked by purple squares. Lighter colours represent better performance, whereas darker colours indicate worse performance: (a) precipitation, (b) tasmax, (c) tasmin. Precipitation biases are presented as a percentage of the observed seasonal precipitation, whereas temperature biases are presented in degrees Celsius.

This approach extracts large-scale bias by averaging out smaller-scale spatial inhomogeneity. However, because the ensemble mean is taken on absolute values, negative and positive biases across the different GCMs do not cancel each other. This approach has been deemed appropriate because the GCMs and RCM simulations possess very different levels of spatial inhomogeneity owing to their differing resolutions. Additionally, the approach applied here differs from an added value approach, where RCMs are directly compared with their driving models. Here, we attempt to quantify a single base-line level of bias that we would like the RCMs to exceed. This approach does not quantify the reduction in bias associated with the downscaling process, as would be achieved by an added value study.
Across the RCM ensemble, seasons and NRM superclusters, a total of 69% of aggregated precipitation bias benchmarks are met (Fig. 3a). A majority of RCM simulations feature a dry bias in northern Australia during DJF. Biases in QldFCP-2 are generally homogeneous, owing to the use of bias-corrected SSTs, which substantially reduces the magnitude of biases inherited from the driving GCMs. The notable exception to this is QldFCP-2-NorESM2-MM. Downscaling of NorESM2-MM by BARPA, CCAM-ACS and N2.0-R3 also results in substantial winter wet biases in three out of four NRM superclusters. Caution must be exercised when interpreting rainfall benchmarks in northern Australia during the dry season (JJA) owing to a large degree of observational uncertainty, as was discussed in Section 3.
During the northern Australian monsoon in DJF, all but one of the QldFCP-2, BARPA-ACS and NARCliM2.0 simulations show dry biases. For QldFCP-2, BARPA and N2.0-R3, these dry biases are small to moderate, with 7 out of 22 RCM simulations exceeding the benchmark. However, the dry bias is more pronounced in N2.0-R5, with three RCM simulations precipitating only approximately half as much as observed. This result is consistent with the findings of Di Virgilio et al. (2025a), who demonstrated that N2.0-R5 also had a strong monsoon bias when forced by ERA5 reanalysis. Conversely in southern Australia, the wet season occurs in the winter months (JJA). Both QldFCP-2 and NARCliM2.0 show dry biases during this season across simulations, whereas BARPA-ACS and CCAM-ACS possess smaller, balanced biases. Again, the performance of N2.0-R3 is improved compared with N2.0-R5.
All four RCMs indicate similar levels of biases exceeding the benchmark values for summer tasmax (Fig. 3b). In DJF, BARPA-ACS features a consistent warm bias across all ensemble members, whereas both CCAM-ACS and QldFCP-2 show a more varied distribution of bias signs across regions and ensemble members. Winter tasmax are overly cool in BARPA-ACS, NARCLIM2.0 and some CCAM-ACS simulations but are very well represented by QldFCP-2.
The majority of simulations indicate improvement over the tasmin benchmark across both seasons (Fig. 3c). This result is largely due to the high value of the benchmark associated with a persistent warm bias in tasmin across Australia in the CMIP6 ensemble, ranging from 1.62 to 3.25°C. Many NARCliM2.0 ensemble members show a warm bias in DJF in northern Australia, possibly linked to their dry biases. CCAM-ACS-CNRM-ESM2-1 also features strong cold biases in tasmax in both summer and winter. Further investigation (not shown) indicates that in CMIP6, CNRM-ESM2-1 has a substantial (~4°C) cold bias at upper levels over Australia that does not reach the surface. The cold tropospheric temperature bias is the coldest among any GCM (Rahimi et al. 2024). When downscaled with CCAM-ACS, this cold bias extends to the surface, causing the benchmark to not be met.
4.2. Spatial pattern benchmark
The second benchmark assesses the ability of each RCM simulation to reproduce the spatial pattern of the mean state of the three core variables. Following Taylor et al. (2001), a Taylor diagram format has been used to display the assessment. This assessment was performed by first remapping the AGCD observational data to the respective model grid, and secondly computing correlations and standard deviation ratios on each native grid. This benchmark follows Isphording et al. (2024a) in prescribing fixed thresholds for spatial pattern benchmarks. Isphording et al. (2024a) determined these thresholds through consultation with data users on their expectations of model performance. However, in order to implement the Taylor diagram presentation, this approach does diverge from Isphording et al. (2024a) by using cNRMSE instead of MAPE. We note that the cNRMSE benchmark is a stronger condition than the correlation benchmark. Thresholds of 0.7 and 0.65 were used for spatial correlation and cNRMSE, with the former matching Isphording et al. (2024a).
Benchmarks are presented in Fig. 4, which shows Taylor diagrams of the climatological mean core variables, with benchmarks indicated by magenta lines. RCM simulations are indicated by blue, orange, red and green markers with colours indicating the RCM. Where possible, driving GCMs are labelled with an index according to Table 1; however, this label has been omitted where markers overlap.
Taylor diagrams indicating spatial pattern benchmark for core variables: (a) precipitation; (b) tasmax; (c) tasmin. The radial axis indicates the spatial standard deviation of each climatological mean normalised by that of observations. The angle axis indicates the cosine of the spatial correlation between each modelled climatological mean and observations. Curved grey contours show contours of cNRMSE. The black star indicates a hypothetical perfect match between a model and observations. The convex hull of the CMIP6 ensemble is shown by grey shading. Between colours and shapes indicate RCM, numbers indicate GCM. Numbers are only shown when clustering allows. Magenta lines indicate correlation benchmark (dashed) and cNRMSE benchmark (solid). All models pass these benchmarks.

Fig. 4 shows that all models pass the spatial variability benchmarks, with spatial correlations exceeding 0.7 and cNRMSE below 65%. Further analysis (not shown) also indicates that all models had MAPE values below 75% in accordance with the benchmark applied by Isphording et al. (2024a). In all panels, QldFCP-2 shows a very high degree of clustering, owing to the lower impact of inherited GCM biases due to the bias-corrected configuration. Fig. 4a indicates that BARPA-ACS performs well at simulating the standard deviation of precipitation, with most other simulations underestimating metric. All RCM simulations show similar values of correlation between 0.8 and 0.95. By contrast, Fig. 4b indicates that QldFCP-2 and NARCliM2.0 simulate the standard deviation of tasmax very well, whereas BARPA-ACS overestimates and CCAM ACS underestimates the standard deviations. Correlations all exceed 0.95. Finally, minimum temperature spatial patterns (Fig. 4c) are also well simulated by all models, with cNRMSE values less than 40% and correlations above 90%. The simulation of tasmin by NARCliM2.0 is more influenced by the driving GCM than the RCM configuration, because N2.0-R3 and N2.0-R5 simulation pairs with the same driving model tend to cluster together.
4.3. Seasonal cycle benchmark
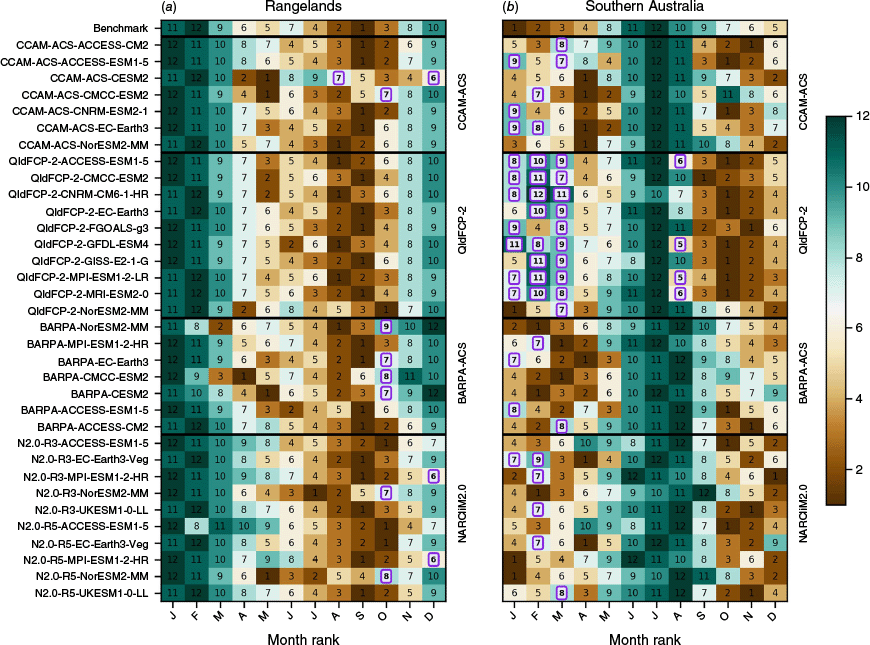
The seasonal cycle benchmark for each NRM region follows the recommendation from Isphording et al. (2024a) for a unimodal seasonal cycle. This requires that the 3-month observed high and low peaks of the seasonal cycle occur within the modelled highest and lowest 6 months of the year respectively. The seasonal cycle benchmark was applied to all three core variables. However, the benchmark was unanimously passed for both temperature variables, and therefore is only presented for precipitation. Figures 5 and 6 indicate the months that meet the seasonal cycle benchmark for precipitation for each super-NRM region, with colours and numbers indicating the ranking of the months from driest (1) to wettest (12). The observed seasonal cycle derived from AGCD is shown in the top row. Following the recommendations of Isphording et al. (2024a), the magnitude of seasonal mean rainfall for each GCM–RCM pair is indicated in Fig. 7. For brevity, this figure does not distinguish between the downscaled GCMs.
Seasonal cycle benchmark following Isphording et al. (2024a) for a unimodal seasonal cycle in (a) northern and (b) eastern Australia. Format follows Fig. 3, where values highlighted in purple indicate where a simulation does not meet our benchmarking standards. Colours and numbers indicate the ranking of monthly mean precipitation, with 1 being the driest and 12 being the wettest.

Annual cycle magnitude and ranges for each RCM for (a) southern Australia, (b) eastern Australia, (c) rangelands and (d) northern Australia. Thick solid lines represent the ensemble mean for each RCM, whereas thinner dotted lines represent the ensemble maximum and ensemble minimum, with colours as per the legend. The observational comparison is shown in black.

Overall, the majority of models pass the seasonal cycle benchmarks for northern Australia, eastern Australia and the rangelands regions, although some RCM simulations, particularly those driven by NorESM2-MM, simulate an early rainfall onset in October in the rangelands region. Southern Australia shows the poorest seasonal cycle results, with all QldFCP-2 showing relatively wet months in late summer during the observed dry season. Analysis of Fig. 7 indicates that this is an artifact of the low winter rainfall in QldFCP-2, rather than excess precipitation during late summer. The driest season in this QldFCP-2 has been shifted to spring and generally produces the largest degree of variability across the GCM–RCM simulation pairs. An inability of models to capture the seasonal cycle over southern Australia is a recurring issue, also seen in CMIP5 (Moise et al. 2015) and the CMIP5 generation of CORDEX-Australasia, particularly in CCAMs (Isphording et al. 2024b). Supplementary material Fig. S3, which shows the benchmark as applied to CMIP6, also indicates that this issue is present in the CMIP6 driving ensemble.
Seasonal cycle analysis is only presented for precipitation, and not tasmax or tasmin. Further analysis (not shown) indicated that all models met the benchmarks in all seasons when the equivalent benchmark definition was applied to tasmax and tasmin. Seasonal progressions of tasmax and tasmin, as per Fig. 7, are provided in Supplementary Fig. S4. Seasonal cycles of temperatures are straightforward sinusoids in most regions, with peaks coinciding with the maximum solar irradiation. The exception to this is tasmax in northern Australia, where the presence of a monsoon shifts the peak to November. Both NARCliM2.0 and BARPA-ACS miss this peak and instead simulate peak temperatures in December.
4.4. Temporal distribution benchmark
The temporal distribution benchmark uses a non-parametric approach to assess the shape of the temporal distribution of super-NRM aggregated daily anomalies. The computation approach is similar to that of the Perkins’ Skill Score (Perkins et al. 2007), although the spatial aggregation masks spatial differences between distributions, causing generally higher values than achieved by a standard Perkins score. This spatial aggregation approach was adapted from Schroeter et al. (2024). Daily core variables are first aggregated over super-NRM regions, and the seasonal mean is then removed. The resulting anomalies are binned into normalised density functions using a 0.2-mm day–1 or 0.2-K bin width. The temporal distribution score is then computed as the sum over all bins of the minimum of the observed or modelled density. As above, the benchmark value is taken as the average temporal distribution score from the CMIP6 ensemble.
Heatmaps of the temporal distribution benchmark are provided in Fig. 8. Despite the removal of the mean, the temporal distribution scores for precipitation are correlated with the bias benchmark presented in Fig. 3, but the temperature-based temporal distribution scores are more independent. The benchmark and RCM values of both temperature temporal distribution scores are all quite high, suggesting that CMIP6 and CORDEX have similar performance at simulating the temporal variability of large-scale temperatures – as may be expected. Tasmax are low in QldFCP-2 in southern Australia for both seasons despite small mean-state biases. Tasmin temporal distribution scores are low in NARCliM2.0 during DJF. Both the benchmark and RCM simulation precipitation temporal distribution scores are low for eastern Australia between July and August, suggesting that the rainfall distribution for this region and season is difficult to simulate.
Temporal distribution score benchmarks for unbiased distributions of (a) daily precipitation; (b) daily maximum temperatures; and (c) minimum temperatures. Presentation is as per Fig. 3. Blue colours indicate better performance, whereas red colours indicate worse performance.

4.5. Long-term trend benchmark
Although the previous benchmarks reviewed in this study consider model performance at simulating a climate assumed to be approximately stationary, the ability to simulate realistic trends is crucial for climate change applications. Isphording et al. (2024a) presented trends in Australian mean rainfall as one of the core minimum standard benchmarks. The appropriate design of a long-term trend benchmark for downscaled climate models is subtle as it must take into account multiple factors. Firstly, interannual and decadal variability are decoupled from reality in the driving GCMs, and so a model should not be penalised for having independent variability. Secondly, there exists a delicate balance between GCM-based and RCM-based trends, and the degree to which a RCM simulation should follow its host model. On one hand, GCMs are often selected for downscaling on the basis of their projected trends (e.g. Grose et al. 2023) and therefore it may be desirable that the RCM simulations follow their host models. On the other hand, if a RCM deviates from its driving model for a legitimate reason, this may be a sign of added value (e.g. Di Virgilio et al. 2020).
For the reasons listed above, we have opted to benchmark against observed trends that have been considered by previous observational studies. To reduce the amount of decadal variability captured in the trends, we have increased the study period for the long-term trend analysis from 30 to 55 years for this benchmark only. In order to account for the influence of the driving GCM trends on the RCM simulation trends, the benchmarks are shown on a scatter-plot where the corresponding GCM trend is shown on the x-axis and the RCM simulation trend on the y-axis (Fig. 9 and 10). The long-term trend benchmark assesses the ability of RCM simulations to capture AGCD-based observed trend signals in the full historical period, from 1960 to 2014. Trends in NRM-aggregated seasonal mean core variables are computed using a Theil–Sen slope estimator (Theil 1950; Sen 1968). Confidence intervals are computed with a significance value of P < 0.05, and the benchmark is deemed to be satisfied if these confidence intervals overlap. Confidence intervals are marked as error bars on the figures for the AGCD-based value and for all simulations for which the RCM-based confidence intervals do not overlap with observations.
Large-scale trend benchmark plots for precipitation: (a) July–August Murray Basin; (b) July–August SSW Flatlands; (c) December–February Monsoonal North (West). The x-axis shows the long-term trend of the GCM and the y-axis shows the long-term trend of the RCM simulation. Total agreement of the GCM and RCM simulation is indicated by the black line. The AGCD-based trend is indicated by the black cross on the black line. Markers are as per Fig. 4. Confidence intervals at the P < 0.05 level are marked for observations and all models that do not meet the benchmark. Models that do not meet the benchmark are indicated in bold.

Large-scale trend benchmark plots for annual mean tasmin (a–d) and tasmax (e–h) as per Fig. 9.

All super-NRM warming trends in AGCD are statistically significant at the P < 0.05 level and are likely to be driven by climate change. As observed rainfall trends are highly seasonal and do not follow NRM supercluster boundaries, rainfall trend benchmarking is only considered for three NRM subclusters and seasons for which observed rainfall trends have previously been studied, namely the Murray Basin (McKay et al. 2023) and SSW-Flatlands (West) during JJA (Raut et al. 2014), and the Monsoonal North West during DJF (Borowiak et al. 2023; Fahrenbach et al. 2024). These NRM subclusters are indicated by solid lines on Fig. 1.
Figures 9 and 10 indicate the large-scale trend plot for the core variables. The figures plot GCM trends on the x-axis against RCM simulation trends on the y-axis. Each RCM simulation ensemble member is indicated by a labelled point, with colour indicating the RCM used and the label indicating the index of the GCM. The black line indicates parity, and the black cross indicates the AGCD-based observed trend.
Fig. 9 indicates that most GCM and RCM simulations studied do not reproduce the magnitude of the observed drying trend in SSW-Flatlands (West) during JJA. This is consistent with the work of Rauniyar et al. (2023), who found a similar result for GCMs only. However, with the exception of QldFCP2-CNRM-CM6-1-HR, all GCM–RCM pairs lie close to the black parity line, suggesting that the large-scale trend is strongly forced by the driving GCM, limiting the capacity of the RCM simulations to ‘correct’ the GCM and produce a drying trend. Confidence intervals of trends from a total of 11 RCM simulations do not overlap with observations. In the Murray Basin, GCM forcing is still strong, although less so than in SSW-Flatlands (West). Confidence intervals are quite wide, reflecting an uncertain change signal, and all RCM simulations pass the benchmark.
In the Monsoonal North West subcluster, there is considerable decoupling between driving GCMs and their downscaled RCM simulations, suggesting that RCMs have more freedom to deviate from their host models in this region. We speculate that this is due to the local internal variability of the Austral monsoon (Sekizawa et al. 2023). The RCM simulation trends are generally reduced compared with the observed trends, and three RCM simulations (BARPA-EC-Earth3, QldFCP-2-MPI-ESM1-2-LR and N2.0-R3-UKESM1-0-LL) have confidence intervals that do not overlap with observations. We note that the wetting trend in the Monsoon North West may be attributable to factors other than increasing greenhouse gases, such as aerosols (Brown et al. 2020).
Fig. 10 indicates that many RCMs have stronger than observed tasmin trends and northern Australian tasmax trends. Tasmax trends in other regions are generally all positive and are well spread around the observed value. QldFCP-2 shows weaker coupling between the driving GCM and downscaled RCM simulations due to the lack of atmospheric driving data in its experimental design. Simulation of temperature trends downscaled using other RCMs in eastern Australia also tend to diverge more from their driving models than in other regions. This could be related to the better simulation of the Great Dividing Range in higher-resolution models. Models with confidence intervals that do not overlap with observations generally show warming trends in excess of the observed trends.
5.ICCLIM index benchmarks
5.1. Benchmark definition
Unlike the majority of the former benchmarks that dealt with spatially aggregated means, the climate index benchmarks have been designed to capture statistics at the RCM’s native grid resolution. This makes a GCM-based benchmark difficult to define, as GCMs are fundamentally unable to represent these statistics. Because of this, the defined benchmark requires that the RCM simulation be able to represent climate indices at the fine scales with at least the same fidelity that the GCMs are able to represent the indices at coarse scales. This is an ambitious and high benchmark, as finer spatial scales are typically harder to reproduce than coarser scales. However, it has been selected so that the benchmarked indices are those with practical application to impact-based studies.
In order to benchmark climate indices across scales, the selected ICCLIM indices (RR1, RX1day, SDII, CWD, CDD, TXx and TNx) were computed from observations both at the GCM length scale (a standard 1.5° grid, onto which the GCMs were also regridded) and at the native RCM resolution. The benchmarks were computed by comparing the GCM-based indices with the former, and applied to the RCM simulation by comparing the RCM simulation based indices to the latter. The benchmark metric was MAPE for precipitation-based indices, and MAE in units of degrees Celsius for temperature-based indices.
5.2. Benchmark performance
The representation of the different rainfall-based climate indices is shown in Fig. 11. Additionally, aggregated biases of these indices are provided in Supplementary Fig. S7. These figures give insight into the way that convection is represented in the respective RCMs, with GCM forcing providing relatively less explanatory power of model performance for CCAM-ACS, BARPA-ACS and QldFCP-2. Wet day frequency is well represented by BARPA-ACS, potentially owing to the convective-memory enhancement to its convection scheme (Howard et al. 2024), whereas CCAM-ACS shows too frequent wet days across most GCMs. The exception here is CCAM-ACS-CESM2, which has improved wet day frequencies but was shown in Fig. 3 to have a strong summer dry bias in northern Australia and rangelands. Conversely, the annual maximum daily rain rate (RX1Day) is very well represented by QldFCP-2, but is overestimated by both BARPA-ACS and CCAM-ACS. However, the representation of rainfall intensity (SDII) is flipped when compared with RX1Day, with many models that perform well at simulating RX1Day performing poorly at SDII. Both wet and dry spell length (CWD and CDD) are well represented, with CDD being particularly well represented by QldFCP-2.
ICCLIM rainfall index benchmarks for (a) RR1, (b) RX1day, (c) SDII, (d) CWD and (e) CDD. Figure structure follows Fig. 3. Lighter colours represent better performance, whereas darker colours indicate worse performance.

The NARCliM2.0 simulations show the greatest degree of inter-RCM spread across all the RCMs. N2.0-R5 shows pronounced underestimations in the number of wet days and overestimations of dry spell lengths when downscaling MPI-ESM1-2-HR and EC-Earth3-Veg, but very good performance at these metrics when downscaling the remaining three GCMs (Fig. 11 and Supplementary Fig. S7). By contrast, N2.0-R3 shows improvements to the simulation of these metrics when downscaling MPI-ESM1-2-HR and EC-Earth3-Veg. This result is consistent with the improvement of the NARCliM2.0 dry bias between N2.0-R3 and N2.0-R5.
Finally, benchmarks for annual maximum daytime and overnight temperatures are given Fig. 12, with aggregated biases presented in Supplementary Fig. S8. Consistent with Fig. 3, BARPA-ACS overestimates maximum temperatures in northern Australia, whereas NorESM2-MM performs poorly when downscaled by QldFCP-2. TNx benchmark performance is closely linked to the DJF biases in tasmin discussed in Section 4.1, with CNRM-ESM2-1 and seven NARCliM2.0 RCMs highlighted in Fig. 12 owing to the former’s cold bias and the latter’s northern Australian warm bias. Most GCMs and RCMs consistently show relatively high TNx errors in southern Australia compared with the other regions.
ICCLIM rainfall index benchmarks for (a) TXx and (b) TNx. Figure structure follows Fig. 3. Lighter colours represent better performance, whereas darker colours indicate worse performance.

6.Discussion
This paper has presented a benchmark-based assessment of 34 Australasian downscaled climate simulations created from a sparse matrix of three RCMs and 15 GCMs. The benchmark methodology was modified from Isphording et al. (2024a) and also followed the ILAMB framework (Collier et al. 2018). The benchmarks assess the performance of each simulation in representing properties of the historical rainfall and screen temperature climatologies. Biases, seasonal cycles and spatial patterns of the mean state are all considered, as well as temporal distributions, long-term trends and a selection of extreme indices. Spatial aggregation follows large-scale climate regions, and a more-detailed breakdown is given in the accompanying ILAMB dashboard.
Table 5 shows the percentage of RCM simulations passing each benchmark across Sections 4 and 5 of this paper. Across all locations, the trend benchmarks referenced to the AGCD data set, seasonal cycle, spatial correlation and cNRMSE exhibit pass rates exceeding 90%. Across all locations, for benchmarks referred to in this study, the pass rate for variables related to minimum temperature (tasmin and TNx) is the highest among all variables except trends and temporal distribution scores in summer in southern Australia. Model performance at simulating rainfall intensity and maximum annual daily rain rates was also low, especially over northern Australia, although we note the role of observational uncertainty is high in these metrics (Section 3). Spatially, the low pass rates are almost equally distributed in four super NRM regions. For aggregation biases and temporal distribution scores, the pass rate of austral winter tasmin and tasmax are relatively lower in southern Australia and rangelands compared with in the other two regions.
| Variables | NA (%) | EA (%) | SA (%) | R (%) | All (%) | ||
|---|---|---|---|---|---|---|---|
| Aggregated bias (DJF) | Pr | 67.7 | 70.6 | 85.3 | 79.4 | 75.7 | |
| tasmax | 41.2 | 50.0 | 38.2 | 58.8 | 47.1 | ||
| tasmin | 73.5 | 97.1 | 100.0 | 94.1 | 91.2 | ||
| Aggregated bias (JJA) | Pr | 61.8 | 64.7 | 50.0 | 73.5 | 62.5 | |
| tasmax | 85.3 | 79.4 | 64.7 | 61.8 | 72.8 | ||
| tasmin | 94.1 | 100.0 | 97.1 | 100.0 | 97.8 | ||
| Temporal distribution scores (DJF) | Pr | 55.9 | 70.6 | 82.4 | 73.5 | 70.6 | |
| tasmax | 52.9 | 76.5 | 61.8 | 70.6 | 65.4 | ||
| tasmin | 67.7 | 76.5 | 29.4 | 67.7 | 60.3 | ||
| Temporal distribution scores (JJA) | Pr | 47.1 | 44.1 | 61.8 | 47.1 | 50.0 | |
| tasmax | 64.7 | 85.3 | 32.4 | 50.0 | 58.1 | ||
| tasmin | 67.6 | 85.3 | 73.5 | 61.8 | 72.1 | ||
| 1960–2014 temperature trends | tasmax | 81.3 | 100.0 | 93.8 | 96.9 | 93.0 | |
| tasmin | 87.5 | 100.0 | 81.3 | 90.6 | 89.8 | ||
| 1960–2014 precipitation trendsA | SSWF-W (JJA) | 61.8A | |||||
| MB (JJA) | 100.0A | ||||||
| MN-W (DJF) | 91.2A | ||||||
| Seasonal cycle | Pr | 100.0 | 97.1 | 29.4 | 70.6 | 74.3 | |
| Spatial correlation | Pr | 100.0 | 100.0 | ||||
| tasmax | 100.0 | 100.0 | |||||
| tasmin | 100.0 | 100.0 | |||||
| cNRMSE | Pr | 100.0 | 100.0 | ||||
| tasmax | 100.0 | 100.0 | |||||
| tasmin | 100.0 | 100.0 | |||||
| MAE | TXx | 47.1 | 67.7 | 94.1 | 88.2 | 74.3 | |
| TNx | 76.5 | 100.0 | 100.0 | 97.1 | 93.4 | ||
| MAPE | RR1 | 50.0 | 85.3 | 58.8 | 82.4 | 69.1 | |
| RX1day | 64.7 | 47.1 | 58.8 | 61.8 | 58.1 | ||
| CWD | 79.4 | 85.3 | 41.2B | 85.3 | 72.8 | ||
| CDD | 73.5 | 85.3 | 88.2 | 91.2 | 84.6 | ||
| SDII | 14.7 | 58.8 | 82.4B | 26.5B | 45.6 | ||
Pink indicates the percentage of ensembles meeting the benchmark is below 50%. Green indicates this percentage exceeds 90%. NRM superclusters are represented by initials NA (northern Australia), EA (eastern Australia), SA (southern Australia) and R (rangelands).
A comparison between Fig. 3 and Supplementary Fig. S1 reveals the role of GCMs in driving the sign and magnitude of mean state rainfall biases in the different RCM simulations. Owing to the use of bias-corrected SSTs and lack of lateral boundary forcing or nudging, GCMs show very little influence on QldFCP-2. NorESM2-MM is the exception to this, and shows a warm, dry bias when downscaled by QldFCP-2. This model also results in large biases when downscaled by the other RCMs, demonstrating large cold and wet biases in JJA. When downscaled by BARPA-ACS and CCAM-ACS, persistent DJF wet biases in eastern and southern Australia and rangelands propagate through to the RCM simulations from ACCESS-CM2, ACCESS-ESM1.5, CESM2 and NorESM2-MM, as does EC-Earth’s country-wide winter dry bias. Similarly, dry biases in MPI-ESM1-2-HR (both seasons) and EC-Earth3-Veg (JJA only) propagate into both NARCliM2.0 models.
Temperature biases show similar patterns in propagating through the RCM simulations, although the impact can be less straightforward. Winter cold biases are inherited by NARCliM2.0, BARPA-ACS and CCAM-ACS when downscaling ACCESS-CM2, UK-ESM1-0-LL and NorESM2-MM. Tasmin is persistently improved across the RCM ensemble; however, most models show warm biases in winter consistent with the sign of the CMIP6 bias. CCAM-ACS-CNRM-ESM2-1 demonstrates a very cold bias in both tasmax and tasmin that is not reflected in Supplementary Fig. S1. However, further analysis indicates that this CNRM-ESM2-1 possesses a very strong cold bias in the upper atmosphere that does not propagate to the surface, possibly owing to compensating errors with the surface scheme. As CCAM-ACS uses a different surface scheme, the cold bias does propagate to the surface in the downscaled model. Overall, a majority (78%) of RCM simulations show improvement over the GCM-based ensemble mean.
Both the CCAM-ACS and the QldFCP-2 projections were created using the CCAM atmospheric model, with contrasting experimental designs. In order to enable comparison of the experimental designs, these modelling centres have collaborated to keep the model configurations as similar as possible. As CCAM uses a global stretched grid, neither configuration uses fixed lateral boundary conditions in the traditional sense. Instead, CCAM-ACS applies spectral nudging to align the large-scale atmospheric circulation closely to the driving GCM, whereas the atmosphere-only QldFCP-2 models considered in this study allow the atmospheric circulation to develop independently of the GCM and make use of only the SST from the driving model. This approach allows QldFCP-2 to apply a straightforward bias correction to the SST, eliminating SST-driven mean-state biases.
The most intuitive and apparent consequence of these differing experimental designs lies in the mean-state biases, where QldFCP-2 is largely immune to the biases of the driving model, but does feature persistent biases such as a dry bias in southern Australia during winter and a cold bias in northern Australia during summer. By contrast, biases in CCAM-ACS are more closely tied to their driving models, as discussed above. QldFCP-2 models also show more independence from their driving models in the direction of trend (Fig. 7–9) compared with CCAM-ACS. This suggests that those trends may be driven by forms of variability other than SST trends. As the QldFCP-2 experiments have been designed to include a greater degree of variability from the driving GCMs, the GCM-consistency benchmark is less relevant to this model.
More subtle differences between QldFCP-2 and CCAM-ACS are present in their representation of precipitation extreme indices (Fig. 10 and Supplementary Fig. S7). QldFCP-2 performs very well at simulating annual maximum daily precipitation but underestimates the precipitation intensity index, whereas CCAM-ACS overestimates maximum daily precipitation but stimulates the intensity index very well. Further investigation of the precipitation distributions in North Queensland (not shown) indicates that QldFCP-2 overestimates low precipitation rates below 10 mm day–1 and underestimates high rain rates, as is typical of convection-parameterised climate models. CCAM-ACS shows a similar overestimation of low precipitation rates, but also overestimates very high precipitation rates in excess of 100 mm day–1. Although this may suggest that CCAM-ACS simulates SDII well for the wrong reasons, we do note that hazard-relevant precipitation rates between 10 and 100 mm day–1 are very well simulated in CCAM-ACS. By contrast, QldFCP-2 accurately represents the tail of the distribution between 200 and 400 mm day–1. Further analysis has indicated that the high rain-rates in CCAM-ACS are associated with cyclones and tropical lows in northern Australia. Further CCAM development and testing is now under way to further understand and resolve this issue. This case study highlights the capability of multimodel benchmarking in identifying model development priorities.
The benchmarking framework applied in this performance assessment process aimed to be systematic and fair. We decided to interpret each benchmark as a reference point of good performance for each metric assessed, rather than a hard binary to exclude models. All models were shown to have their own strengths and weaknesses on different benchmarks, and this paper has aimed to characterise these, rather than recommend a subset of the CMIP6 ensemble for use in impact studies. Indeed, this study has not found any conclusive evidence that any of the 34 downscaled climate projections should be excluded on the basis of model performance.
The benchmarking approach taken in this study does not attempt to quantify the added value that each RCM simulation has on top of its driving GCM (e.g. Di Virgilio et al. 2020). Added value approaches directly compare each RCM with its host model and directly quantify the improvements gained through downscaling. By contrast, this benchmarking approach assesses the performance across the RCM ensemble from a level footing, disregarding any advantage or disadvantage a RCM may have owing to the inherent biases in the driving data. Added value approaches have equal value, and the added value of the CORDEX-CMIP6-Australasia ensemble needs to be assessed in future work. Some studies already address this, e.g. Chapman et al. (2023). However, as different downscaling experimental designs are capable of adding value to GCM projections in different ways, bespoke added value approaches focussing on a single RCM may be more appropriate than broad, systematised comparisons.
As expected, the process of defining fair and systematic benchmarks was found to be difficult at times and limitations remain in the defined benchmarks. For example, the mean performance across the subset of CMIP6 GCMs downscaled by at least one participating RCM was taken as a benchmark for aggregated biases, temporal distributions and ICCLIM indices. Although useful at assessing large-scale performance, this driving model-based approach cannot assess performance at length scales that are not simulated by the GCMs. As a consequence, we have not been able to benchmark the fine-scale features of the RCM simulations. Additionally, the benchmark applied to the ICCLIM indices sets a high bar, by expecting RCM simulation performance at the fine-scale to be on par with GCM performance at the coarse scale. This approach has been selected because the RCM simulations extreme index data will ultimately be used at fine scales. Previous studies in projects such as HighResMip (e.g. Wehner et al. 2021) indicate that altough increasing resolution of atmospheric models can add value by including extreme rainfall information at greater length scales, like-for-like comparison of coarsened extreme climate indices tends to yield similar performance between high-resolution and low-resolution models.
Additionally, the benchmarking of long-term trends in RCMs has proved to be non-straightforward. We elected to benchmark only against significant observed trends that have been attributed to climate change, in contrast to the approach taken by Isphording et al. (2024a). However, we found that the underlying trend of the driving GCM can play a strong role in driving long-term trends in RCM simulations. Therefore, the trend of the driving GCM must be taken into account when examining the long-term downscaled trends.
Future development of climate model benchmarking approaches should focus on improving the objectivity and acceptance of universal benchmarks, which may aim to achieve a more stringent approach in the future. Process-based benchmarks, including assessment of atmospheric circulation (Grose et al. 2017, 2019), emergent constraints (Simpson et al. 2021) and GCM and RCM compatibility have the potential to improve the rigour of benchmarking approaches. Benchmarks may also be tuneable to Earth system phenomena that create climate hazards such as flooding, bushfires, heatwaves and hail. Further investigation into the implications of model performance against the benchmarks considered in this study is also necessary. For example, can a relationship be drawn between benchmark performance and the future climate change signal? How does benchmarking historical model performance affect confidence in climate projections (e.g. Isphording et al. 2024b)? Can a rigorous benchmarking approach be used to rule out particular pathways of warming, and conversely, might an overly prescriptive benchmarking approach falsely dismiss a plausible warming pathway?
The benchmarks presented in this study assess model biases, spatial patterns and extreme properties, which are typically removed from RCM simulation outputs through bias correction ahead of downstream-impact modelling (e.g. Vogel et al. 2023). Therefore, the relationship between benchmarking results and model performance post-bias correction also needs to be considered. Further analysis should consider whether benchmarking performance can be used to distinguish which models will react to bias correction in unexpected ways. New benchmarks may need to be designed to assess the performance of bias-corrected climate data. Additionally, recent advances in machine learning offer hybrid dynamical–statistical approaches that may be useful in ensemble boosting and improved quantification of uncertainties associated with hazard-type diagnostics. Rigorous evaluation and benchmarking techniques will need to be developed for assessment of these ensembles.
7.Conclusions
This paper presents seven benchmarks that assess the ability of the CORDEX-Australasia CMIP6 ensemble to represent the mean state, extremes and long-term trends of Australia’s recent climate. These benchmarks assess aspects of the climate such as biases, spatial and temporal patterns, and seasonality. Design of the benchmarking methodology has drawn on both the framework presented by Isphording et al. (2024a) and ILAMB (Collier et al. 2018). Each of the 39 models assessed show strengths and weaknesses, which give insights into the impact of the downscaling model, driving model and experimental design on performance. Systematic biases have been identified in RCM downscaling models, which should be targeted in future model development and evaluation. However, on the whole, the downscaled climate simulations considered here have been found to be suitable for downstream climate-change impact studies. The results presented here may be used to create RCM simulation subsets for impact study purposes; however, no recommendations have been presented regarding the inclusion or rejection of ensemble members on performance grounds. Future work could apply the same benchmarking framework to evaluate CMIP-based downscaled models, including comparisons between CMIP5 and CMIP6, and extend this approach to assess future versions of CMIP.
Data availability
The RCM simulation data are published through the Australian National Computational Infrastructure. The QldFCP-2 data set created by QFCSP (see https://doi.org/10.25914/h0bx-be42 for 20-km grid spacing and https://doi.org/10.25914/2c0z-8t40 for 10-km grid spacing). CCAM-ACS is available from https://doi.org/10.25914/rd73-4m38. NARCliM2.0 is available from https://doi.org/10.25914/ysxb-rt43. BARPA-ACS is available from https://doi.org/10.25914/z1x6-dq28. CMIP6 data are available through the Earth System Grid Federation at: http://esgf.llnl.gov/. Replicated data are available from NCI as ESGF Tier 1 node (see https://doi.org/10.25914/5b98afc88531e). AGCD data used in this study are the CSIRO’s commercially licensed version of the Bureau’s AGCD data set on NCI (see https://doi.org/10.25914/6009600304b02). The analysis code and supplementary ILAMB dashboard are available from GitHub (see https://github.com/AusClimateService/Benchmarking and https://ausclimateservice.github.io/benchmarking_ilamb_dashboard/). These resources are additionally preserved on Zenodo (Jiang et al. 2024).
Conflicts of interest
Jatin Kala is an Associate Editor of the Journal of Southern Hemisphere Earth Systems Science, but was not involved in the peer review or decision-making process for this paper. The authors declare that they have no further conflicts of interest.
Declaration of funding
This work was supported by the Australian Climate Service (ACS). NARCliM2.0 is supported by the New South Wales Department of Climate Change, Energy, the Environment and Water with funding provided by the NSW Climate Change Fund, the NSW Climate Change Adaptation Strategy Program, and the ACT, SA, WA and Vic. Governments. QldFCP-2 is supported by the Queensland Future Climate Science Program and funded by the Queensland Government. R. N. Isphording is supported by ARC Centre of Excellence for Climate Extremes (CLEX) (ARC grant number CE170100023) and a Scientia PhD scholarship from UNSW (program code 1476).
Acknowledgements
X. Jiang, E. Howard, C.-H. Su, S. Narsey, B. Ng, M. Thatcher and M. Grose acknowledge the support provided by the Australian Climate Service (ACS) for this research, and the production and publication of BARPA-ACS and CCAM-ACS. J. Syktus, S. Chapman and R. Trancoso acknowledge support by Dr Richard Matear from CSIRO Environment and Dr Marlies Hankel from The University of Queensland for providing computational resources on the National Computational Infrastructure (NCI) and Lindsay Brebber from Information and Digital Science Delivery of the Department of Environment and Science for support with high performance computing and data storage. F. Ji, G. Di Virgilio and J. Kala acknowledge support by the NSW Department of Climate Change, Energy, the Environment, and Water as part of the NARCliM2.0 dynamical downscaling project, contributing to CORDEX Australasia. R. N. Isphording acknowledges the Traditional Custodians of the Bedegal and Gadigal land on which she lives and works. We acknowledge the World Climate Research Programme, which, through its Working Group on Coupled Modelling, coordinated and promoted CMIP6. We thank the climate modelling groups for producing and making available their model output, the ESGF for archiving the data and providing access, and the multiple funding agencies who support CMIP6 and ESGF. Analyses and data storage were completed using resources and services provided by NCI, which is supported by the Australian Government. We thank Dörte Jakob, Roger Bodman and two anonymous reviewers for their constructive comments on this manuscript. This collaboration was supported by the Australian National Partnership for Climate Projections.
References
Abramowitz G (2005) Towards a benchmark for land surface models. Geophysical Research Letter 32, L22702.
| Crossref | Google Scholar |
Abramowitz G (2012) Towards a public, standardized, diagnostic benchmarking system for land surface models. Geoscientific Model Development 5, 819-827.
| Crossref | Google Scholar |
Ahn M-S, Gleckler PJ, Lee J, Pendergrass AG, Jakob C (2022) Benchmarking simulated precipitation variability amplitude across timescales. Journal of Climate 35, 6773-6796.
| Crossref | Google Scholar |
Ahn M-S, Ullrich PA, Gleckler PJ, Lee J, Ordonez AC, Pendergrass AG (2023) Evaluating precipitation distributions at regional scales: a benchmarking framework and application to CMIP5 and 6 models. Geoscientific Model Development 16, 3927-3951.
| Crossref | Google Scholar |
Alexander LV, Arblaster JM (2009) Assessing trends in observed and modelled climate extremes over Australia in relation to future projections. International Journal of Climatology 29, 417-435.
| Crossref | Google Scholar |
Alexander LV, Arblaster JM (2017) Historical and projected trends in temperature and precipitation extremes in Australia in observations and CMIP5. Weather and Climate Extremes 15, 34-56.
| Crossref | Google Scholar |
Aoun A, Pagé C, Tatainova N, Pivan X, Bärring L, Bourgault P, Gasteratos P, Irving D, bascrezee (2024) cerfacs-globc/icclim: 7.0.0. Zenodo 2024, v7.0.0.
| Crossref | Google Scholar |
Bador M, Boé J, Terray L, et al. (2020) Impact of higher spatial atmospheric resolution on precipitation extremes over land in global climate models. Journal of Geophysical Research: Atmospheres 125, e2019JD032184.
| Crossref | Google Scholar |
Borowiak A, King A, Lane T (2023) The link between the Madden–Julian Oscillation and rainfall trends in northwest Australia. Geophysical Research Letters 50, e2022GL101799.
| Crossref | Google Scholar |
Brown JR, Colman RA, Narsey S, Moise AF (2020) Sensitivity of Australian monsoon rainfall to aerosol direct and indirect effects under a range of emission scenarios. Bureau Research Report 44. (Australian Bureau of Meteorology: Melbourne, Vic., Australia) Available at https://nla.gov.au/nla.obj-2821916623/view
Chapman S, Syktus J, Trancoso R, Thatcher M, Toombs N, Wong KK-H, Takbash A (2023) Evaluation of dynamically downscaled CMIP6-CCAM models over Australia. Earth’s Future 11, e2023EF003548.
| Crossref | Google Scholar |
Clarke J, Webb L, Hennessy K (2015) Chapter 2. User needs and regionalisation. In ‘Climate Change in Australia: Projections for Australia’s NRM Regions’. (Eds M Ekström, C Gerbing, M Grose, J Bhend, L Webb, J Risbey, CSIRO and Bureau of Meteorology) Technical Report, pp. 13–21. (CSIRO and Bureau of Meteorology, Australia) Available at https://www.climatechangeinaustralia.gov.au/media/ccia/2.2/cms_page_media/168/CCIA_2015_NRM_TechnicalReport_WEB.pdf
Clarke J, Grose M, Thatcher M, Hernaman V, Heady C, Round V, Rafter T, Trenham C, Wilson L (2019) Victorian Climate Projections 2019 Technical Report. (CSIRO) Available at https://www.climatechangeinaustralia.gov.au/en/projects/victorian-climate-projections-2019/
Collier N, Hoffman FM, Lawrence DM, Keppel-Aleks G, Koven CD, Riley WJ, et al. (2018) The International Land Model Benchmarking (ILAMB) system: design, theory, and implementation. Journal of Advances in Modeling Earth Systems 10, 2731-2754.
| Crossref | Google Scholar |
CSIRO, Bureau of Meteorology, and Australian Energy Market Operator (2021) ESCI Project Final report. Available at https://www.climatechangeinaustralia.gov.au/media/ccia/2.2/cms_page_media/799/ESCI%20Project%20final%20report_210721.pdf [Verified 24 September 2024]
Di Virgilio G, Evans JP, Di Luca A, et al. (2020) Realised added value in dynamical downscaling of Australian climate change. Climate Dynamics 54, 4675-4692.
| Crossref | Google Scholar |
Di Virgilio G, Ji F, Tam E, Nishant N, Evans JP, Thomas C, et al. (2022) Selecting CMIP6 GCMs for CORDEX dynamical downscaling: model performance, independence, and climate change signals. Earth’s Future 10, e2021EF002625.
| Crossref | Google Scholar |
Di Virgilio G, Ji F, Tam E, Evans JP, Kala J, Andrys J, Thomas C, Choudhury D, Rocha C, Li Y, Riley ML (2025a) Evaluation of CORDEX ERA5-forced NARCliM2.0 regional climate models over Australia using the Weather Research and Forecasting (WRF) model version 4.1.2. Geoscientific Model Development 18, 703-724.
| Crossref | Google Scholar |
Di Virgilio G, Evans JP, Ji F, Tam E, Kala J, Andrys J, Thomas C, Choudhury D, Rocha C, White S, Li Y, El Rafei M, Goyal R, Riley ML, Lingala J (2025b) Design, evaluation, and future projections of the NARCliM2.0 CORDEX-CMIP6 Australasia regional climate ensemble. Geoscientific Model Development 18, 671-702.
| Crossref | Google Scholar |
Evans JP, Ji F, Lee C, Smith P, Argüeso D, Fita L (2014) Design of a regional climate modelling projection ensemble experiment – NARCliM. Geoscientific Model Development 7, 621-629.
| Crossref | Google Scholar |
Evans JP, Di Virgilio G, Hirsch AL, et al. (2021) The CORDEX-Australasia ensemble: evaluation and future projections. Climate Dynamics 57, 1385-1401.
| Crossref | Google Scholar |
Eyring V, Bony S, Meehl GA, Senior CA, Stevens B, Stouffer RJ, Taylor KE (2016) Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geoscientific Model Development 9, 1937-1958.
| Crossref | Google Scholar |
Eyring V, Bock L, Lauer A, Righi M, Schlund M, Andela B, Arnone E, Bellprat O, Brötz B, Caron L-P, Carvalhais N, Cionni I, Cortesi N, Crezee B, Davin EL, Davini P, Debeire K, de Mora L, Deser C, Docquier D, Earnshaw P, Ehbrecht C, Gier BK, Gonzalez-Reviriego N, Goodman P, Hagemann S, Hardiman S, Hassler B, Hunter A, Kadow C, Kindermann S, Koirala S, Koldunov N, Lejeune Q, Lembo V, Lovato T, Lucarini V, Massonnet F, Müller B, Pandde A, Pérez-Zanón N, Phillips A, Predoi V, Russell J, Sellar A, Serva F, Stacke T, Swaminathan R, Torralba V, Vegas-Regidor J, von Hardenberg J, Weigel K, Zimmermann K (2020) Earth System Model Evaluation Tool (ESMValTool) v2.0 – an extended set of large-scale diagnostics for quasi-operational and comprehensive evaluation of Earth system models in CMIP. Geoscientific Model Development 13, 3383-3438.
| Crossref | Google Scholar |
Fahrenbach NLS, Bollasina MA, Samset BH, Cowan T, Ekman AML (2024) Asian anthropogenic aerosol forcing played a key role in the multidecadal increase in Australian summer monsoon rainfall. Journal of Climate 37, 895-911.
| Crossref | Google Scholar |
Fiedler S, Crueger T, D’Agostino R, et al. (2020) Simulated tropical precipitation assessed across three major phases of the Coupled Model Intercomparison Project (CMIP). Monthly Weather Review 148, 3653-3680.
| Crossref | Google Scholar |
Flato G, Marotzke J, Abiodun B, et al. (2013) Evaluation of climate models. In ‘Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change’. (Eds TF Stocker et al.) pp. 753–759. (Cambridge University Press) Available at https://www.ipcc.ch/site/assets/uploads/2018/02/WG1AR5_Chapter09_FINAL.pdf
Gates WL (1992) AMIP: the Atmospheric Model Intercomparison Project. Bulletin of the American Meteorological Society 73, 1962-1970.
| Crossref | Google Scholar |
Giorgi F (2019) Thirty years of regional climate modeling: where are we and where are we going next? Journal of Geophysical Research: Atmospheres 124, 2018JD030094.
| Crossref | Google Scholar |
Giorgi F, Coppola E, Jacob D, Teichmann C, Omar SA, Ashfaq M, Ban N, Bülow K, Bukovsky M, Buntemeyer L, Cavazos T, Ciarlo‘ J, da Rocha RP, Das S, di Sante F, Evans JP, Gao X, Giuliani G, Glazer RH, Hoffmann P, Im E-S, Langendijk G, Lierhammer L, Llopart M, Mueller S, Luna-Nino R, Nogherotto R, Pichelli E, Raffaele F, Reboita M, Rechid D, Remedio A, Remke T, Sawadogo W, Sieck K, Torres-Alavez JA, Weber T (2021) The CORDEX-CORE EXP-I Initiative: description and highlight results from the initial analysis. Bulletin of the American Meteorological Society 103, E293-E310.
| Crossref | Google Scholar |
Grose MR, Risbey JS, Moise AF, Osbrough S, Heady C, Wilson L, Erwin T (2017) Constraints on southern Australian rainfall change based on atmospheric circulation in CMIP5 simulations. Journal of Climate 30, 225-242.
| Crossref | Google Scholar |
Grose MR, Foster S, Risbey JS, Osbrough S, Wilson L (2019) Using indices of atmospheric circulation to refine southern Australian winter rainfall climate projections. Climate Dynamics 53, 5481-5493.
| Crossref | Google Scholar |
Grose MR, Narsey S, Trancoso R, Mackallah C, Delage F, Dowdy A, Di Virgilio G, Watterson I, Dobrohotoff P, Rashid HA, Rauniyar S, Henley B, Thatcher M, Syktus S, Abramowitz G, Evans JP, Su C, Takbash A (2023) A CMIP6-based multi-model downscaling ensemble to underpin climate change services in Australia. Climate Services 20, 100368.
| Crossref | Google Scholar |
Gutiérrez JM, Jones RG, Narisma GT, Alves LM, Amjad M, Gorodetskaya IV, Grose M, Klutse NAB, Krakovska S, Li J, Martínez-Castro D, Mearns LO, Mernild SH, Ngo-Duc T, van den Hurk B, Yoon J-H (2021) Atlas. In ‘Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change’. (Eds V Masson-Delmotte, P Zhai, A Pirani, SL Connors, C Péan, S Berger, N Caud, Y Chen, L Goldfarb, MI Gomis, M Huang, K Leitzell, E Lonnoy, JBR Matthews, TK Maycock, T Waterfield, O Yelekçi, R Yu, B Zhou) pp. 1927–2058. (Cambridge University Press: Cambridge, UK; and New York, NY, USA) 10.1017/9781009157896.021
Gutowski WJ, Jr, Giorgi F, Timbal B, Frigon A, Jacob D, Kang HS, Raghavan K, Lee B, Lennard C, Nikulin G, O’Rourke E, Rixen M, Solman S, Stephenson T, Tangang F (2016) WCRP Coordinated Regional Downscaling Experiment (CORDEX): a diagnostic MIP for CMIP6. Geoscientific Model Development 9, 4087-4095.
| Crossref | Google Scholar |
Haarsma RJ, Roberts MJ, Vidale PL, Senior CA, Bellucci A, Bao Q, Chang P, Corti S, Fučkar NS, Guemas V, von Hardenberg J, Hazeleger W, Kodama C, Koenigk T, Leung LR, Lu J, Luo JJ, Mao J, Mizielinski MS, Mizuta R, Nobre P, Satoh M, Scoccimarro E, Semmler T, Small J, von Storch JS (2016) High Resolution Model Intercomparison Project (HighResMIP v1.0) for CMIP6. Geoscientific Model Development 9, 4185-4208.
| Crossref | Google Scholar |
Harris IC, Jones PD (2019) CRU TS4.02: Climatic Research Unit (CRU) Time-Series (TS) version 4.02 of high-resolution gridded data of month-by-month variation in climate (Jan. 1901–Dec. 2017). 1 April 2019. (University of East Anglia, Centre for Environmental Data Analysis, Climatic Research Unit) 10.5285/b2f81914257c4188b181a4d8b0a46bff
Hoffmann P, Katzfey JJ, McGregor JL, Thatcher M (2016) Bias and variance correction of sea surface temperatures used for dynamical downscaling. Journal of Geophysical Research 121, 12877-12890.
| Crossref | Google Scholar |
Howard E, Su C-H, Stassen C, Naha R, Ye H, Pepler A, Bell SS, Dowdy AJ, Tucker SO, Franklin C (2024) Performance and process-based evaluation of the BARPA-R Australasian regional climate model version 1. Geoscientific Model Development 17, 731-757.
| Crossref | Google Scholar |
Huffman G, Bolvin D, Braithwaite D, Hsu K, Joyce R, Xie P (2018) Global Precipitation Measurements (GPM) Integrated multi-satellite retrievals (IMERG) L3 half hourly 0.1 degree×0.1 degree v5., Technical report. (NASA) Available at https://docserver.gesdisc.eosdis.nasa.gov/public/project/GPM/IMERG_ATBD_V5.pdf [Verified 19 May 2025]
Isphording RN, Alexander LV, Bador M, Green D, Evans JP, Wales S (2024a) A standardized benchmarking framework to assess downscaled precipitation simulations. Journal of Climate 37, 1089-1110.
| Crossref | Google Scholar |
Isphording RN, Alexander LV, Bador M (2024b) Benchmarking historical model performance increases confidence in regional precipitation projections. ESS Open Archive [Preprint, published 28 September 2024].
| Crossref | Google Scholar |
Ji F, Ekström M, Evans JP, Teng J (2014) Evaluating rainfall patterns using physics scheme ensembles from a regional atmospheric model. Theoretical and Applied Climatology 115, 297-304.
| Crossref | Google Scholar |
Ji F, Di Virgilio G, Nishant N, Tam E, Evans JP, Kala J, Andrys J, Thomas C, Riley M (2024) Evaluation of precipitation extremes in ERA5-driven regional climate simulations over the CORDEX-Australasia domain. Weather and Climate Extremes 44, 100676.
| Crossref | Google Scholar |
Jiang X, Howard E, Isphording R, Ng B (2024) Towards benchmarking the dynamically downscaled CMIP6 CORDEX-Australasia ensemble over Australia: code and dashboard. Zenodo 2024, v1.
| Crossref | Google Scholar |
Jones DA, Wang W, Fawcett R (2009) High-quality spatial climate data-sets for Australia. Australian Meteorological and Oceanographic Journal 58, 233-248.
| Crossref | Google Scholar |
Liu YL, Alexander LV, Evans JP, Thatcher M (2024) Sensitivity of Australian rainfall to driving SST data sets in a variable-resolution global atmospheric model. Journal of Geophysical Research: Atmospheres 129, e2024JD040954.
| Crossref | Google Scholar |
Martinez-Villalobos C, Neelin JD, Pendergrass AG (2022) Metrics for evaluating CMIP6 representation of daily precipitation probability distributions. Journal of Climate 35, 5719-5743.
| Crossref | Google Scholar |
McKay RC, Boschat G, Rudeva I, Pepler A, Purich A, Dowdy A, Hope P, Gillett ZE, Rauniyar S (2023) Can southern Australian rainfall decline be explained? A review of possible drivers. WIREs Climate Change 14, e820.
| Crossref | Google Scholar |
Meyer JDD, Wang S-YS, Gillies RR, Yoon J-H (2021) Evaluating NA-CORDEX historical performance and future change of western US precipitation patterns and modes of variability. International Journal of Climatology 41, 4509-4532.
| Crossref | Google Scholar |
Moise A, Wilson L, Grose M, Whetton P, Watterson I, Bhend J, Bathols J, Hanson L, Erwin T, Bedin T, Heady C, Rafter T (2015) Evaluation of CMIP3 and CMIP5 models over the Australian region to inform confidence in projections. Australian Meteorological and Oceanographic Journal 65, 19-53.
| Crossref | Google Scholar |
Munday C, Washington R (2018) Systematic climate model rainfall biases over southern Africa: links to moisture circulation and topography. Journal of Climate 31, 7533-7548.
| Crossref | Google Scholar |
Nicholls N, Drosdowsky W, Lavery B (1997) Australian rainfall variability and change. Weather 52, 66-72.
| Crossref | Google Scholar |
Nishant N, Evans JP, Di Virgilio G, Downes SM, Ji F, Cheung KKW, Tam E, Miller J, Beyer K, Riley ML (2021) Introducing NARCliM1.5: evaluating the performance of regional climate projections for southeast Australia for 1950–2100. Earth’s Future 9, e2020EF00183.
| Crossref | Google Scholar |
Nishant N, Sherwood S, Prasad A, Ji F, Singh A (2022) Impact of higher spatial resolution on precipitation properties over Australia. Geophysical Research Letters 49, e2022GL100717.
| Crossref | Google Scholar |
Nguyen PL, Alexander LV, Thatcher MJ, Truong SCH, Isphording RN, McGregor JL (2024) Selecting CMIP6 global climate models (GCMs) for Coordinated Regional Climate Downscaling Experiment (CORDEX) dynamical downscaling over southeast Asia using a standardised benchmarking framework. Geoscientific Model Development 17, 7285-7315.
| Crossref | Google Scholar |
Pagé C, Aoun A, Spinuso A (2022) icclim: calculating climate indices and indicators made easy. ESS Open Archive [Preprint, published 28 January 2022].
| Crossref | Google Scholar |
Perkins SE, Pitman AJ, Holbrook NJ, McAneney J (2007) Evaluation of the AR4 climate models’ simulated daily maximum temperature, minimum temperature, and precipitation over Australia using probability density functions. Journal of Climate 20, 4356-4376.
| Crossref | Google Scholar |
Pinto I, Jack C, Hewitson B (2018) Process-based model evaluation and projections over southern Africa from Coordinated Regional Climate Downscaling Experiment and Coupled Model Intercomparison Project Phase 5 models. International Journal of Climatology 38, 4251-4261.
| Crossref | Google Scholar |
Rahimi S, Huang L, Norris J, Hall A, Goldenson N, Risser M, et al. (2024) Understanding the cascade: removing GCM biases improves dynamically downscaled climate projections. Geophysical Research Letters 51, e2023GL106264.
| Crossref | Google Scholar |
Rauniyar SP, Hope P, Power SB, Grose M, Jones D (2023) The role of internal variability and external forcing on southwestern Australian rainfall: prospects for very wet or dry years. Scientific Reports 13, 21578.
| Crossref | Google Scholar | PubMed |
Raut BA, Jakob C, Reeder MJ (2014) Rainfall changes over southwestern Australia and their relationship to the Southern Annular Mode and ENSO. Journal of Climate 27, 5801-5814.
| Crossref | Google Scholar |
Royal Netherlands Meteorological Institute (2021) European Climate Assessment and Dataset. (KNMI) Available at https://knmi-ecad-assets-prd.s3.amazonaws.com/documents/atbd.pdf [Verified 26 September 2024]
Schroeter BJE, Ng B, Takbash A, Rafter T, Thatcher M (2024) A comprehensive evaluation of mean and extreme climate for the Conformal Cubic Atmospheric Model (CCAM). Journal of Applied Meteorology and Climatology 63, 997-1018.
| Crossref | Google Scholar |
Sekizawa S, Nakamura H, Kosaka Y (2023) Interannual variability of the Australian summer monsoon sustained through internal processes: wind–evaporation feedback, dynamical air–sea interaction, and soil moisture memory. Journal of Climate 36, 983-1000.
| Crossref | Google Scholar |
Sen PK (1968)) Estimates of the regression coefficient based on Kendall’s tau. Journal of the American Statistical Association 63, 1379-1389.
| Crossref | Google Scholar |
Sillmann J, Kharin VV, Zhang X, Zwiers FW, Bronaugh D (2013) Climate extremes indices in the CMIP5 multimodel ensemble: Part 1. Model evaluation in the present climate. Journal of Geophysical Research: Atmospheres 118, 1716-1733.
| Crossref | Google Scholar |
Simpson IR, McKinnon KA, Davenport FV, Tingley M, Lehner F, Fahad A, Chen DI (2021) Emergent constraints on the large-scale atmospheric circulation and regional hydroclimate: do they still work in CMIP6 and how much can they actually constrain the future? Journal of Climate 34, 6355-6377.
| Crossref | Google Scholar |
Skamarock WC, Klemp JB, Dudhia J, Gill DO, Liu Z, Berner J, Wang W, Powers JG, Duda MG, Barker DM, Huang XY (2019) A description of the Advanced Research WRF version 4. NCAR Technical Note NCAR/TN-556+STR, National Center for Atmospheric Research, Boulder, CO, USA. 10.5065/1dfh-6p97
Su C-H, Stassen C, Howard E, Ye H, Bell SS, Pepler A, Dowdy AJ, Tucker SO, Franklin C (2022) BARPA: new development of ACCESS-based regional climate modelling for Australian Climate Service. Bureau Research Report 069. (Australian Bureau of Meteorology) Available at http://www.bom.gov.au/research/publications/researchreports/BRR-069.pdf
Taylor KE (2001) Summarizing multiple aspects of model performance in a single diagram. Journal of Geophysical Research 106, 7183-7192.
| Crossref | Google Scholar |
Thatcher M, McGregor JL (2009) Using a scale-selective filter for dynamical downscaling with the Conformal Cubic Atmospheric Model. Monthly Weather Review 137, 1742-1752.
| Crossref | Google Scholar |
Thatcher M, McGregor J, Dix M, Katzfey J (2015) A new approach for coupled regional climate modeling using more than 10,000 cores. IFIP Advances in Information and Communication Technology 448, 599-607.
| Crossref | Google Scholar |
Theil H (1950) A Rank-invariant method of linear and polynomial regression analysis I, II and III. Nederlandse Akademie van Wetenschappen Proceedings 53, 386-392, 521–525, 1397–1412.
| Google Scholar |
Tucker SO, Kendon EJ, Bellouin N, Buonomo E, Johnson B, Murphy JM (2022) Evaluation of a new 12-km regional perturbed parameter ensemble over Europe. Climate Dynamics 58, 879-903.
| Crossref | Google Scholar |
United States Department of Energy (2020) Benchmarking simulated precipitation in Earth system models. Workshop Report DOE/SC-0203. (US DOE, Office of Science, Biological and Environmental Research Program: Germantown, MD, USA) Available at science.osti.gov/-/media/ber/pdf/community-resources/2020/RGMA_Precip_Metrics_workshop.pdf [Verified 7 April 2025]
Vautard R, Kadygrov N, Iles C, Boberg F, Buonomo E, Bülow K, et al. (2021) Evaluation of the large EURO-CORDEX regional climate model ensemble. Journal of Geophysical Research: Atmospheres 126, e2019JD032344.
| Crossref | Google Scholar |
Vogel E, Johnson F, Marshall L, Bende-Michl U, Wilson L, Peter JR, Wasko C, Srikanthan S, Sharples W, Dowdy A, Hope P, Khan Z, Mehrotra R, Sharma A, Matic V, Oke A, Turner M, Thomas S, Donnelly C, Duong VC (2023) An evaluation framework for downscaling and bias correction in climate change impact studies. Journal of Hydrology 622, 129693.
| Crossref | Google Scholar |
Walters D, Baran AJ, Boutle I, Brooks M, Earnshaw P, Edwards J, Furtado K, Hill P, Lock A, Manners J, Morcrette C, Mulcahy J, Sanchez C, Smith C, Stratton R, Tennant W, Tomassini L, Van Weverberg K, Vosper S, Willett M, Browse J, Bushell A, Carslaw K, Dalvi M, Essery R, Gedney N, Hardiman S, Johnson B, Johnson C, Jones A, Jones C, Mann G, Milton S, Rumbold H, Sellar A, Ujiie M, Whitall M, Williams K, Zerroukat M (2019) The Met Office Unified Model Global Atmosphere 7.0/7.1 and JULES Global Land 7.0 configurations. Geoscientific Model Development 12, 1909-1963.
| Crossref | Google Scholar |
Wehner M, Lee J, Risser M, Ullrich P, Gleckler P, Collins WD (2021) Evaluation of extreme sub-daily precipitation in high-resolution global climate model simulations. Philosophical Transactions of the Royal Society – A. Mathematical, Physical and Engineering Sciences 379, 20190545.
| Crossref | Google Scholar |
Wilson L, Bende-Michl U, Sharples W, Vogel E, Peter J, Srikanthan S, Khan Z, Matic V, Oke A, Turner M, Duong VC, Loh S, Baron-Hay S, Roussis J, Kociuba G, Hope P, Dowdy A, Donnelly C, Argent R, Thomas S, Kitsios A, Bellhouse J (2022) A national hydrological projections service for Australia. Climate Services 18, 100331.
| Crossref | Google Scholar |