Brief history and future of animal simulation models for science and application
J. L. BlackJohn L Black Consulting, Warrimoo, NSW 2774, Australia. Email: jblack@pnc.com.au
Animal Production Science 54(12) 1883-1895 https://doi.org/10.1071/AN14650
Submitted: 21 June 2014 Accepted: 16 July 2014 Published: 1 September 2014
Journal Compilation © CSIRO Publishing 2014 Open Access CC BY-NC-ND
Abstract
Mathematical equations have been used to add quantitative rigour to the description of animal systems for the last 100 years. Initially, simple equations were used to describe the growth of animals or their parts and to predict nutrient requirements for different livestock species. The advent of computers led to development of complex multi-equation, dynamic models of animal metabolism and of the interaction between animals and their environment. An understanding was developed about how animal systems could be integrated in models to obtain the most realistic prediction of observations and allow accurate predictions of as yet unobserved events. Animal models have been used to illustrate how well animal systems are understood and to identify areas requiring further research. Many animal models have been developed with the aim of evaluating alternative management strategies within animal enterprises. Several important gaps in current animal models requiring further development are identified: including a more mechanistic representation of the control of feed intake; inclusion of methyl-donor requirements and simulation of the methionine cycle; plus a more mechanistic representation of disease and the impact of microbial loads under production environments. Reasons are identified why few animal models have been used for day-to-day decision making on farm. In the future, animal simulation models are envisaged to function as real-time control of systems within animal enterprises to optimise animal productivity, carcass quality, health, welfare and to maximise profit. Further development will be required for the integration of models that run real time in enterprise management systems adopting precision livestock farming technologies.
Additional keywords: adoption, decision making, farming systems, feed intake, immune response, metabolism, methyl-donor metabolism, monogastrics, ruminants, simulation modelling.
Introduction
The use of mathematical equations to describe components of animal systems has a long history extending over 100 years (Dumas et al. 2008). In 1914, Wood and Yule reflected on predicting the amount of fat, work or milk that could be produced from an animal supplied with a diet containing a known mount of starch equivalents (Wood and Yule 1914). The purpose for developing equations to describe such processes is to add quantitative rigour to the assessment of the likely outcomes from an event based on evaluation of existing knowledge. The process, frequently called ‘simulation modelling’, can involve one equation or the integration of many equations.
The first equations used to predict components of animal systems from the 1920s to the 1960s were ‘static’ models that represented the state of the system for only one instance in time (Brody and Ragsdale 1921; Huxley 1924; Blaxter 1962). These first models were used to describe the growth of animals or animal parts (Huxley and Teissier 1936) and to predict the energy and nutrient requirements for many domestic livestock species at specific liveweights (FAO/WHO 1957, 1965; ARC 1965). However, with the advent and increasing use of computers during the late 1960s and 1970s, the number of equations included in models grew substantially. The models became ‘dynamic’, where time was described explicitly and outcomes were predicted over varying periods of time using varying iteration intervals (Whittemore and Fawcett 1974; Graham et al. 1976). Many of the earlier animal simulation models were based largely on regression equations that described associations between two or more variables and which implied little about the underlying mechanisms controlling operation of the system. Predictions from these models were frequently poor when applied to situations outside the range from which the original data were collected (Black 1995).
The realisation that regression equations were unsuitable for most models, stimulated development of ‘mechanistic’ models based on either the laws of physics and chemistry or on equations with known characteristics derived specifically to represent the perceived mechanisms of a system (Black 1995). The latter equations are known as ‘conceptual’ or ‘deductive’ equations and examples are given by Baldwin and Black (1979) and Thornley (2008) to predict sigmoidal growth curves for animal organs or whole animals. Mechanistic models have been used to describe a range of animal systems, including: nutrient metabolism and energy transactions in individual organs or whole animals using biochemical pathways based on Michaelis–Menten kinetics (Garfinkel 1966; Baldwin and Smith 1971); assessing the effects of skin blood flow rate, wool follicle numbers, absorption of sulfur containing amino acids and pregnancy on the rate of wool growth, wool protein composition, wool follicle cell turnover rate and uptake of sulfur-containing amino acids by other tissues (Black and Reis 1979); wool follicle initiation and development based on the reaction–diffusion theory (Nagorcka and Mooney 1989); and the impact of the climate on animals through the physics of heat exchange between the animal and its environment (Bruce and Clark 1979).
The most important characteristic of effective mechanistic models is that they can predict the outcome of an event before it has been observed. This principle is well demonstrated by the reaction diffusion model of Nagorcka and Mooney (1989) for wool follicle initiation (Black 1995). The model predicted that the number of wool follicles initiated at a specific phase of fetal development would be a function of skin surface area. Adelson (1991) tested the hypothesis by placing either a 2 cm teflon hemisphere or a 2 cm flat disc on opposite sides of a 71 day old fetus after the primary follicles had been initiated but before the secondary follicles were formed. The hemisphere : disc surface area was 2 : 1 and the model predicted that the ratio of secondary : primary follicles would be twice as great for the skin over the hemisphere than over the disc. The experiment showed the secondary : primary follicle ratio to be 2.76 for the hemisphere and 1.33 for the disc, confirming the prediction.
There has been continuing development of animal models over the last 30 years (Dumas et al. 2008), with most being a combination of physical-chemical theory representations and conceptual equations. Nevertheless, a question remains about the value of animal models to science and to practical agriculture. This paper considers reasons for developing animal simulation models, highlights several areas where further development of concepts would be valuable for their application and suggests ways that could improve their use in practical agriculture.
Reasons for developing animal models
The philosophy behind development of computer models to simulate animal systems has been described previously by many authors including Baldwin and Koong (1980) and France and Dijkstra (2000). The two primary reasons for developing mathematical models are (1) to demonstrate, quantitatively, how well a system is understood and then direct future research towards improving that understanding; and (2) to integrate disparate pieces of current knowledge to assist decision making either for prioritising research activities or for direct application by enterprise managers. The former represents a formalisation of the process used by all research scientists whereby ideas and concepts about the operation and control of a system are developed using data obtained from experiments. This procedure leads to the development of hypotheses, the conduct of new experiments and acquisition of more knowledge that allows a deeper understanding of the system. Modelling simply adds rigour by forcing each step in the process to be described quantitatively in terms of mathematical equations and not subjectively. Hypotheses about the operation of a system can be more readily evaluated using mathematical models than with traditional subjective approaches. Inputs or components of the modelled system representing concepts of the mechanisms can be readily changed to test hypotheses and examine the closeness of predictions to experimental observations. Thus, hypotheses can be more thoroughly refined before costly experiments are conducted to improve understanding of the system.
The other major advantage of modelling is that many small systems can be integrated into larger systems. Frequently, the complexity of the interactions in these larger systems is so great that it is impossible for the human mind to follow the consequences of changes to the system over time. For example, the effects of a period of cold weather and differences in stocking density on the growth rate and final body composition of pigs can be predicted by simulation models, but cannot be reasonably deduced because of the interaction between the many factors over time (Black et al. 1993).
In the 1970s and 1980s, the capacity to integrate numerous systems into one model led to the concept that fundamental biological knowledge, when incorporated into simulation models, could be used to assist decision making on farms. Models could integrate numerous parts of an animal system and, combined with a representation of an enterprise structure, they could predict outcomes of productivity over long periods of time. These predictions could be used to help managers make decisions about the most profitable strategies to adopt. Numerous models with this intention were developed, including those for pigs (Whittemore 1983; Black et al. 1986; Moughan et al. 1987; de Lange et al. 2001; van Milgen et al. 2008), for sheep (Graham et al. 1976), for beef and dairy cattle (Oltjen et al. 1986; Baldwin et al. 1987a, 1987b, 1987c; Nagorcka and Zurcher 2002) and for poultry (Emmans 1981; Emmans and Fisher 1986; Emmans 1989; Johnston and Gous 2006).
Most models designed for practical application have a similar structure (Oltjen et al. 1986; Emmans and Oldham 1988; Baldwin 1995; Black and de Lange 1995; Ferguson 2006; van Milgen et al. 2008). The animal component of the models commences with a description of the animal, including: an estimate of its genetic potential to deposit protein and energy (or fat); a description of the diet; of the social and climatic environment; and of health status. Feed intake is predicted either from simple algorithms or a complex set of equations (Poppi 2008; Black 2009). Ingested feed is then digested, again using either simple algorithms (Graham et al. 1976) or complex models of digestion, particularly for ruminants (Black et al. 1981; Dijkstra et al. 1992; Baldwin 1995; Nagorcka et al. 2000) and also for pigs (Bastianelli and Sauvant 1998; Rivest et al. 2000). Individual nutrients available for metabolism are predicted. Most models estimate the energy and individual amino acids needed for maintaining the integrity of the animal in relation to its current physiological state and the impact of the social, climatic and disease environment. Several models simulate the requirements for macrominerals (Kebreab et al. 2008). Various procedures, including Michaelis–Menten kinetics and simpler algorithms, are then used to partition available nutrients between competing body functions. The net outcomes from considering these metabolic processes are predictions of accumulation rates of protein, fat, specific minerals, total animal weight, carcass weight, wool growth rates, milk yield, excretion of nitrogen, methane and minerals, efficiency of feed use and other variables. Some models predict the order of limiting amino acids and the amount required to overcome any deficiency. Similarly, deficiencies in macromineral supply and effects on bone strength are also predicted by some models (Black 2009). The majority of current animal models are deterministic and predict the outcome for one animal that represents the mean of a group of similar animals, rather than being stochastic where a range of possible outcomes representing natural variability is predicted. Nevertheless, stochastic elements have been added to several deterministic models by (1) undertaking multiple simulations within one ‘run’ of the model where input variables under either genetic control, such as capacity to deposit fat and protein, or environmental control are varied for each simulation to accommodate all animals within a group (Knap 1995; Baudracco et al. 2013), and (2) using normal curve and statistical variance assumptions for economically important variables such as carcass weight and back fat thickness in pigs to predict their likely frequency and range for determining prices paid for all animals in a group (Black et al. 1993). Stochastic modelling of individual animals has been used in broiler models as a means for determining optimum economic amino acid concentrations in diets (Gous and Berhe 2006), for assessing animal movement within areas (Preisler et al. 2004; Smouse et al. 2010) and for predicting the spread of diseases through animal populations (Rorres et al. 2011; Stevenson et al. 2013). Models have been used to predict the spread of contagious diseases such as spongiform encephalopathy (Thornley and France 2008) and foot-and-mouth disease (Thornley and France 2009).
Most models cited above could generally be described as ‘robust’ and predict animal performance under a range of circumstances with reasonable accuracy. Components of several models continue to be upgraded and improved. New components are being added including representations of disease (Sandberg et al. 2006; Black 2009), macromineral balances and greenhouse gas emissions (Rigolot et al. 2010). Several models include components that allow the exploration of strategies to ameliorate environmental pollution from cattle including methane emissions (Ellis et al. 2008), nitrogen (Ellis et al. 2011) and phosphorus (Kebreab et al. 2008).
Some models predict enterprise profitability and cash flow, while others identify management strategies that optimise the use of enterprise resources for maximum profit (Black et al. 1993; Gous and Berhe 2006). Others contain ‘expert systems’ to aid the interpretation of model outputs by people other than those involved in construction of the model (Menzies et al. 1990; Oltjen et al. 1990). Several animal models are also linked directly to least-cost diet formulation software where nutrient requirements predicted by the simulation model are transferred to a diet formulation predictor (Black et al. 1993; de Lange et al. 2001; Ferguson 2014; Gous 2014).
Although many models have been of substantial value for analysing specific farm enterprise options (de Lange et al. 2001; Nagorcka and Zurcher 2002; Black and Banhazi 2013; Ferguson 2014; Gous 2014), their uptake by industry has been less than anticipated. The models have been valuable for assessing the impacts of alternative management strategies in isolated applications and for setting research priorities, but they have not been used for day-to-day decision making as had been envisaged by many of the model developers. The remainder of this paper examines several areas where models could be improved to better predict reality of animal performance and what may be needed to encourage their use for everyday decision making on farm.
Gaps in animal nutrition models
Several important areas of animal models must be improved to more effectively simulate the performance of commercially raised livestock. The following three are considered: prediction of feed intake and incorporation of maximum energy intake into diet formulation software; inclusion of methyl-donor metabolism and requirements; and mechanistic representation of the immune response and diseases.
Prediction of voluntary feed intake
An accurate prediction of feed intake is the most critical step in all animal models for realistic determination of the efficiency of nutrient utilisation and of animal performance. Many different concepts and approaches have been used to model feed intake of animals (Black 2009). These include (1) simple algorithms fitted to experimental data and based largely on animal weight and the available energy content and/or composition of the diet (Poppi 2008; Black 2009); (2) maximum efficiency of oxygen utilisation with animals ceasing to eat when the intake of net energy per litre of oxygen consumed is maximised (Tolkamp and Ketelaars 1992); (3) minimal discomfort theory where feed intake corresponds with the minimal total physical and metabolic discomfort experienced by an animal (Forbes 2007, 2009); (4) continual minute by minute prediction of the energy and protein status from metabolite concentrations in blood and of rumen fill in cattle relative to pre-determined limits using a binary system to initiate and terminate feeding bouts (Nagorcka et al. 2004); (5) the potential-constraint theory where an animal will eat to satisfy its total energy needs determined by its genetics and physiological state unless constrained by various dietary, environmental, health or social factors (Black et al. 1986; Nyachoti et al. 2004; Poppi et al. 1994); and (6) first limiting nutrient theory where animals eat to meet their requirements for the first limiting nutrients in the feed (Emmans 1981; Kyriazakis and Emmans 1998).
Although there are limitations to each of these approaches for predicting voluntary feed intake, the potential-constraint and first limiting nutrient concepts appear to be the most effective over a wide range of situations (Black 2009; Ferguson 2014). However, these have limitations. First, Forbes (2009) criticised the approach of a single, but changeable feedback mechanism limiting feed intake, because it does not fit with physiology concepts of how an animal functions. Second, whenever the model iteration interval is greater than a few minutes, being 1 day in many of the models mentioned, the commencement and cessation of feeding bouts cannot be predicted nor can the impact be predicted from variations within a day as occurs with changes in pasture availability or with changes in climatic conditions. These criticisms have been overcome by an approach similar to that used by Nagorcka et al. (2004) where the concentration of crucial metabolites controlling hunger and satiety within the blood is predicted on a minute by minute basis. Similarly, several models using the first limiting nutrient approach have used hourly rather than daily integration intervals (Ferguson 2014; Gous 2014). However, no current animal model truly represents the biological control of feed intake. There is an opportunity to develop a more comprehensive mechanistic model of voluntary feed intake in animals on the basis of current understanding of the metabolic and physical regulation of intake. This could be achieved by describing essential metabolic pathways, changes in metabolite pool sizes and physical, neural and endocrine interactions in a model with short iteration intervals.
Voluntary feed intake is controlled by the following two main processes: (i) rate of removal of digesta from the gastrointestinal tract (GIT) through changes in transit time and in the rate of digestion and absorption of dietary constituents; and (ii) brain-controlled hunger and satiety responses resulting from the physical consumption of feed, absorption of products of digestion and metabolites produced from subsequent biochemical reactions. Although the broad mechanisms for feed-intake control are similar for ruminants and monogastric animals (Roche et al. 2008; Black et al. 2009), understanding of these mechanisms is more advanced for the latter group of animals. The processes that could be modelled for monogastric animals, particularly the pig, are summarised below and described in detail by Black et al. (2009).
Feed intake is stimulated in monogastric animals as the rate of passage of digesta increases, particularly through the stomach and small intestine. Physical characteristics of the diet that cause mild distension stimulate the rate of stomach emptying and propagative peristaltic contractions in the GIT and increase feed intake. However, excessive distension inhibits these responses, slows rate of passage and induces satiety via the vagus nerve–hindbrain–forebrain reflex. Increasing the amount of indigestible fibre, or other undigested particles, in a diet for pigs can increase or decrease rate of passage and feed intake depending on the amount of fibre and size of particles. Small indigestible fibre particles are less effective for stimulating rate of passage than are medium-sized particles, which in turn, are more effective that very large particles. Excessive distension of the GIT and reduced rate of passage can also be caused by diets with high soluble fibre content that increases digesta viscosity. Although precise details of the interactions between particle size, viscosity and gut anatomy are not fully understood, development of components of the model based on the principles of rheology would allow these relationships to be explored and to identify whether more experiments are required to clarify the interactions.
Nutrients and their metabolites, present in the GIT and absorbed, control feed intake over the short and long term through the direct or indirect release of endocrines and their interaction with local and central neural processes. Consumed carbohydrates, fats and proteins that are partially digested by mammalian and microbial enzymes directly affect the release of hormones from the (GIT) and pancreas (peptide tyrosine tyrosine (PYY), glucogon-like peptide-1 (GLP-1), oxyntomodulin and apolipoprotein A-IV). The quantitative and temporal release of these hormones depends on the composition of nutrients consumed, their site and extent of digestion and products released within the GIT. They appear not to be released if the ingredients are indigestible, as these indigestible particles appear to simply stimulate the rate of digesta passage. The nutrient-released hormones act to slow the rate of stomach emptying, reduce the frequency, pressure and progressive distance of peristaltic contractions in the small intestine and reduce feed intake. The action of these hormones has been defined as the ileal brake (Spiller et al. 1984). Hence, rate of passage can be stimulated by mild distension, but inhibited by excessive distension and the presence of undigested nutrients near the terminal ileum and colon. The nutrient-stimulated hormones also act through the vagal nervous system or directly on specific regions of the brain to have longer-term effects on reducing feed intake.
In animal nutrition models, it has not been traditional to model the release of endocrines, interactions between physical distension and neural control of functions. However, some aspects of these mechanisms have been undertaken in models of human metabolic control and should now be attempted in animal systems (Dalla Man et al. 2007; Farhy 2010; Chambers et al. 2013). Furthermore, recent research shows that the rate of digestion of grains and pulses in the small intestine of pigs is closely related to the diffusion rates of amylolytic and protease enzymes into the feed particles (Al-Rabadi et al. 2009, 2011a, 2011b; Mahasukhonthachat et al. 2010a, 2010b; Dhital et al. 2010; Tinus et al. 2012). The rate of enzyme diffusion appears to be influenced by several factors including particle size, physical and chemical characteristics of the grain such as degree of compaction, hardness, endosperm cell-wall integrity, gelatinisation, retrogradation of starch and surface hardening of pellets. Amylase diffusion rates were found to be eight times slower than diffusion rates of water for barley grain and 13 times slower for sorghum (Al-Rabadi et al. 2009). Enzyme diffusion rate and digestion rate has been shown to decrease with the square of grain particle size, with a doubling of particle size reducing starch digestion rate four-fold (Al-Rabadi et al. 2009). These concepts relating enzyme diffusion rates to digestion rate of feed ingredient components, in combination with estimates of the rate of gastric emptying and peristaltic activity within the small intestine determining rate of digesta passage, could readily form the basis for mechanistic simulation of the effects of digestive processes on feed intake.
Such a modelling approach would enable quantitative prediction of nutrients digested in both the small and large intestines. Having the capacity to distinguish between small and large intestine digestion is important in monogastric animals to estimate the composition of the nutrients absorbed and to predict the loss of energy from the animal as heat of fermentation or in methane and voided gut microbes.
Long-term control of feed intake, energy metabolism, body composition and bodyweight is under the influence of two opposing energy monitoring systems within the body. These are adenosine monophosphate-activated protein kinase (AMPK) and mammalian target of rapamycin (mTOR), which act both peripherally and centrally within the hypothalamus. AMPK is activated by metabolic or environmental conditions that deplete cells of ATP by monitoring the adenosine monophosphate (AMP) : ATP ratio. AMPK inhibits ATP-consuming pathways and stimulates ATP-producing catabolic pathways through the regulation of key metabolic enzymes involved in lipid, carbohydrate and protein metabolism. Within the hypothalamus, AMPK regulates the concentration of a key intake controlling metabolite, malonyl-CoA. Low energy status and high AMPK activation also lead to inactivation of mTOR which, contrary to AMPK, reflects high energy status of an animal. Activation of mTOR within the hypothalamus is also controlled by insulin and leptin. Basal insulin and leptin concentrations are directly proportional to the amount of fat, or adiposity status, of an animal. Malonyl-CoA and mTOR have a central role in controlling expression of the hypothalamic melanocortin system, which has a major role in regulating feed intake and energy expenditure. Low energy, or adiposity status, results in low concentrations of malonyl-CoA and low activation of mTOR, which stimulates the expression of melanocortin system orexigenic peptides, neuropeptide tyrosine and agouti-related peptide, and reduces the expression of anorexigenic peptides, proopiomelanocortin, α-melanocyte-stimulating hormone and cocaine and amphetaminerelated transcript, thereby increasing intake and reducing energy expenditure. Conversely, high energy status with high concentrations of malonyl-CoA and high activation of mTOR, reduce the expression of the orexigenic peptides, increase the expression of anorexigenic peptides and reduce feed intake, while increasing energy expenditure.
These perceived mechanisms of interactions between current and long-term energy status and eating bouts of animals could be readily simulated. The modelling could be either at a metabolic level similar to that described above or at a simpler level based on a prediction of current energy status of the animal through, for example, blood metabolite concentrations as used by Nagorcka et al. (2004), in combination with an ongoing estimate of current adiposity relative to a genetic potential.
Feed intake potential in diet formulation
Diet-formulation software used to combine available ingredients to meet nutrient requirements of animals at least cost does not consider the effects of the ingredients on feed intake. The value of a diet as an energy source to an animal depends on the total amount of energy made available for metabolism in megajoules per day. Total energy available to an animal is determined by the amount digested along the whole digestive tract, when accounting for energy losses from the animal associated with microbial digestion through heat of fermentation and methane, (energy content, MJ/kg) and the total amount of the diet consumed (kg/day). Animal performance and productivity is driven by the intake of metabolisable energy.
The digestible, metabolisable or net energy content of each ingredient is used in current feed-formulation software to predict the combination of ingredients that will meet a specified energy content of the formulated diet. Results from a large research program in Australia investigating the energy value of cereal grains for different livestock types (Black 2014), show there is little relationship between the available energy content of grains and voluntary feed intake when the grains are incorporated into diets. The correlation coefficients relating diet intake to digestible energy (DE) content of grains were 0.07, −0.34, 0.39 and −0.24 for cattle, pigs, broiler chickens and layers respectively. The lack of a clear relationship between DE content of grains and intake is further illustrated by the results from Cadogan et al. (1999), where the DE content of five different cultivars of wheat fed to young pigs ranged only from 14.39 to 14.96 MJ/kg dry matter (4%), but feed intake ranged from 389 to 691 g/day (78%, Table 1). These low and negative correlations illustrate that formulating diets with high or low DE content does not guarantee high or low total energy intakes. The poor relationship between DE content and intake reinforces the information outlined in the previous section of this paper, which suggests different characteristics of diets determine digestibility and intake.

|
Thus, the effect of an ingredient added to a diet on feed intake needs to be incorporated into least-cost feed-formulation software. There are two possible ways this could be achieved. First, an intake value could be applied to each ingredient and ingredients combined to maximise this value at least cost. For example, an apparent metabolisable energy (AME) intake index has been applied to ~300 cereal grains, including wheat, barley, triticale, sorghum, maize and rice fed to broiler chickens (Black et al. 2014). The index was derived by measuring the AME content (MJ/kg) and feed intake (kg/day) in 22-day-old broiler chickens to calculate AME intake (MJ/day). The AME intake for each grain was then divided by the highest AME intake value to provide an AME intake index with theoretical values from 0 to 100. The index value was used rather than the MJ/day intake value because the latter is not constant and changes each day as a chicken grows. The index provides a constant estimate of the relativity between grain samples in the amount eaten when incorporated into a diet. Near-infrared spectroscopy calibrations have been developed to predict the AME intake index value for any cereal grain (Black et al. 2014). Similar calibrations have been developed for predicting the DE intake index for growing pigs.
As cereal grains represent from 60% to 70% of diets used in commercial pig and poultry enterprises, application in feed formulation software of an intake index value to cereal grains alone would be a valuable method for taking some account of the effect of grain combinations on likely feed intake of animals. However, as illustrated in the previous section, the addition of other ingredients that alter the rate of passage of digesta, such as indigestible fibre or components that change digesta viscosity, can have marked effects on feed intake. Hence, a second approach would be to imbed a mechanistic model of feed intake within the feed-formulation software to calculate the impact of all ingredient combinations on feed intake. Algorithms that would maximise intake while supplying other specified nutrients at least cost would need to be incorporated into the feed formulation software. This would not be a trivial task, but is a logical extension from development of mechanistic models of feed intake and putting them into day-to-day use.
Methyl-donor requirements
The addition of a methyl group to metabolites and other compounds within the body is essential for maintenance of life within animals. Over 300 methylation reactions have been identified (Brosnan and Brosnan 2006). Methylation is necessary for many functions, including the following: biosynthesis of creatine, phosphatidylcholine and adrenalin; metabolite transport across cell membranes; DNA function and gene expression; hormonal signalling of insulin, growth hormone and corticosteroids; neurotransmission; immune function; muscle contraction; cell growth; protein synthesis; cell membrane integrity; removal of toxins and oxygen free radicals; and others (Brosnan et al. 2007; Obeid 2013). Methylation of DNA has an important role in epigenetics and the translation of gene expression across generations (Niculescu 2012). Abnormal methylation, either hypo- or hypermethylation, is associated with numerous disorders, including embryonic death, neural-tube dysfunction, low cognitive ability, diabetes, cardiovascular disorders, Alzheimer’s disease, fatty liver syndrome, osteoporosis, low immunity, cancer, osmotic stress and others (Cronjé 2008; Obeid 2013).
Although the methyl group is a simple carbon–hydrogen molecule, CH3, it has long been recognised that all methyl groups are initially derived from the diet (Anon 1947). Many compounds contain methyl groups, but methyl donors are unique in that the methyl group is attached either to a sulfur or nitrogen molecule. Despite the essential role of methyl groups in animal metabolism and their need to be supplied from the diet, animal nutrition specialists have not included methyl groups in diet formulation software, nor their metabolism within simulation models.
Maintenance of methyl groups within an animal is controlled through the methionine cycle. The control of the methionine cycle has been widely studied and is now well understood (Mudd et al. 2007; Williams and Schalinske 2007; Cronjé 2008). The process is summarised in Figs 1 and 2. Methionine is converted to S-adenosylmethionine (SAM) via two isomers of the enzyme methionine adenosyl transferase (MAT I, MAT III). These interacting enzymes maintain the concentration of methionine, and therefore SAM, within close limits despite wide fluctuations in methionine supply. SAM is responsible for the transfer of methyl groups to other compounds within the body, which results in the formation of S-adenosylhomocysteine (SAH). SAH is converted to homocysteine (HCY) via SAH hydrolase in a reversible reaction, which favours the synthesis of HCY unless there are perturbations to the cycle. HCY concentrations are kept low by the irreversible transsulfuration of HCY to cystathione and then to cysteine, which is used for the synthesis of several essential compounds including glutathione, taurine, coenzyme A and proteins. The conversion of HCY to cystathione requires vitamin B6. HCY is also converted back to methionine to complete the methionine cycle with methyl groups coming either from 5-methyl tetrahydrofolate or from betaine. Vitamin B6 and B12 are required as cofactors in the folate cycle which provides the methyl group for one reaction converting HCY back to methionine. The folate cycle depends on a supply of dietary folate. Similarly, when betaine is used for transmethylation of HCY to methionine, betaine is required in the diet or can be synthesised from dietary choline.
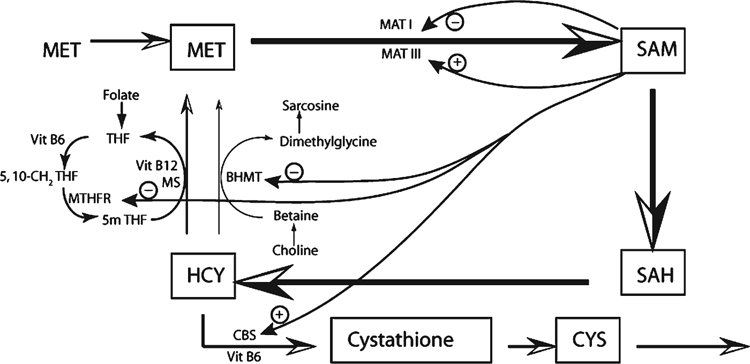
|
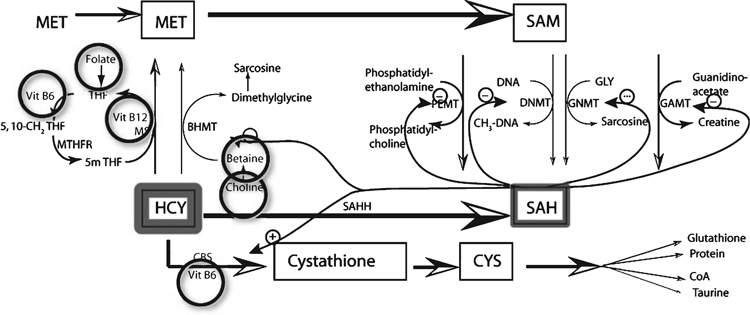
|
The methionine cycle is normally under precise regulation to maintain constant supply of methyl groups to perform the many reactions for which they are needed. However, there must be an optimum supply from the diet of methionine, folate, betaine, choline and vitamin B6 and B12 to maintain this equilibrium. A deficiency of any one of methionine, folate, betaine and choline can be partially compensated for by the others, but the cycle is readily perturbed if dietary provision of these compounds and the cofactors vitamin B6 and B12 are not optimal. Perturbation of the cycle results in excess concentrations of HCY (Obeid 2013), with many negative effects on metabolic processes in an animal and a resultant lowering of production and health status.
Several mathematical models of the methionine cycle have already been developed and used to explore circumstances in human nutrition and health (Reed et al. 2004, 2006, 2008; Prudova et al. 2005; Nijhout et al. 2006). There is an opportunity for animal scientists to further develop models of the methionine cycle and to quantify the need for transmethylation reactions under a range of genetic and environmental situations. The ultimate objective from developing such models would be prediction of the optimal amount of each of the dietary components (methionine, cysteine, folate, betaine, choline, vitamin B6 and vitamin B12) needed for predetermined rates of animal production for animals varying in genetic background and in different environments. The circumstances that lead to either hypo or hypermethylation of DNA and the consequences for epigenitic effects may be a predicted outcome from such mechanistic models. Furthermore, since these models could predict precise dietary requirements for all components needed for full functionality of the methionine cycle, these requirements could then be incorporated into diet formulation software. This long-neglected area of animal nutrition, where the dietary need for methyl donors has not been considered, would be addressed.
Mechanistic representation of disease
Stimulation of the immune response associated with high microbial load and pathogens has a major impact on the performance of intensively reared animals. Commonly, the performance of commercially raised pigs is ~20% less than for pigs grown in ideal environments (Black et al. 2001). Although group penning contributes to this decrease in performance, a major effect is through stimulation of the immune system. Similarly, chickens reared in a germ-free environment were shown to grow 18% faster and have 11% greater feed conversion efficiency than those raised in a commercial environment (Muramatsu et al. 1988).
Diseases and immune stimulation affect several physiological functions of animals, including feed intake, oxygen exchange rate, efficiency of energy utilisation, body protein synthesis and catabolism, body temperature control and tolerance to heat stress. Klasing (2007) estimated that total lysine requirements of chickens increased by 7–10% in association with upregulation of the immune system. The major contributors to the increase in lysine requirements were hypertrophy of the liver and production of acute-phase proteins. The acute-phase proteins also contain higher proportions of cysteine than do muscle proteins and cysteine requirements have been estimated to increase by 7% during immune stimulation. Several measurements of oxygen consumption in humans with sickle cell disease (Borel et al. 1998) or other forms of trauma (Roe and Kinney 1965) suggest that fever increases metabolic rate by ~10–15%, with most of the increase in energy expenditure being due to increases in the rate of protein turnover associated with infection.
The effects of disease have not been incorporated into many models developed for predicting animal growth, except in a simple form. For example, in pig models, Moughan (1995) incorporated the overall effect of the environment, including disease, by reducing potential protein deposition to an ‘operational maximum’ rather than using the ‘genetic maximum’. Similarly, for the model of Black et al. (1986), it is recommended that the potential rate of protein deposition and feed intake are depressed, while maintenance requirement is increased when simulating the effects of disease (Mullan et al. 1994). However, recognition of the importance of diseases in commercial pig production has resulted in several concerted efforts to develop approaches for simulating the effects of diseases on feed intake and performance within pig models (Sandberg et al. 2006; Black 2009; Kyriazakis and Doeschl-Wilson 2009).
These more detailed approaches for modelling disease assume that there is usually a lag between the time of infection and discernable physiological responses; the magnitude of the responses depends on the severity of the disease as determined by the pathogen load and virulence; there may or may not be a recovery phase, depending on the disease and its severity; recovery in the physiological function may or may not reach pre-infection levels; time to recovery depends on nutritional status of the animal; the magnitude of the response is influenced by pig genotype; and animals previously infected with a specific disease may be immune to further infection or have a diminished response. Many of these concepts are well developed by Sandberg et al. (2006) in relation to predicting the effects of disease on feed intake. However, more effort is required to develop parameters for the algorithms for each of the major diseases affecting pigs or other animals before they can be used effectively in practical models.
Future application of models
Value and limitations of models for practical decision making
Despite the enormous potential benefits that should come to practical agriculture through the integration of fundamental scientific knowledge, simulation models have had limited success in helping everyday farm management (Newman et al. 2000; Becu et al. 2008; Ferguson 2014; Rivera-Torres 2014). The most successful models have been those around which business decisions depend, as illustrated by the almost universal use of diet formulation software by the intensive animal industries. Furthermore, some of the more complex models, although not used directly by farm managers, have had a major impact on understanding and have significantly influenced farm practice. Keating and McCown (2001) provided an example of a complex pest-control model that was used to set simple rules on when to spray or not spray and these rules are now generally applied by farmers. Similarly, the pig model described by Black et al. (1986) showed that, provided humidity was less than 90%, maintenance of wet skin for evaporation would prevent heat stress and this prediction led to the introduction of spray cooling systems within Australian piggeries from the late 1980s.
There are several important reasons for failure of most of simulation models to have a significant impact on decision making at the enterprise level and to influence farm profitability. Many systems have been developed by scientists without close knowledge of the decisions that are made on farms or businesses. Their primary purpose was frequently to better understand the biological and physical interactions of a system. The earlier detailed mechanistic models often addressed many biological interactions in great detail, but did not include specific components that relate to the economic decisions that need to be made at the business level. There is clear evidence that the most successful models for field application have involved a close association during development between the model builders and end users (Ferguson 2014). Successful adoption is improved greatly when the emphasis of model development is on its application as well as on science. However, even those animal models that were constructed in consultation with end users and include integrated diet formulation software, profit optimisation, cash flow predictions and expert systems to interpret results (Black et al. 1993), are generally not used consistently to make day-to-day enterprise decisions.
Many animal models are complex and require a great deal of time to understand how they operate and the details of their underlying concepts. Most models require a large number of inputs to run the simulations. This information, such as temperature and humidity changes, air flow rates, genotype description, initial weights, health status, and others, is often not readily obtained at the enterprise level. Finally, most enterprises do not take measurements of farm productivity in sufficient detail to allow the accuracy of the model outputs to be evaluated. A survey of the Australian dairy industry found that farmers and their consultants believe they can rarely afford the time for these activities and are often unconvinced there will be an increased return in profit from the effort involved (Black 2005). There is a perception among these groups that many biological relationships in agricultural systems have what is known as ‘flat’ response curves and payoff functions (Pannell 2004). The consequence of these flat functions is that there is a wide range over which inputs can vary, without major effects on profitability. Thus, there can be a wide margin for error in the actual inputs used with little consequence on performance, profitability or risk. Farmers, therefore, frequently do not see any major difference in profitability when inputs are optimised compared with decisions that are ‘more-or-less’ correct. An important application of simulation models is to identify which response surfaces are not flat and where small changes in inputs can have marked effects on productivity and profitability.
Decision-making process
Most models are known as ‘hard’ systems and deal only with the biophysical aspects of animal enterprises. However, decision making includes ‘soft’ systems components relating to personal and social factors that are rarely taken into account during model development (Newman et al. 2000). The following five steps in decision making have been recognised: (1) appraising the challenge and identifying the problem; (2) surveying the alternative solutions; (3) weighing the advantages and disadvantages of the alternatives; (4) deliberating about commitment to the decision; and (5) taking action (Robinson 2004). All five phases regularly present difficulties to decision makers, yet most animal models assist with only phases (2) and (3). For many enterprise managers, the challenge or problem is not recognised. When the problem is recognised, managers frequently would like someone else to use the simulation model to provide the quantitative information relating to phases (2) and (3) and then allow them to make the final decisions in relation to their own specific goals and aspirations.
Ferguson (2014) listed the following five factors that he believes are essential for the adoption of animal models by enterprises: (1) all significant stakeholders are part of the model design and development process; (2) foster a modelling culture in the enterprise; (3) ensure robust scientific theory and biology within the model with flexibility to add new components as required; (4) include a capacity for the model to optimise management strategies that enhance profit; and (5) spend time to ensure that customers gain confidence in the model for decision making. Although each of these points is important, ongoing commitment from the model ‘champions’ is required to ensure its continuing application within the enterprise. An additional component is required if animal models are to be adopted and continuously used for day-to-day decision making in commercial enterprises – the models must fit seamlessly into and become an essential part of the enterprise management system.
Integration of models into farming systems for real-time decision making
Electronic measurement, interpretation and control of industrial manufacturing are common practice and are being incorporated into animal enterprises through precision livestock-farming systems (Wathes et al. 2008; Banhazi et al. 2012; Pomar et al. 2014). Detailed animal simulation models should become an integral part of such systems, particularly for intensive livestock industries where variation among individual animals contributes to major inefficiencies in resource use and limit enterprise profitability. Methods for integrating pig models into precision farming systems have been described in recent years (Banhazi and Black 2009, 2011; Banhazi et al. 2012; Hauschild et al. 2012; van Milgen et al. 2012; Pomar et al. 2014). Although concepts vary, the principles involve the use of existing or developing electronic technologies to identify individual animals, measure important environmental variables, monitor individual animal weight and body condition, monitor individual or herd health status, as well as control feed composition and feed intake for each animal. Models will run in real time with a separate simulation for each pig in the group. The model will become integral to day-to-day management by: (1) automatically combining available diets to optimise amino acid content for individual pigs depending on relative prices of ingredients and price penalties for fat pigs; (2) determining whether ambient temperature is above or below thermoneutral and the relative costs and benefits from altering environmental temperature and wind speed leading to automatic environment control; (3) identifying whether pigs are under- or over-stocked and the economic benefit from adjusting stocking rate; (4) manipulating feed supply to each pig to ensure optimum growth rate and body composition for meeting specific buyer pricing regimes to maximise profit; and (5) selling individual pigs at a time that maximises enterprise returns.
Animal simulation models that integrate current relevant knowledge are envisaged to become an indispensible and virtually invisible part of the management of future intensive animal enterprises. Electronically measured data will be incorporated into model simulations, the data interpreted through the model and used to control feeding, the environment and sale of animals in real time to maximise profit.
Conclusions
Animal simulation models have progressed greatly since the first use of mathematical equations to describe animal functions 100 years ago. Most of the current animal-nutrition models represent animal systems well and several have been used to successfully predict outcomes that had not previously been observed. Nevertheless, there are opportunities for further development of specific aspects of animal models. These include a more mechanistic representation of the control of feed intake, prediction of methyl-donor requirements and representation of the methionine cycle and methylation processes, and more mechanistic representation of individual animal diseases and the effects of microbial loads within commercial animal environments. Few models have been used for day-to-day decision making on farm, partly because of the: complexity of the models; difficulty in obtaining accurate information needed as model inputs; and flat pay-off response curves for many agricultural systems. However, a strong future for animal models is envisaged when they will be incorporated into precision livestock-farming systems, run real time for individual animals and will be used to electronically control operations within an enterprise.
References
Adelson DL (1991) Experimental tests of an initiation model. In ‘Workshop on wool biology’. (Ed. PI Hynd) pp. 49–56. (Australian Wool Corporation: Melbourne)Al-Rabadi GJS, Gilbert RG, Gidley MJ (2009) Effect of particle size on kinetics of starch digestion in milled barley and sorghum grains by porcine alpha-amylase. Journal of Cereal Science 50, 198–204.
| Effect of particle size on kinetics of starch digestion in milled barley and sorghum grains by porcine alpha-amylase.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1MXhtVKlsr3O&md5=13113d36f27ad8a3f7d9e7c74270c5c7CAS |
Al-Rabadi GJS, Torley PJ, Williams BA, Bryden WL, Gidley MJ (2011a) Effect of extrusion temperature and pre-extrusion particle size on starch digestion kinetics in barley and sorghum grain extrudates. Animal Feed Science and Technology 168, 267–279.
| Effect of extrusion temperature and pre-extrusion particle size on starch digestion kinetics in barley and sorghum grain extrudates.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXhtVKksLfM&md5=2a3c248f7c14bb3a0fa72daeab2bff92CAS |
Al-Rabadi GJS, Sopade PA, Gidley MJ (2011b) Particle size of milled barley and sorghum and physico-chemical properties of grain following extrusion. Journal of Food Engineering 103, 464–472.
| Particle size of milled barley and sorghum and physico-chemical properties of grain following extrusion.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXjsVeqtw%3D%3D&md5=9a254dc842dad95b485ed6cfc054c49eCAS |
Anon. (1947) Present knowledge of methyl groups in nutrition. Nutrition Reviews 5, 131–134.
ARC (Agricultural Research Council) (1965) ‘The nutrient requirements of farm livestock. No 2. Ruminants.’ (Agricultural Research Council London: London)
Baldwin RL (1995) ‘Modelling ruminant digestion and metabolism.’ (Chapman & Hall: London)
Baldwin RL, Black JL (1979) ‘Simulation of the effects of nutritional status and physiological status’. Research Laboratories Technical Paper No. 6. (CSIRO Publishing: Melbourne)
Baldwin RL, Koong LJ (1980) Mathematical modelling in analysis of ruminant digestive function: philosophy, methodology and application. In ‘Digestive physiology and metabolism in ruminants’. (Eds Y Ruckerbusch, P Thivend) pp. 251–268. (MTP Press: Lancaster, UK)
Baldwin RL, Smith NE (1971) Application of simulation modelling techniques in analysis of dynamic aspects of animal energetics. Federation Proceedings 30, 1459–1465.
Baldwin RL, France J, Gill M (1987a) Metabolism of the lactating cow: 1. Animal elements of a mechanistic model. The Journal of Dairy Research 54, 107–131.
| Metabolism of the lactating cow: 1. Animal elements of a mechanistic model.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2sXkvFWhsg%3D%3D&md5=8442cb40efc705f11b46c7f5dcf45b46CAS | 3819150PubMed |
Baldwin RL, Thornley JHM, Beever DE (1987b) Metabolism of the lactating cow: 2. Digestive elements of a mechanistic model. The Journal of Dairy Research 54, 77–105.
| Metabolism of the lactating cow: 2. Digestive elements of a mechanistic model.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2sXkslKitA%3D%3D&md5=43d67267723bd391d3469df7c55f71aaCAS | 3819156PubMed |
Baldwin RL, France J, Beever DE, Gill M, Thornley JHM (1987c) Metabolism of the lactating cow: 3. Properties of mechanistic models suitable for evaluation of energetic relationships and factors involved in the partition of nutrients. The Journal of Dairy Research 54, 133–145.
| Metabolism of the lactating cow: 3. Properties of mechanistic models suitable for evaluation of energetic relationships and factors involved in the partition of nutrients.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaL2sXkvFWhsw%3D%3D&md5=53889228d65f8fab5fc050ac3e0b5f6fCAS | 3819152PubMed |
Banhazi TM, Black JL (2009) Precision livestock farming: a suite of electronic systems to ensure the application of best practice management on livestock farms. Australian Journal of Multi-Disciplinary Engineering 7, 1–14.
Banhazi TM, Black JL (2011) The precision livestock farming journey: from a scientific dream towards commercial reality. In ‘Multi-disciplinary approach to acceptable and practical precision livestock farming foe SME’s in Europe and world wide’. (Eds IG Smith, H Lehr) pp 192–207 (European Commission: Halifax, UK)
Banhazi TM, Lehr H, Black JL, Crabtree H, Schofield P, Tscharke M, Berckmans D (2012) Precision livestock farming: an international review of scientific and commercial aspects. International Journal of Agricultural and Biological Engineering 5, 1–9.
Bastianelli D, Sauvant D (1998) Digestion absorption and excretion. In ‘A quantitative biology of the pig’. (Ed. I Kyriazakis) pp. 249–273. (CAB International: Wallingford)
Baudracco J, Lopez-Villalobos N, Holmes CW, Comeron EA, Macdonald KA, Barry TN (2013) Dairy: a dynamic and stochastic whole-farm model that predicts biophysical and economic performance of grazing dairy systems. Animal 7, 870–878.
| Dairy: a dynamic and stochastic whole-farm model that predicts biophysical and economic performance of grazing dairy systems.Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BC3s3js1CqtQ%3D%3D&md5=596b9fe963eeab75f88e61c6764bcd5fCAS | 23257214PubMed |
Becu N, Neef A, Schreinemachers P, Sangkapitux C (2008) Participatory computer simulation to support collective decision-making: potential and limits of stakeholder involvement. Land Use Policy 25, 498–509.
| Participatory computer simulation to support collective decision-making: potential and limits of stakeholder involvement.Crossref | GoogleScholarGoogle Scholar |
Black JL (1995) Approaches to modelling. In ‘Modelling growth in the pig’. (Eds PJ Moughan, MWA Verstegen, MI Visser-Reyneveld) pp. 11–22. (Wageningen Pers: Wageningen, The Netherlands)
Black JL (2005) Review of the needs and availability of suitable models and decision support tools for the on-farm portfolio of Dairy Australia and its industry clients. Final report. Dairy Australia, Melbourne.
Black JL (2009) Models to predict feed intake. In ‘Voluntary feed intake in pigs’. (Eds D Torrallardona, E Roura) pp. 323–351. (Wageningen Academic Publishers: Wageningen, The Netherlands)
Black JL (2014) Cereal grains as animal feed. In ‘Encyclopaedia of food grains. Vol. 3’. (Eds H Corke, K Seetharaman, CW Wrigley) In Press. (Elsevier Publishing: Oxford, UK)
Black JL, Banhazi TM (2013) Economic and social advantages of precision livestock farming in the pig industry. In ‘The proceedings of the 6th European conference on precision livestock farming’. (Eds D Berckmans, J Vandermeulen) pp. 199–208. (Catholic University of Leuven: Leuven, Belgium)
Black JL, de Lange CFM (1995) Introduction to the principles of nutrient partitioning for growth. In ‘Modelling growth in the pig’. (Eds PJ Moughan, MWA Verstegen, MI Visser-Reyneveld) pp. 33–45. (Wageningen Pers: Wageningen, The Netherlands)
Black JL, Reis PJ (1979) Speculation on the control of nutrient partition between wool growth and other body functions. In ‘Physiological and environmental limitations to wool growth’. (Eds JL Black, PJ Reis) pp. 269–294. (University of New England Publishing Unit: Armidale, NSW)
Black JL, Beever DE, Faichney GJ, Howarth BR, Graham NMcC (1981) Simulation of the effects of rumen function on the flow of nutrients from the stomach of sheep: Part 1. Description of a computer program. Agricultural Systems 6, 195–219.
| Simulation of the effects of rumen function on the flow of nutrients from the stomach of sheep: Part 1. Description of a computer program.Crossref | GoogleScholarGoogle Scholar |
Black JL, Campbell RG, Williams IH, James KJ, Davies GT (1986) Simulation of energy and amino acid utilisation in the pig. Research and Development in Agriculture 3, 121–145.
Black JL, Davies GT, Fleming JF (1993) Role of computer simulation in the application of knowledge to animal industries. Australian Journal of Agricultural Research 44, 541–555.
| Role of computer simulation in the application of knowledge to animal industries.Crossref | GoogleScholarGoogle Scholar |
Black JL, Giles LR, Wynne PC, Knowles AG, Kerr CA, Jones MR, Strom AD, Gallagher NL, Eamens GJ (2001) A review – Factors limiting the performance of growing pigs in commercial environments. In ‘Manipulating pig production VIII’. (Ed. PD Cranwell) pp. 9–36. (Australasian Pig Science Association: Werribee, Vic.)
Black JL, Williams BA, Gidley MJ (2009) Metabolic regulation of feed intake in monogastric mammals. In ‘Voluntary feed intake in pigs’'. (Eds D Torrallardona, E Roura) pp. 189-213. (Wageningen Academic Publishers: Wageningen, The Netherlands)
Black JL, Hughes RJ, Diffey S, Tredrea AM, Flinn PC, Spragg JC, Kim JC (2014) Rapid assessment of feed ingredient quality. In ‘Annual Australian poultry science symposium 25’. pp. 23–30. (The University of Sydney: Sydney)
Blaxter KL (1962) ‘Energy metabolism of ruminants.’ (Hutchinson: London)
Borel MJ, Buchowski MS, Turner EA, Goldstein RE, Flakoll PJ (1998) Protein turnover and energy expenditure increases during exogenous nutrient availability in sickle cell disease. The American Journal of Clinical Nutrition 68, 607–614.
Brody S, Ragsdale AC (1921) The rate of growth of the dairy cow: extrauterine growth in weight. The Journal of General Physiology 3, 623–633.
| The rate of growth of the dairy cow: extrauterine growth in weight.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DyaB3MXhtlaitw%3D%3D&md5=68ffdd1a20ff500c05d5d6bac22f5740CAS | 19871892PubMed |
Brosnan JT, Brosnan ME (2006) The sulphur containing amino acids: an overview. The Journal of Nutrition 136, 1636S–1640S.
Brosnan ME, Edison EE, da Silva R, Brosnan JT (2007) New insights into creatine function and synthesis. Advances in Enzyme Regulation 47, 252–260.
| New insights into creatine function and synthesis.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXhtVOhsbc%3D&md5=1c28c54d8df2d0e14b5e1f769cfe1847CAS | 17335874PubMed |
Bruce JM, Clark JJ (1979) Models of heat production and critical temperature of growing pigs. Animal Production 28, 353–369.
| Models of heat production and critical temperature of growing pigs.Crossref | GoogleScholarGoogle Scholar |
Cadogan DJ, Choct M, Campbell RG, Kershaw S (1999) Effect of new season’s wheat on the growth performance of young male pigs. In ‘Manipulating pig production VII’. (Ed. PD Cranwell) p. 40. (Australasian Pig Science Association: Werribee, Vic.)
Chambers JD Thomas EA Bornstein JC (2013 ) Mathematical modelling of enteric neural motor patterns. Proceedings of the Australian Physiological Society 44 75 84
Cronjé P (2008) The requirements of pigs for methyl groups. Report to the Pork CRC Ltd, Roseworthy, SA.
Dalla Man C, Rizza RA, Cobelli C (2007) Meal simulation model of the glucose-insulin system. IEEE Transactions on Bio-Medical Engineering 54, 1740–1749.
| Meal simulation model of the glucose-insulin system.Crossref | GoogleScholarGoogle Scholar | 17926672PubMed |
de Lange CFM, Marty B, Birkett S, Moral P, Szkotnicki B (2001) Application of pig growth models in commercial production. Canadian Journal of Animal Science 81, 1–8.
| Application of pig growth models in commercial production.Crossref | GoogleScholarGoogle Scholar |
Dhital S, Shrestha AK, Gidley MJ (2010) Relationships between granule size and in-vitro digestibility of maize and potato starches. Carbohydrate Polymers 82, 480–488.
| Relationships between granule size and in-vitro digestibility of maize and potato starches.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXptValtr4%3D&md5=6f92624b457f1f5e07682b146dab5eecCAS |
Dijkstra J, Neal HD, Beever DE, France J (1992) Simulation of nutrient digestion, absorption and outflow in the rumen: model description. The Journal of Nutrition 122, 2239–2256.
Dumas A, Dijkstra J, France J (2008) Mathematical modelling in animal nutrition: a centenary review. The Journal of Agricultural Science 146, 123–142.
| Mathematical modelling in animal nutrition: a centenary review.Crossref | GoogleScholarGoogle Scholar |
Ellis JL, Dijkstra J, Kebreab E, Bannink A, Odongo NE, McBride BW, France J (2008) Aspects of rumen microbiology central to mechanistic modelling of methane production in cattle. Journal of Agricultural Science 146, 213–233.
| Aspects of rumen microbiology central to mechanistic modelling of methane production in cattle.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXjs12kuro%3D&md5=094e65bd32dcf71ad8fcbedc978d1c52CAS |
Ellis JL, Dijkstra J, Bannink A, Parsons AJ, Rasmussen S, Edwards GR, Kebreab E, France J (2011) The effect of high-sugar grass on predicted nitrogen excretion and milk yield simulated using a dynamic model. Journal of Dairy Science 94, 3105–3118.
| The effect of high-sugar grass on predicted nitrogen excretion and milk yield simulated using a dynamic model.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3MXnvFCnsrw%3D&md5=6065edfd12b131a52bcfef171c4f8229CAS | 21605779PubMed |
Emmans GC (1981) A model of the growth and feed intake of ad libitum fed animals, particularly poultry. In ‘Computers in animal production’. (Eds GM Hillyer, CT Whittemore, RG Gunn) pp. 103–110. Occasional Publication No. 5. (British Society of Animal Production: Thames Ditton, UK)
Emmans GC (1989) The growth of turkeys. In ‘Recent advances in turkey science’. (Eds C Nixey, TC Grey) pp. 135–166. (Butterworths: London)
Emmans GC, Fisher C (1986) Problems in nutritional theory. In ‘Nutrient requirements of poultry and nutritional research’. (Eds C Fisher, KN Boorman) pp. 9–39. (Butterworths: London)
Emmans GC, Oldham JD (1988) Modelling of growth and nutrition in different species. In ‘Modelling livestock production systems’. (Eds S Karver, JAM van Arendonk) pp. 13–21. (Kluwer Academic: Dordrecht, The Netherlands)
FAO/WHO (1957) ‘Protein requirements. Nutrition studies. No. 6.’ (Food and Agriculture Organisation of the United Nations: Rome)
FAO/WHO (1965) ‘Protein Requirements. Nutrition studies. No. 37.’ (Food and Agriculture Organisation of the United Nations: Rome)
Farhy LS (2010) Modeling of oscillations in endocrine networks with feedbacks. In ‘Essential Numerical Computer Methods’. (Ed. ML Johnson) pp. 309–336. (Academic Press: Burlington, MA)
Ferguson NS (2006) Basic concepts describing animal growth and feed intake. In ‘Mechanistic modelling in pig and poultry production’. (Eds RM Gous, TR Morris, C Fisher) pp. 22–53. (CAB International: Wallingford, UK)
Ferguson NS (2014) Commercial application of integrated models to improve performance and profitability in finishing pigs. In ‘Nutrition modelling for pigs and poultry’. (Eds NK Sakmoura, R Gous, I Kyriazakis, L Hauschild) In Press. (CAB International: Wallingford, UK)
Forbes JM (2007) A personal view of how ruminant animals control their intake and choice of food: minimal total discomfort. Nutrition Research Reviews 20, 132–146.
| A personal view of how ruminant animals control their intake and choice of food: minimal total discomfort.Crossref | GoogleScholarGoogle Scholar | 19079866PubMed |
Forbes JM (2009) Integration of pre- and post-absorptive factors in feed intake regulation and prediction with particular respect to the pig. In ‘Voluntary feed intake in pigs’. (Eds D Torrallardona, E Roura) pp. 61–86. (Wageningen Academic Publishers: Wageningen, The Netherlands)
France J, Dijkstra J (2000). Scientific progress and mathematical modelling: different approaches to modelling animal systems. In ‘Modelling nutrient utilisation in farm animals’. (Eds JP McNamara, J France, DE Beever) pp. 6–21. (CAB International: Wallingford, The Netherlands)
Garfinkel D (1966) A simulation study of the metabolism and compartmentation in brain glutamate, aspartate, the krebs cycle, and related metabolites. The Journal of Biological Chemistry 241, 3918–3929.
Gous RM (2014) A model to optimise broiler production. In ‘Nutrition modelling for pigs and poultry’. (Eds NK Sakmoura, R Gous, I Kyriazakis, L Hauschild) In Press. (CAB International: Wallingford, UK)
Gous RM, Berhe ET (2006) Modelling populations for purposes of optimization. In ‘ Mechanistic modelling in pig and poultry production’. (Eds RM Gous, C Fisher, T Morris) pp 76–96 (CAB International: Wallingford, UK)
Graham NMcC, Black JL, Faichney GJ, Arnold A (1976) Simulation of growth and production in liveweight change, day by day for sheep of any age. Agricultural Systems 1, 113–138.
| Simulation of growth and production in liveweight change, day by day for sheep of any age.Crossref | GoogleScholarGoogle Scholar |
Hauschild L, Lovatto PA, Pomar J, Pomar C (2012) Development of sustainable precision farming systems for swine: estimating real-time individual amino acid requirements in growing-finishing pigs. Journal of Animal Science 90, 2255–2263.
| Development of sustainable precision farming systems for swine: estimating real-time individual amino acid requirements in growing-finishing pigs.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC38XhtFehsbvI&md5=6f463a256d4b45d68362f4b15b7d27d6CAS | 22287679PubMed |
Huxley JS (1924) Constant differential growth-ratios and their significance. Nature 114, 895–896.
| Constant differential growth-ratios and their significance.Crossref | GoogleScholarGoogle Scholar |
Huxley JS, Teissier G (1936) Terminology of relative growth. Nature 137, 780–781.
| Terminology of relative growth.Crossref | GoogleScholarGoogle Scholar |
Johnston SA, Gous RM (2006) Modelling egg production in laying hens. In ‘Mechanistic modelling in pig and poultry production’. (Eds RM Gous, TR Morris, C Fisher) pp. 188–208. (CAB International: Wallingford, UK)
Keating BA, McCown RL (2001) Advances in farming systems analysis and intervention. Agricultural Systems 70, 555–579.
Kebreab E, Vitti DMSS, Odongo NE, Dias RS, Crompton LA, France J (2008) Modelling phosphorus metabolism. In ‘Mathematical modelling in animal nutrition’. (Eds J France, E Kebreab) pp. 353–369. (CAB International: Wallingford, UK)
Klasing KC (2007) Nutrition and the immune system. British Poultry Science 48, 525–537.
| Nutrition and the immune system.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2sXhtFyrurrK&md5=e7a83065d713367bcd4f46fd6e585852CAS | 17952723PubMed |
Knap PW (1995) Aspects of stochasticity: variation between animals. In ‘Modelling growth in the pig’. (Eds PJ Moughan, MWA Verstegen, MI Visser-Reyneveld) pp. 165–172. (Wageningen Pers: Wageningen, The Netherlands)
Kyriazakis I, Doeschl-Wilson A (2009) Anorexia during infection in mammals: variation and its sources. In ‘Voluntary feed intake in pigs’. (Eds D Torrallardona, E Roura) pp. 307–321. (Wageningen Academic Publishers: Wageningen, The Netherlands)
Kyriazakis I, Emmans GC (1998) Voluntary feed intake and diet selection. In ‘A quantitative biology of the pig’. (Ed. I Kyriazakis) pp. 229–248. (CAB International: Wallingford, UK)
Mahasukhonthachat K, Sopade PA, Gidley MJ (2010a) Kinetics of starch digestion and functional properties of twin-screw extruded sorghum. Journal of Cereal Science 51, 392–401.
| Kinetics of starch digestion and functional properties of twin-screw extruded sorghum.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXmsVeksrg%3D&md5=ff793731ee9cd45ed944d65cfd301221CAS |
Mahasukhonthachat K, Sopade PA, Gidley MJ (2010b) Kinetics of starch in sorghum as affected by particle size. Journal of Food Engineering 96, 18–28.
| Kinetics of starch in sorghum as affected by particle size.Crossref | GoogleScholarGoogle Scholar |
Menzies TJ, Black JL, Dean M, Fleming JF (1990). Combining heuristics and simulation models: an expert system for optimal management of pigs. In ‘AI’88. Proceedings of the Australian joint artificial intelligence conference’. pp. 48–61. (Springer-Verlag: London)
Moughan PJ (1995) Modelling protein metabolism in the pig – critical evaluation of a simple reference model. In ‘Modelling growth in the pig’. (Eds PJ Moughan, MWA Verstegen, MI Visser-Reyneveld) pp. 103–112. (Wageningen Pers: Wageningen, The Netherlands)
Moughan PJ, Smith WC, Pearson G (1987) Description and validation of a model simulating growth in the pig (20–90 kg liveweight). New Zealand Journal of Agricultural Research 30, 481–489.
| Description and validation of a model simulating growth in the pig (20–90 kg liveweight).Crossref | GoogleScholarGoogle Scholar |
Mudd SH, Brosnan JT, Brosnan ME, Jacobs RL, Stabler SP, Allen RH, Vance DE, Wagner C (2007) Methyl balance and transmethylation fluxes in humans. The American Journal of Clinical Nutrition 85, 19–25.
Mullan BP, Davies GT, Cutler RS (1994) Simulation of the economic impact of transmissible gastroenteritis on commercial pig production in Australia. Australian Veterinary Journal 71, 151–154.
| Simulation of the economic impact of transmissible gastroenteritis on commercial pig production in Australia.Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DyaK2czkslSgtw%3D%3D&md5=a181e51fdc61437e605ad49434263b18CAS | 8067950PubMed |
Muramatsu T, Takasu O, Furuse M, Okumura J-I (1988) Effect of diet type on enhanced intestinal protein synthesis by the gut microflora in the chick. The Journal of Nutrition 118, 1068–1074.
Nagorcka BN, Mooney JR (1989) The reaction-diffusion system as a spatial organiser during initiation and development of hair follicle and formation of fibre. In ‘The biology of wool and hair’. (Eds GE Rogers, PJ Reis, KA Ward, RC Marshall) pp. 365–379. (Chapman & Hall: New York)
Nagorcka BN Zurcher EJ (2002 ) The potential gains achieved through access to more advanced/mechanistic models of ruminants. Proceedings of the Australian Society of Animal Production 24 ,455 –461 .
Nagorcka BN, Gordon GLR, Dynes RA (2000) Towards a more accurate representation of fermentation in mathematical models of the rumen. In ‘Modelling nutrient utilisation in farm animals’. (Eds JP McNamara, J France, DE Beever) pp. 37–48. (CAB International: Wallingford, UK)
Nagorcka BN, Charmley E, Duynisveld JL (2004) Using a dynamic model to understand the difference in performance of cattle fed rations based on barley and/or a potato processing by-product. Journal of Animal Science 82, 159 [Abstract].
Newman S, Lynch T, Plummer AA (2000) Success and failure of decision support systems: learning as we go. Journal of Animal Science 77, 1–12.
Niculescu MD (2012) Nutritional epigenetics. ILAR Journal 53, 270–278.
| Nutritional epigenetics.Crossref | GoogleScholarGoogle Scholar | 23744966PubMed |
Nijhout HF, Reed MC, Anderson DF, Mattingly JC, James J, Ulrich CM (2006) Long-range allosteric interactions between the folate and methionine cycles stabilize DNA methylation reaction rate. Epigenetics 1, 81–87.
| Long-range allosteric interactions between the folate and methionine cycles stabilize DNA methylation reaction rate.Crossref | GoogleScholarGoogle Scholar | 17998813PubMed |
Nyachoti CM, Zilstra RT, de Lange CFM, Patience JF (2004) Voluntary feed intake in growing-finishing pigs: a review of the main determining factors and potential approaches for accurate predictions. Canadian Journal of Animal Science 84, 549–566.
| Voluntary feed intake in growing-finishing pigs: a review of the main determining factors and potential approaches for accurate predictions.Crossref | GoogleScholarGoogle Scholar |
Obeid R (2013) The metabolic burden of methyl donor deficiency with focus on the betaine homocysteine methyltransferase pathway. Nutrients 5, 3481–3495.
| The metabolic burden of methyl donor deficiency with focus on the betaine homocysteine methyltransferase pathway.Crossref | GoogleScholarGoogle Scholar | 24022817PubMed |
Oltjen JW, Bywater AC, Baldwin RL, Garrett WN (1986) Development of a dynamic model of beef cattle growth and composition. Journal of Animal Science 62, 86–97.
Oltjen JW, Selk GE, Burditt LG, Plant RE (1990) Integrated expert system for culling management of cows. Computers and Electronics in Agriculture 4, 333–341.
| Integrated expert system for culling management of cows.Crossref | GoogleScholarGoogle Scholar |
Pannell DJ (2004) Flat-earth economics: the far-reaching consequences of flat payoff functions in economic decision making. Paper presented at 48th annual conference of the Australian Agricultural and Resource Economics Society, Melbourne, 11–13 February 2004.
Pomar C, Pomar J, Rivest J, Cloutier L, Letourneau-Montminy M-P, Andretta I, Hauschild L (2014) Estimating real-time amino acid requirements in growing-finishing pigs: towards a new definition of nutrient requirements in growing-finishing pigs? In ‘Nutrition modelling for pigs and poultry’. (Eds NK Sakmoura, R Gous, I Kyriazakis, L Hauschild) In Press. (CAB International: Wallingford, UK)
Poppi DP (2008) The dilemma in models of intake regulation: mechanistic or empirical. In ‘Mathematical modelling in animal nutrition’. (Eds J France, E Kebreab) pp. 121–141. (CAB International: Wallingford, UK)
Poppi DP, Gill M, France J (1994) Integration of theories of intake regulation in growing ruminants. Journal of Theoretical Biology 167, 129–145.
| Integration of theories of intake regulation in growing ruminants.Crossref | GoogleScholarGoogle Scholar |
Preisler HK, Ager AA, Johnson BK, Kie JG (2004) Modeling animal movements using stochastic differential equations. Environmetrics 15, 643–657.
| Modeling animal movements using stochastic differential equations.Crossref | GoogleScholarGoogle Scholar |
Prudova A, Martinov MV, Vitvitsky VM, Ataullakhanov FI, Banerjee R (2005) Analysis of pathological defects in methionine metabolism using a simple mathematical model. Biochimica et Biophysica Acta 1741, 331–338.
| Analysis of pathological defects in methionine metabolism using a simple mathematical model.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD2MXhtVegurjL&md5=ce5c1cd8f58c6f2e76e5ff9f8049e9b0CAS | 15963701PubMed |
Reed MC, Nijhout HF, Sparks R, Ulrich CM (2004) A mathematical model of the methionine cycle. Journal of Theoretical Biology 226, 33–43.
| A mathematical model of the methionine cycle.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD3sXptVers74%3D&md5=488661cbd5cce2b288b3463c602f3314CAS | 14637052PubMed |
Reed MC, Nijhout HF, Neuhouser ML, Gregory JF, Shane B, James SJ, Boynton A, Ulrich CM (2006) A mathematical model gives insights into nutritional and genetic aspects of folate-mediated one-carbon metabolism. The Journal of Nutrition 136, 2653–2661.
Reed MC, Thomas RL, Pavisic J, James SJ, Ulrich CM, Nijhout HF (2008) A mathematical model of glutathione metabolism. Theoretical biology and medical modelling 5:8. Available at http://www.thbiomed.com/content/5/1/8). [Accessed 16 June 2014]
Rigolot C, Espagnol S, Robin P, Hassouna M, Piallat JM, Dourmad J-Y (2010) Modelling of manure production by pigs and NH3, NO2 and CH4 emissions. Part II: effect of animal housing, manure storage and treatment practices. Animal 4, 1413–1424.
| Modelling of manure production by pigs and NH3, NO2 and CH4 emissions. Part II: effect of animal housing, manure storage and treatment practices.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC3cXotVCmtrY%3D&md5=1390d05dd2fb08a646506cabd9a33e37CAS | 22444661PubMed |
Rivera-Torres V (2014) Challenges around the application of poultry models: the case of turkeys. In ‘Nutrition modelling for pigs and poultry’. (Eds NK Sakmoura, R Gous, I Kyriazakis, L Hauschild) In Press. (CAB International: Wallingford, UK)
Rivest J, Bernier JF, Pomar C (2000) A dynamic model of protein digestion in the small intestine of pigs. Journal of Animal Science 78, 328–340.
Robinson B (2004) Learning how to improve the development and application of hard systems tools for farming systems research, development and extension. Abstract, PhD Thesis. University of Western Sydney.
Roche JR, Blanche D, Kay JK, Miller DR, Sheahan AJ, Miller DW (2008) Neuroendocrine and physiological regulation of feed intake with particular reference to domestic ruminant animals. Nutrition Research Reviews 21, 207–234.
Roe CF, Kinney JM (1965) The caloric equivalent of fever. II. Influence of major trauma. Annals of Surgery 161, 140–147.
| The caloric equivalent of fever. II. Influence of major trauma.Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DyaF2M%2FlslWhsw%3D%3D&md5=c4c1d312d8bb7eaaf2828be3e9401653CAS | 14252624PubMed |
Rorres C, Pelletier ST, Smith G (2011) Stochastic modeling of animal epidemics using data collected over three different spatial scales. Epidemics 3, 61–70.
| Stochastic modeling of animal epidemics using data collected over three different spatial scales.Crossref | GoogleScholarGoogle Scholar | 21552370PubMed |
Sandberg FB, Emmans GC, Kyriazakis I (2006) A model for predicting feed intake of growing animals during exposure to pathogens. Journal of Animal Science 84, 1552–1566.
Smouse PE, Focardi S, Moorcroft PR, Kei JG, Forester JD, Morales J (2010) Stochastic modelling of animal movement. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences 365, 2201–2211.
| Stochastic modelling of animal movement.Crossref | GoogleScholarGoogle Scholar | 20566497PubMed |
Spiller RC, Trotman IF, Higgins BE, Ghatei MA, Grimble GK, Lee YC, Bloom SR, Misiewicz JJ, Silk DB (1984) The ileal brake-inhibition of jejunal motility after ilela fat perfusion in man. Gut 25, 365–374.
Stevenson MA, Sanson RL, Stern MW, O’Leary BD, Sujau M, Moles-Benfell N, Morris RS (2013) InterSpread Plus: a spatial and stochastic simulation model of disease in animal populations. Preventive Veterinary Medicine 109, 10–24.
| InterSpread Plus: a spatial and stochastic simulation model of disease in animal populations.Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BC38bos1ygsg%3D%3D&md5=cb7a4c041703c4c0a00815e862475edaCAS | 22995473PubMed |
Thornley JHM (2008) Interesting simple dynamic growth models. In ‘Mathematical modelling in animal nutrition’. (Eds J France, E Kebreab) pp. 89–120. (CAB International: Wallingford, UK)
Thornley JHM, France J (2008) Modelling bovine spongiform encephalopathy. Journal of Agricultural Science 146, 183–194.
| Modelling bovine spongiform encephalopathy.Crossref | GoogleScholarGoogle Scholar |
Thornley JHM, France J (2009) Modelling foot and mouth disease. Preventive Veterinary Medicine 89, 139–154.
| Modelling foot and mouth disease.Crossref | GoogleScholarGoogle Scholar |
Tinus T, Damour M, van Riel V, Sopade PA (2012) Particle size-starch-protein digestibility relationships in cowpea (Vigna unguiculata). Journal of Food Engineering 113, 254–264.
| Particle size-starch-protein digestibility relationships in cowpea (Vigna unguiculata).Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BC38Xpt1SgsLc%3D&md5=9abda9cf8217181674e297e9e7af5770CAS |
Tolkamp BJ, Ketelaars JJMH (1992) Towards a new theory of feed intake regulation in ruminants. 2. Costs and benefit of feed consumption: and optimization approach. Livestock Production Science 30, 297–317.
| Towards a new theory of feed intake regulation in ruminants. 2. Costs and benefit of feed consumption: and optimization approach.Crossref | GoogleScholarGoogle Scholar |
van Milgen J, Valancogne A, Dubois S, Dourmond J-Y, Steve B, Noblet J (2008) InraPorc: a model and decision support tool for nutrition of growing pigs. Animal Feed Science and Technology 143, 387–405.
| InraPorc: a model and decision support tool for nutrition of growing pigs.Crossref | GoogleScholarGoogle Scholar | 1:CAS:528:DC%2BD1cXms1WjsLk%3D&md5=453649f2e8020269351ad476c6b5b9f4CAS |
van Milgen J, Noblet J, Dourmad JY, Labussière G, Garcia-Launay F, Brossard L (2012) Precision pork production; predicting the impact of nutritional strategies on carcass quality. Meat Science 92, 182–187.
| Precision pork production; predicting the impact of nutritional strategies on carcass quality.Crossref | GoogleScholarGoogle Scholar | 1:STN:280:DC%2BC38rnsVensQ%3D%3D&md5=e3f30e03c78eed95a8df00a4c290937cCAS | 22525881PubMed |
Wathes CM, Kristensen HH, Aerts JM, Berckmans D (2008) Is precision farming an engineer’s daydream or a nightmare, an animal’s friend or foe, and a farmer’s panacea or pitfall? Computers and Electronics in Agriculture 64, 2–10.
| Is precision farming an engineer’s daydream or a nightmare, an animal’s friend or foe, and a farmer’s panacea or pitfall?Crossref | GoogleScholarGoogle Scholar |
Whittemore CT (1983) Development of recommended energy and protein allowances for growing pigs. Agricultural Systems 11, 159–186.
| Development of recommended energy and protein allowances for growing pigs.Crossref | GoogleScholarGoogle Scholar |
Whittemore CT, Fawcett RH (1974) Model responses of the growing pig to the dietary intake of energy and protein. Animal Production 19, 221–231.
| Model responses of the growing pig to the dietary intake of energy and protein.Crossref | GoogleScholarGoogle Scholar |
Williams KT, Schalinske KL (2007) New insights into the regulation of methyl groups and homocysteine metabolism. The Journal of Nutrition 137, 311–314.
Wood TB, Yule GU (1914) Statistics of British feeding trials and the starch equivalent theory. Journal of Agricultural Science 6, 233–251.
| Statistics of British feeding trials and the starch equivalent theory.Crossref | GoogleScholarGoogle Scholar |


