Can Popular DFT Approximations and Truncated Coupled Cluster Theory Describe the Potential Energy Surface of the Beryllium Dimer?*
Amir Karton A C and Laura K. McKemmish BA School of Molecular Sciences, The University of Western Australia, Perth, WA 6009, Australia.
B School of Chemistry, University of New South Wales, UNSW Sydney, NSW 2052, Australia.
C Corresponding author. Email: amir.karton@uwa.edu.au
Australian Journal of Chemistry 71(10) 804-810 https://doi.org/10.1071/CH18269
Submitted: 2 June 2018 Accepted: 2 July 2018 Published: 26 July 2018
Abstract
The potential energy surface (PES) of the ground state of the beryllium dimer poses a significant challenge for high-level ab initio electronic structure methods. Here, we present a systematic study of basis set effects over the entire PES of Be2 calculated at the full configuration interaction (FCI) level. The reference PES is calculated at the valence FCI/cc-pV{5,6}Z level of theory. We find that the FCI/cc-pV{T,Q}Z basis set extrapolation reproduces the shape of the FCI/cc-pV{5,6}Z PES as well as the binding energy and vibrational transition frequencies to within ~10 cm−1. We also use the FCI/cc-pV{5,6}Z PES to evaluate the performance of truncated coupled cluster methods (CCSD, CCSD(T), CCSDT, and CCSDT(Q)) and contemporary density functional theory methods (DFT) methods for the entire PES of Be2. Of the truncated coupled cluster methods, CCSDT(Q)/cc-pV{5,6}Z provides a good representation of the FCI/cc-pV{5,6}Z PES. The GGA functionals, as well as the HGGA and HMGGA functionals with low percentages of exact exchange tend to severely overbind the Be2 dimer, whereas BH&HLYP and M06-HF tend to underbind it. Range-separated DFT functionals tend to underbind the dimer. Double-hybrid DFT functionals show surprisingly good performance, with DSD-PBEP86 being the best performer. Møller–Plesset perturbation theory converges smoothly up to fourth order; however, fifth-order corrections have practically no effect on the PES.
Introduction
The beryllium dimer (in the X 1∑+ ground state) is a pathologically multireference weakly bound molecule that has eluded electronic structure methods since the 1960s (see ref. [1] for a comprehensive review of the previous literature).[1–15] The multireference character of this elusive diatomic system stems from the near-degeneracy of the 2s and 2p orbitals of the beryllium atom, which is a highly multireference system on its own right.[10,15] The weak bond in Be2 is due to a mixture of dynamic and static correlation effects.[5] The combination of a pathologically multireference system and a weak binding energy make Be2 a notoriously challenging problem for electronic structure methods. The small bond dissociation energy (BDE) of ~900 cm−1 means that an error of 100 cm−1 ≈ 1 kJ mol−1 (which is the target accuracy of highly accurate composite methods such as W4 theory)[16–20] translates to an error ~10 % in the BDE. In order to achieve a more respectable error of ~1 % in the BDE, one has to calculate the BDE to within ~10 cm−1. In the present work, we define benchmark accuracy as errors of ~1 % from the reference value. The significant multireference character means that high-level ab initio methods have to be employed in conjunction with large basis sets in order to achieve this level of accuracy.
Several recent computational studies investigated the PES of Be2 around the equilibrium bond distance using high levels of theory.[2,3,6] These studies have shown that very high levels of theory as well as secondary energetic contributions (e.g. core-valence, scalar relativistic, and diagonal Born–Oppenheimer corrections) are needed in order to reproduce the experimental energetic, structural, and spectroscopic parameters.
Benchmarking approximate ab initio and density functional theory (DFT) procedures against high-level ab initio data has become an important general field over the past two decades (see for example refs [21–25] for an overview). In this context, it is of interest to examine the performance of truncated coupled cluster (CC) and DFT methods for the challenging potential energy surface (PES) of the Be2 dimer. To this end, we calculate the entire PES of Be2 at the valence full-configuration interaction (FCI) complete basis set (CBS) limit. As there are only four valence electrons, we are able to extrapolate the FCI energy to the CBS limit from the cc-pV5Z and cc-pV6Z basis sets. We use the valence FCI/cc-pV{5,6}Z reference data to evaluate the performance of the following levels of theory for the entire PES of the Be2 dimer:
-
FCI/cc-pVnZ (n = D, T, Q, 5, and 6)
-
HF/cc-pV{5,6}Z, CCSD/cc-pV{5,6}Z, CCSD(T)/cc-pV{5,6}Z, CCSDT/cc-pV{5,6}Z, and CCSDT(Q)/cc-pV{5,6}Z
-
Conventional DFT functionals from each rung of Jacob’s Ladder in conjunction with the cc-pV5Z basis set
-
Double-hybrid DFT (DHDFT) methods as well as standard and modified Møller–Plesset perturbation theory (MPn) methods (n = 2–5) in conjunction with the cc-pV5Z basis set.
Computational Methods
All the ab initio calculations were carried out using the MRCC program suite on the Linux cluster of the Karton group at the University of Western Australia.[26,27] In all cases, the correlation-consistent basis sets of Dunning and coworkers were used.[28–30] Several DFT methods were evaluated for their performance in reproducing the FCI/cc-pV{5,6}Z PES. The cc-pV5Z basis set was used in all the DFT and DHDFT calculations. The considered functionals include: (i) the pure generalized gradient approximation (GGA) functionals BLYP,[31,32] PBE,[33,34] revPBE,[35] B97-D3,[36] and N12[37]; (ii) the hybrid GGAs B3LYP,[31,38,39] B3PW91,[38,40] PBE0,[41] and BHandHLYP[42]; (iii) the hybrid meta-GGAs M06,[43,44] M06-2X,[43,44] M06-HF,[45] PW6B95,[46] and MN15,[47] (iv) the range-separated hybrids LC-BLYP,[48] LC-PBE,[48] LC-wPBE,[48] CAM-B3LYP,[49] and wB97X-D,[50] and (v) the double hybrids[51] B2-PLYP,[52] mPW2-PLYP,[53] B2GP-PLYP,[54] the spin-component-scaled double hybrids DSD-BLYP,[55] DSD-PBEP86,[56] and the parameter-free PBE0-DH functional.[57] In some cases, empirical D3 dispersion corrections[58,59] were included using the Becke–Johnson[60] damping potential as recommended in ref. 36 (denoted by the suffix -D3BJ).
In addition, the performance of Møller–Plesset perturbation theory is evaluated. We consider the MPn methods (n = 2, 3, 4, 5), as well as the MPn.5 methods (n = 2, 3, and 4). The latter are defined as the average of MPn and MPn+1.[61,62] All of the DFT and MPn calculations were performed using the Gaussian 16 program suite.[63]
For all levels of theory, a 95-point potential energy curve was calculated. The single-point energy calculations were carried out at bond distances r = req ± x, where req is the equilibrium bond distance at the valence FCI/cc-pV{5,6}Z level of theory and x is varied at 0.001 Å intervals between x = −0.01 and +0.01 Å, at 0.01 Å intervals between x = −1.00 and +2.00 Å, at 0.02 Å intervals between x = −1.60 and +4.00 Å, and at 0.5 Å intervals between x = +4.0 and +14.0 Å. The absolute energies at all the levels of theory considered are given in Table S1 in the Supplementary Material.
Vibrational transition frequencies were obtained using the Duo computer program.[64] In brief, Duo uses the sinc discrete variable representation (DVR) method to find the direct variational solution to the rotational-less diatomic nuclear motion Schrödinger equation.[65] Natural quintic spline interpolation was used between the data points to provide the full potential energy curve. These calculations used 5001 grid points in the range 4.0–19.0 a.u.; the results provided are converged to within 0.01 cm−1.
Results and Discussion
Basis Set Convergence of the FCI Energy
Let us begin by examining the basis set convergence of the valence FCI energy. The PESs calculated at the FCI/cc-pVnZ levels of theory (n = D, T, Q, 5, and 6) are presented in Fig. 1. Errors in the equilibrium bond distance (Δre) and BDE (ΔDe) as well as squared correlation coefficients (R2) with the FCI/cc-pV{5,6}Z PES are given in Table 1. Inspection of Fig. 1 reveals that the shape of the FCI/cc-pVDZ PES is fundamentally flawed. It exhibits two local minima, a deeper one at re = 4.855 a.u. and a shallow one at approximately re = 8 a.u. Previous studies using more approximate correlated ab initio methods have found that the shallow minimum at large distance is an artefact of the small basis set.[5,12,13] The cc-pVTZ basis set results in the correct shape of the PES; however, the PES is too narrow and the binding energy is underestimated by as much as 231 cm−1. The shape of the FCI/cc-pVQZ PES is closer to that of the FCI/cc-pV{5,6}Z PES; however, it is still visibly narrower and the binding energy is still underestimated by 105 cm−1. It should be pointed out that extrapolating the PES from the cc-pV{T,Q}Z basis set pair, at the same computational cost, results in significantly better performance and reduces the error in the binding energy by an order of magnitude. The cc-pV5Z basis set still results in an appreciable error of 49 cm−1 in the binding energy. Extrapolating the PES from the cc-pV{Q,5}Z basis set pair slightly overcorrects for the deficiencies of the cc-pV5Z basis set and results in a binding energy that is too large by 10 cm−1. The cc-pV6Z basis set still results in an appreciable error in the binding energy of 28 cm−1. In summary, only the cc-pV{T,Q}Z and cc-pV{Q,5}Z extrapolations result in benchmark accuracy.
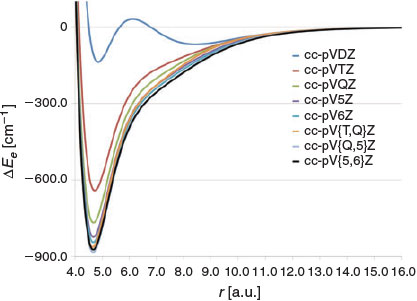
|
In contrast to the binding energy, which converges exceedingly slowly to the basis set limit, re converges much faster. Considering errors smaller than 1 % in the equilibrium bond distance as benchmark accuracy (i.e. errors smaller than 0.0467 a.u.), all the basis sets apart from cc-pVDZ and cc-pVTZ achieve sub-benchmark accuracy. The cc-pV5Z and cc-pV6Z basis set achieve errors that are one order of magnitude smaller than the above target error and the cc-pV{Q,5}Z extrapolation reproduces the cc-pV{5,6}Z re exactly.
It is also of interest to examine the basis set convergence of the vibrational transition frequencies (v = 1–5) obtained from the FCI/cc-pVnZ potential energy curves (n = D, T, Q, 5, and 6). These results are presented in Table 1. For all the basis sets considered, the errors with respect to the FCI/cc-pV{5,6}Z vibrational transition frequencies increase in the order Δv1 < Δv2 < Δv3 < Δv4 < Δv5. The largest errors (obtained for v5) are −399.1 (cc-pVDZ), −74.7 (cc-pVTZ), −23.4 (cc-pVQZ), −9.6 (cc-pV5Z), and −5.5 (cc-pV6Z) cm−1. Table S2 in the Supplementary Material lists the relative errors in the vibrational transition frequencies. Inspection of these results reveals that the relative errors are fairly constant across all the vibrational transition frequencies (v1–v5). Namely, they are ~81 % (cc-pVDZ), ~12 % (cc-pVTZ), ~3 % (cc-pVQZ), ~1.5 % (cc-pV5Z), and ~1.0 % (cc-pV6Z) cm−1. Overall, the results presented in Fig. 1 and Table 1 demonstrate that the FCI PES converges smoothly, albeit slowly, with the basis set size. The cc-pV{T,Q}Z and cc-pV{Q,5}Z basis set extrapolations provide significantly better performance than the cc-pVQZ and cc-pV5Z basis sets, respectively, at the same computational cost. The FCI/cc-pV{T,Q}Z PES provides a good compromise between accuracy and computational cost and results in errors in the BDE and vibrational transition frequencies that are smaller than or equal to ~10 cm−1.
Truncated Coupled-Cluster Methods
It is of interest to examine the performance of truncated CC theory in reproducing the entire PES for the beryllium dimer. Fig. 2 compares the HF, CCSD, CCSD(T), CCSDT, CCSDT(Q), and FCI PESs. Errors in the bond distance, BDE, and vibrational transition frequencies with respect to the FCI/cc-pV{5,6}Z values, as well as squared correlation coefficients (R2) with the FCI/cc-pV{5,6}Z PES are given in Table 2. In all cases, the energies are extrapolated to the complete basis set limit from the cc-pV5Z and cc-pV6Z basis sets. As expected,[14] the Hartree–Fock PES is purely repulsive over the entire PES. However, we note in passing that adding the original D3 dispersion correction[58] to the HF/cc-pV{5,6}Z energies results in a minimum of 312 cm−1 at 7.2 a.u. (Fig. S1 in the Supplementary Material). Replacing the zero-damping function in the original D3 procedure with the finite Becke–Johnson damping function leads to a more attractive PES, with a minimum of 2055 cm−1 at 5.1 a.u. (see Supplementary Material).[60] The valence CCSD/cc-pV{5,6}Z PES is strongly repulsive in the bonding region;[66] however, it exhibits a shallow minimum of 60.4 cm−1 at approximately 8.3 a.u. This is consistent with previous results obtained with smaller basis sets (see for example refs [8] and [14]). The CCSD(T)/cc-pV{5,6}Z level of theory reproduces the correct shape of the PES. The predicted bond distance is longer by 0.039 a.u. relative to the FCI/cc-pV{5,6}Z result; however, the PES is much too narrow and the binding energy is underestimated by as much as 219.5 cm−1. Consideration of higher-order connected triple excitations in the CCSDT/cc-pV{5,6}Z PES leads to an improvement; however, there is still a noticeable difference between the CCSDT and FCI PESs (with R2 = 0.9932) and the binding energy is still underestimated by 82.4 cm−1. The non-iterative connected quadruple excitations have a significant effect on the PES and the CCSDT(Q)/cc-pV{5,6}Z PES reproduces the FCI/cc-pV{5,6}Z curve almost perfectly (R2 = 0.9998), except in the vicinity of the equilibrium distance where there is still a visible difference between the curves (Fig. 2). In particular, the binding energy is underestimated by 16.6 cm−1.
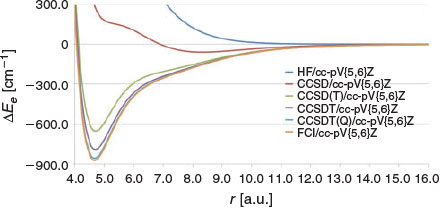
|
For all the truncated CC methods, the errors with respect to the FCI/cc-pV{5,6}Z vibrational transition frequencies increase in the order Δv1 < Δv2 < Δv3 < Δv4 < Δv5. Thus, it is informative to look at the largest errors obtained for v5: they are −459.5 (HF/CBS), −426.3 (CCSD/CBS), −92.4 (CCSD(T)/CBS), −35.6 (CCSDT/CBS), and −6.8 (CCSDT(Q)/CBS) cm−1. However, the relative errors in the vibrational transition frequencies (given in Table S3 in the Supplementary Material) are fairly constant across all the vibrational transition frequencies (v1–v5). Namely, they are ~98 % (HF/CBS), ~89 % (CCSD/CBS), ~14 % (CCSD(T)/CBS), ~6 % (CCSDT/CBS), and ~1 % (CCSDT(Q)/CBS) cm−1. Thus, it is evident, both from the perspective of the absolute errors and the relative errors, that CCSDT(Q) is the only method that achieves benchmark accuracy. We note, however, that the equilibrium distance has already converged to within 1 % with the CCSD(T) and CCSDT methods (namely, these methods attain errors of 0.039 and 0.027 a.u., respectively).
Density Functional Theory and Møller–Plesset Perturbation Theory
Fig. 3 shows the PESs of a few GGA functionals (Table S4 in the Supplementary Material lists errors in re, De, and vn). All the GGA functionals result in a PES that is much too wide and severely overbind the beryllium dimer. In particular, BLYP and PBE result in BDEs of 2163.0 and 3449.2 cm−1, respectively. revPBE results in a PES that is almost identical to that of PBE. As expected, addition of dispersion corrections increases the binding energies further and results in significantly larger BDEs (Fig. 3). In the remainder of this subsection, we will not consider dispersion corrections for DFT functionals that overbind the beryllium dimer. We have also considered the local non-separable gradient approximation N12 functional, which results in a BDE sandwiched between those of the BLYP and PBE functionals. Interestingly, both the BLYP and N12 functionals exhibit a shallow maximum at long distances. For BLYP, the height of this maximum is 47.5 cm−1 around re = 9.6 a.u. and for N12 it is 136.7 cm−1 around re = 8.9 a.u.
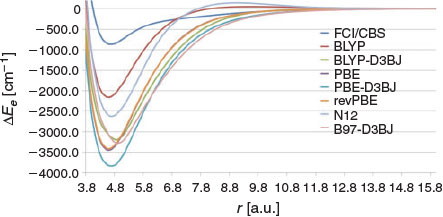
|
Despite the fact that the GGA functionals in Fig. 3 give a very poor description of the FCI/cc-pV{5,6}Z PES, their errors in the equilibrium bond distances are not very large. In particular, BLYP and PBE underestimate re by ~0.08 a.u. and N12 overestimates it by ~0.03 a.u.
Hybrid GGA functionals are expected to perform better than GGAs because the purely repulsive Hartree–Fock potential compensates for the severe overbinding of the GGAs. Fig. 4 gives the PESs for several HGGAs. Inspection of this figure reveals that HGGAs with low percentages of HF exchange still severely overbind the Be2 dimer, albeit to a lesser extent than the GGAs. The popular B3LYP functional (20 % HF exchange) predicts a binding energy of 1492.1 cm−1. This represents a significant improvement over BLYP, which predicts a BDE of 2163.0 cm−1. Replacing the LYP correlation functionals with PW91 results in a significantly wider PES and a binding energy of 2085.9 cm−1. In contrast, BH&HLYP with 50 % exact exchange severely underbinds the dimer, with a binding energy of 374.8 cm−1. Inclusion of the D3BJ dispersion correction overcorrects for this deficiency and leads to a binding energy of 1288.2 cm−1. The PBE0 functional (25 % HF exchange) results in a very wide PES and a binding energy of 2307.7 cm−1. This represents a significant improvement over PBE, which predicts a binding energy of 3449.2 cm−1.
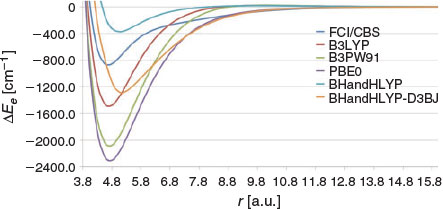
|
Fig. 5 depicts the PESs obtained with several hybrid-meta GGA from the Truhlar group. It is instructive to compare the PESs obtained with M06 (27 % exact exchange), M06–2X (54 % exact exchange), and M06-HF (100 % exact exchange). M06 severally overbinds the Be2 dimer and predicts a binding energy of 1822.8 cm−1. M06-HF underbinds the dimer with a binding energy of 760.7 cm−1. However, M06-2X predicts a binding energy of 928.8 cm−1, which deviates from the FCI values by only 55.9 cm−1. In terms of predicting the binding energy, M06-2X shows the best performance of all the conventional DFT functionals (i.e. excluding the DHDFT methods). Nevertheless, it should be pointed out that M06-2X does not give a good representation of the shape of the FCI PES as demonstrated, for example, from a squared correlation coefficient of R2 = 0.8783 with the FCI/cc-pV{5,6}Z PES.
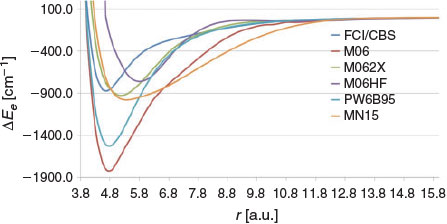
|
Nearly all of the GGA, HGGA, and HMGGA functionals considered so far tend to overbind the Be2 dimer (the only exceptions being BH&HLYP and M06-HF). In contrast, the considered range-separated functionals tend to systematically underbind the dimer. These results are presented in Fig. 6. LC-BLYP gives a very shallow PES with a minimum of 95.8 cm−1 at ~7 a.u. LC-PBE better represents the FCI PES, but still shows poor performance with a wide PES and a binding energy of 677.5 cm−1. These results should be compared with the results for BLYP and PBE, which severely overbind the Be2 dimer (Fig. 3). Similarly, CAM-B3LYP results in a BDE of 418.8 cm−1, in contrast to B3LYP, which predicts a binding energy of 1492.1 cm−1 (Fig. 4). Finally, we note that wB97X-D gives the best performance, with a BDE of 735.9 cm−1, which is lower than the FCI BDE by 137.0 cm−1.
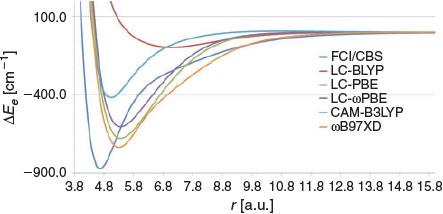
|
Fig. 7 gives the PESs obtained with several double-hybrid DFT functionals. With the exception of three functionals (PBE0-DH, B2GP-PLYP, and DSD-BLYP), all the DHDFT functionals considered show surprisingly good performance in both reproducing the shape and binding energy of the FCI/CBS PES. Let us begin with the poor performers. Both DSD-BLYP and B2GP-PLYP underbind the Be2 dimer; for example, B2GP-PLYP underbinds it by 201.9 cm−1 with a BDE of 670.9 cm−1. Addition of the D3BJ dispersion correction overcorrects for this deficiency and results in a very wide PES and a BDE of 1207.4 cm−1. PBE0-DH gives an even wider PES with a binding energy of 1626.3 cm−1. All of the other DHDFT functionals reproduce the FCI/CBS PES very well. The older-generation B2-PLYP and mPW2-PLYP predict binding energies that are too low by 46.7 and 40.3 cm−1, respectively. It is also worth pointing out that mPW2-PLYP predicts the FCI/CBS vibrational transition frequencies to within 10 cm−1 (Table 3). Quite remarkably, the more recently developed spin-component-scaled DHDFT DSD-PBEP86 functional reproduces the FCI/CBS PES spot on with a binding energy of 872.3 cm−1, less than 1 cm−1 from the FCI/CBS binding energy.
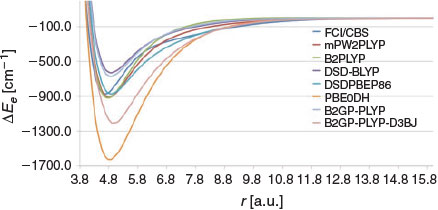
|
Finally, it is of interest to compare the performance of DHDFT with MPn theory. These results are presented in Fig. 8. Inspection of Fig. 8 reveals that the MPn series up to MP4 converges monotonically towards the FCI solution in the order MP2 → MP2.5 → MP3 → MP3.5 → MP4. For example, the following binding energies are obtained: 440.3 (MP2), 524.4 (MP2.5), 614.4 (MP3), 693.5 (MP3.5), and 783.3 (MP4) cm−1. However, the MP4.5 and MP5 PESs provide no further improvement and are practically identical to the MP4 PES (e.g. the predict binding energies of 786.2 (MP4.5) and 790.7 (MP5) cm−1). In light of these results, it is clear that DHDFT provides a much better description of the PES compared with the MPn methods.
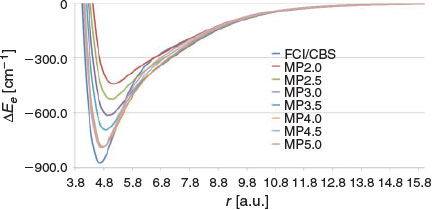
|
Conclusions
We have obtained the entire PES of the beryllium dimer at the FCI/cc-pV{5,6}Z level of theory. We use this reference data to evaluate (i) the basis set convergence of the valence FCI method; (ii) the performance of truncated CC methods at the infinite basis-set limit; (iii) the performance of DFT methods across the rungs of Jacob’s Ladder; and (iv) the performance of standard and modified MPn methods. Our main findings can be summarized as follows:
-
The FCI/cc-pV{T,Q}Z basis set extrapolation reproduces the shape of the FCI/cc-pV{5,6}Z PES as well as the binding energy and vibrational transition frequencies to within ~10 cm−1.
-
Of the truncated CC methods, CCSDT(Q)/cc-pV{5,6}Z provides a very good representation of the FCI/cc-pV{5,6}Z PES.
-
GGA functionals, as well as hybrid-GGA and hybrid-meta-GGA functionals with low percentages of exact exchange tend to severely overbind the Be2 dimer over the entire PES.
-
Range-separated functionals tend to underbind the Be2 dimer.
-
DHDFT functionals show exceptionally good performance relative to their computational cost.
-
Møller–Plesset perturbation theory converges smoothly up to fourth order; however, fifth-order corrections have a minor effect on the PES.
Supplementary Material
Absolute energies at all the considered levels of theory (Table S1); relative errors in the vibrational transition frequencies for the ab initio methods (Tables S2 and S3); errors in the bond distance, BDE, and vibrational transition frequencies for the DFT and MPn methods with respect to the FCI/cc-pV{5,6}Z values, as well as squared correlation coefficients (R2) with the FCI/cc-pV{5,6}Z PES (Table S4); and PES calculated at the HF-D3/cc-pV{5,6}Z and HF-D3BJ/cc-pV{5,6}Z levels of theory (Fig. S1) are available on the Journal’s website.
Conflicts of Interest
The authors declare no conflicts of interest.
Acknowledgements
This research was undertaken with the assistance of resources from the National Computational Infrastructure (NCI), which is supported by the Australian Government. We also acknowledge system administration support provided by the Faculty of Science at the University of Western Australia to the Linux cluster of the Karton group. A. K. gratefully acknowledges an Australian Research Council (ARC) Future Fellowship (FT170100373).
References
[1] A. Kalemos, J. Chem. Phys. 2016, 145, 214302.| Crossref | GoogleScholarGoogle Scholar |
[2] M. Lesiuk, M. Przybytek, M. Musial, B. Jeziorski, R. Moszynski, Phys. Rev. A 2015, 91, 012510.
| Crossref | GoogleScholarGoogle Scholar |
[3] S. Sharma, T. Yanai, G. H. Booth, C. J. Umrigar, G. K.-L. Chan, J. Chem. Phys. 2014, 140, 104112.
| Crossref | GoogleScholarGoogle Scholar |
[4] V. V. Meshkov, A. V. Stolyarov, M. C. Heaven, C. Haugen, R. J. LeRoy, J. Chem. Phys. 2014, 140, 064315.
| Crossref | GoogleScholarGoogle Scholar |
[5] M. El Khatib, G. L. Bendazzoli, S. Evangelisti, W. Helal, T. Leininger, L. Tenti, C. Angeli, J. Phys. Chem. A 2014, 118, 6664.
| Crossref | GoogleScholarGoogle Scholar |
[6] J. Koput, Phys. Chem. Chem. Phys. 2011, 13, 20311.
| Crossref | GoogleScholarGoogle Scholar |
[7] J. M. Merritt, V. E. Bondybey, M. C. Heaven, Science 2009, 324, 1548.
| Crossref | GoogleScholarGoogle Scholar |
[8] K. Patkowski, R. Podeszwa, K. Szalewicz, J. Phys. Chem. A 2007, 111, 12822.
| Crossref | GoogleScholarGoogle Scholar |
[9] J. M. L. Martin, Chem. Phys. Lett. 1999, 303, 399.
| Crossref | GoogleScholarGoogle Scholar |
[10] L. Fusti-Molnar, P. G. Szalay, J. Phys. Chem. 1996, 100, 6288.
| Crossref | GoogleScholarGoogle Scholar |
[11] S. Evangelisti, G. L. Bendazzoli, L. Gagliardi, Chem. Phys. 1994, 185, 47.
| Crossref | GoogleScholarGoogle Scholar |
[12] G. A. Petersson, W. A. Shirley, Chem. Phys. Lett. 1991, 181, 588.
| Crossref | GoogleScholarGoogle Scholar |
[13] R. J. Bartlett, J. D. Watts, S. A. Kucharski, J. Noga, Chem. Phys. Lett. 1990, 165, 513.
| Crossref | GoogleScholarGoogle Scholar |
[14] G. A. Petersson, W. A. Shirley, Chem. Phys. Lett. 1989, 160, 494.
| Crossref | GoogleScholarGoogle Scholar |
[15] V. E. Bondybey, Chem. Phys. Lett. 1984, 109, 436.
| Crossref | GoogleScholarGoogle Scholar |
[16] A. Karton, WIREs Comput. Mol. Sci. 2016, 6, 292.
| Crossref | GoogleScholarGoogle Scholar |
[17] N. Sylvetsky, K. A. Peterson, A. Karton, J. M. L. Martin, J. Chem. Phys. 2016, 144, 214101.
| Crossref | GoogleScholarGoogle Scholar |
[18] K. A. Peterson, D. Feller, D. A. Dixon, Theor. Chem. Acc. 2012, 131, 1079.
| Crossref | GoogleScholarGoogle Scholar |
[19] A. Karton, S. Daon, J. M. L. Martin, Chem. Phys. Lett. 2011, 510, 165.
| Crossref | GoogleScholarGoogle Scholar |
[20] A. Karton, P. R. Taylor, J. M. L. Martin, J. Chem. Phys. 2007, 127, 064104.
| Crossref | GoogleScholarGoogle Scholar |
[21] N. Mardirossian, M. Head-Gordon, Mol. Phys. 2017, 115, 2315.
| Crossref | GoogleScholarGoogle Scholar |
[22] L. Goerigk, A. Hansen, C. A. Bauer, S. Ehrlich, A. Najibi, S. Grimme, Phys. Chem. Chem. Phys. 2017, 19, 32184.
| Crossref | GoogleScholarGoogle Scholar |
[23] L. Goerigk, S. Grimme, Phys. Chem. Chem. Phys. 2011, 13, 6670.
| Crossref | GoogleScholarGoogle Scholar |
[24] R. Peverati, D. G. Truhlar, Phil. Trans. R. Soc. A 2014, 372, 20120476.
| Crossref | GoogleScholarGoogle Scholar |
[25] A. Karton, J. M. L. Martin, J. Chem. Phys. 2010, 133, 144102.
| Crossref | GoogleScholarGoogle Scholar |
[26] MRCC, a quantum chemical program suite written by M. Kállay et al. See also: http://www.mrcc.hu (verified 13 July 2018).
[27] Z. Rolik, L. Szegedy, I. Ladjanszki, B. Ladoczki, M. Kállay, J. Chem. Phys. 2013, 139, 094105.
| Crossref | GoogleScholarGoogle Scholar |
[28] T. H. Dunning, J. Chem. Phys. 1989, 90, 1007.
| Crossref | GoogleScholarGoogle Scholar |
[29] R. A. Kendall, T. H. Dunning, R. J. Harrison, J. Chem. Phys. 1992, 96, 6796.
| Crossref | GoogleScholarGoogle Scholar |
[30] T. H. Dunning, K. A. Peterson, A. K. Wilson, J. Chem. Phys. 2001, 114, 9244.
| Crossref | GoogleScholarGoogle Scholar |
[31] C. Lee, W. Yang, R. G. Parr, Phys. Rev. B 1988, 37, 785.
| Crossref | GoogleScholarGoogle Scholar |
[32] A. D. Becke, Phys. Rev. A 1988, 38, 3098.
| Crossref | GoogleScholarGoogle Scholar |
[33] J. P. Perdew, K. Burke, M. Ernzerhof, Phys. Rev. Lett. 1996, 77, 3865.
| Crossref | GoogleScholarGoogle Scholar |
[34] J. P. Perdew, K. Burke, M. Ernzerhof, Phys. Rev. Lett. 1997, 78, 1396.
| Crossref | GoogleScholarGoogle Scholar |
[35] M. Ernzerhof, J. P. Perdew, J. Chem. Phys. 1998, 109, 3313.
| Crossref | GoogleScholarGoogle Scholar |
[36] S. Grimme, S. Ehrlich, L. Goerigk, J. Comput. Chem. 2011, 32, 1456.
| Crossref | GoogleScholarGoogle Scholar |
[37] R. Peverati, D. G. Truhlar, J. Chem. Theory Comput. 2012, 8, 2310.
| Crossref | GoogleScholarGoogle Scholar |
[38] A. D. Becke, J. Chem. Phys. 1993, 98, 5648.
| Crossref | GoogleScholarGoogle Scholar |
[39] P. J. Stephens, F. J. Devlin, C. F. Chabalowski, M. J. Frisch, J. Phys. Chem. 1994, 98, 11623.
| Crossref | GoogleScholarGoogle Scholar |
[40] J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh, C. Fiolhais, Phys. Rev. B 1992, 46, 6671.
| Crossref | GoogleScholarGoogle Scholar |
[41] C. Adamo, V. J. Barone, Chem. Phys. 1999, 110, 6158.
[42] A. D. Becke, J. Chem. Phys. 1993, 98, 1372.
| Crossref | GoogleScholarGoogle Scholar |
[43] Y. Zhao, D. G. Truhlar, Theor. Chem. Acc. 2008, 120, 215.
| Crossref | GoogleScholarGoogle Scholar |
[44] Y. Zhao, D. G. Truhlar, Acc. Chem. Res. 2008, 41, 157.
| Crossref | GoogleScholarGoogle Scholar |
[45] Y. Zhao, D. G. Truhlar, J. Phys. Chem. A 2006, 110, 13126.
| Crossref | GoogleScholarGoogle Scholar |
[46] Y. Zhao, D. G. Truhlar, J. Phys. Chem. A 2005, 109, 5656.
| Crossref | GoogleScholarGoogle Scholar |
[47] H. S. Yu, X. He, S. L. Li, D. G. Truhlar, Chem. Sci. 2016, 7, 5032.
| Crossref | GoogleScholarGoogle Scholar |
[48] H. Iikura, T. Tsuneda, T. Yanai, K. Hirao, J. Chem. Phys. 2001, 115, 3540.
| Crossref | GoogleScholarGoogle Scholar |
[49] T. Yanai, D. Tew, N. Handy, Chem. Phys. Lett. 2004, 393, 51.
| Crossref | GoogleScholarGoogle Scholar |
[50] J.-D. Chai, M. Head-Gordon, Phys. Chem. Chem. Phys. 2008, 10, 6615.
| Crossref | GoogleScholarGoogle Scholar |
[51] L. Goerigk, S. Grimme, WIREs Comput. Mol. Sci. 2014, 4, 576.
| Crossref | GoogleScholarGoogle Scholar |
[52] S. Grimme, J. Chem. Phys. 2006, 124, 034108.
| Crossref | GoogleScholarGoogle Scholar |
[53] T. Schwabe, S. Grimme, Phys. Chem. Chem. Phys. 2006, 8, 4398.
| Crossref | GoogleScholarGoogle Scholar |
[54] A. Karton, A. Tarnopolsky, J.-F. Lamère, G. C. Schatz, J. M. L. Martin, J. Phys. Chem. A 2008, 112, 12868.
| Crossref | GoogleScholarGoogle Scholar |
[55] S. Kozuch, D. Gruzman, J. M. L. Martin, J. Phys. Chem. C 2010, 114, 20801.
| Crossref | GoogleScholarGoogle Scholar |
[56] S. Kozuch, J. M. L. Martin, Phys. Chem. Chem. Phys. 2011, 13, 20104.
| Crossref | GoogleScholarGoogle Scholar |
[57] É. Brémond, C. Adamo, J. Chem. Phys. 2011, 135, 024106.
| Crossref | GoogleScholarGoogle Scholar |
[58] S. Grimme, J. Antony, S. Ehrlich, H. Krieg, J. Chem. Phys. 2010, 132, 154104.
| Crossref | GoogleScholarGoogle Scholar |
[59] S. Grimme, WIREs Comput. Mol. Sci. 2011, 1, 211.
| Crossref | GoogleScholarGoogle Scholar |
[60] A. D. Becke, E. R. Johnson, J. Chem. Phys. 2005, 123, 154101.
| Crossref | GoogleScholarGoogle Scholar |
[61] M. Pitonak, P. Neogrady, J. Cerny, S. Grimme, P. Hobza, ChemPhysChem 2009, 10, 282.
| Crossref | GoogleScholarGoogle Scholar |
[62] A. Karton, L. Goerigk, J. Comput. Chem. 2015, 36, 622.
| Crossref | GoogleScholarGoogle Scholar |
[63] M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, D. J. Fox, Gaussian 16, Revision A.03 2016 (Gaussian, Inc.: Wallingford, CT).
[64] S. N. Yurchenko, L. Lodi, J. Tennyson, A. V. Stolyarov, Comput. Phys. Commun. 2016, 202, 262.
| Crossref | GoogleScholarGoogle Scholar |
[65] J. Tennyson, L. Lodi, L. K. McKemmish, S. N. Yurchenko, J. Phys. B 2016, 49, 102001.
| Crossref | GoogleScholarGoogle Scholar |
[66] A. Karton, J. M. L. Martin, J. Phys. Chem. A 2007, 111, 5936.
| Crossref | GoogleScholarGoogle Scholar |
* Amir Karton was awarded the 2018 Le Fèvre Medal from the Australian Academy of Science.





