Evaluating a seasonal, sex-specific size-structured stock assessment model for the American lobster, Homarus americanus

We would like to thank Atlantic States Marine Fisheries Commission (ASMFC) Lobster Model Development Subcommittee, Technical Committee and Stock Assessment Subcommittee for their support in the model development and testing. Comments from Dr L. Jacobson, Dr P. Breen, K. McKnown, J. Idoine, R. Glenn, Dr J. Wilson, Dr L. Mercer, Dr V. Crecco, P. Howell and S. Correia greatly improved the model. In particular, we are indebted to Dr L. Jacobson for his help and encouragement. We also would like to thank the ASMFC Lobster Model Peer Review Committee chaired by Dr R. Hilborn for their constructive comments, which greatly improved the early version of the model. Two anonymous referees and Dr A. Boulton are thanked for their useful comments on an earlier draft of this manuscript. Financial support of the work is provided by the Maine Sea Grant, Maine Department of Maine Resources, and ASMFC.

Atlantic States Marine Fisheries Commission (ASMFC) (2000). American Lobster Stock Assessment Report. ASMFC American Lobster Stock Assessment, Washington D.C. Available at http://www.asmfc.org/speciesDocuments/lobster/annualreports/stockassmtreports/lobsteradvisoryreport00.pdf (Accessed on November 1, 2007)

Atlantic States Marine Fisheries Commission (ASMFC) (2004). American Lobster Stock Assessment Model Technical Review, Terms of Reference and Panel Report, ASMFC Special Report No. 82, Washington D.C.

Atlantic States Marine Fisheries Commission (ASMFC) (2006). Terms of Reference and Advisory Report to the American Lobster Stock Assessment Peer Review. ASMFC Report 06–03, Washington D.C. Available at http://www.asmfc.org/speciesDocuments/lobster/annualreports/stockassmtreports/lobsterAdvisoryReport06.pdf (Accessed on 1 November 2007)

Breen, P. A. , Andrew, N. L. , and Kendrick, T. H. (2000). Stock assessment of PAU 5B for 1998–99. National Institute of Water and Atmospheric Research, Wellington, New Zealand.  ,
Chen Y., and Rajakaruna H. (2003). Impacts of quantity and quality of fisheries data on stock assessment. In ‘Proceedings of the 3rd World Fisheries Congress’. (American Fisheries Society: Bethesda, MD.)

Chen, Y. , Kanaiwa, M. , and Wilson, C. (2005). Developing and evaluating a Bayesian stock assessment framework for the American lobster fishery in the Gulf of Maine. New Zealand Journal of Freshwater and Marine Sciences 39, 645–660.
Cooper R. A., and Uzmann J. R. (1980). Ecology of juvenile and adult Homarus. In ‘The Biology and Management of Lobsters. Vol. 2’. (Eds J. S. Cobb and R. Phillips.) pp. 97–141. (Academic Press: New York.)

Fogarty, M. J. , and Idoine, J. S. (1988). Application of a yield and egg production model based on size to an offshore American lobster population. Transactions of the American Fisheries Society 117, 350–362.
| Crossref | GoogleScholarGoogle Scholar | Hilborn R., and Walters C. (1992). ‘Quantitative Fisheries Stock Assessment: Choice, Dynamics, and Uncertainty.’ (Chapman and Hall: New York.)

Kanaiwa, M. , Chen, Y. , and Hunter, M. (2005). Assessing stock assessment framework for the green sea urchin fishery in Maine, USA. Fisheries Research 74, 96–115.
| Crossref | GoogleScholarGoogle Scholar | Lawton P., and Lavalli K. L. (1995). Postlarval, juvenile, adolescent and adult ecology. In ‘Biology of the lobster Homarus americanus’. (Ed. J. F. Factor.) pp. 47–88. (Academic Press: New York.)

National Research Council (NRC) (1997). ‘Improving Fish Stock Assessments.’ (National Academy Press: Washington, D.C.)

Palma, A. T. , Steneck, R. S. , and Wilson, J. (1999). Settlement-driven, multiscale demographic patterns of large benthic decapods in the Gulf of Maine. Journal of Experimental Marine Biology and Ecology 241, 107–136.
| Crossref | GoogleScholarGoogle Scholar | Quinn T., and Deriso R. B. (1999). ‘Quantitative Fish Dynamics.’ (Oxford University Press: Oxford.)

Sheehy, M. R. J. (2001). Implications of protracted recruitment for perception of the spawner-recruit relationship. Canadian Journal of Fisheries and Aquatic Sciences 58, 641–644.
| Crossref | GoogleScholarGoogle Scholar | Wilson C. J. (1998). Bathymetric and spatial patterns of settlement in American lobsters, H. americanus, in the Gulf of Maine: Insights into processes controlling abundance. Masters Thesis. University of Maine, Orono, ME.

Because of large variations among individuals, recruitment in a given year can come from up to seven year classes (Sheehy 2001). Previous studies suggested a weak stock-recruitment relationship. To avoid the potential problem, no functional relationship was assumed between spawning stock biomass (SSB) and subsequent recruitment in the present study. If we assume an average recruitment for all the years considered in the assessment is R, the recruitment of a given year can be calculated as:

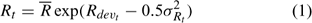
where R_t is the recruitment for year t, R_devt is the recruitment deviation from R for year t and can be calculated as:

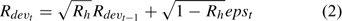
and σ_Rt is the standard deviation of the estimated recruitment for all the years included in the assessment and eps_t describes the part of the variation in R_t with the other part described by R_{devt – 1} of the previous year (Chen et al. 2005). Parameter R_h is an autocorrelation coefficient describing the degree of autocorrelations of recruitment of one year with the recruitment of the previous year. Its values range from 0 to 1, respectively, indicating no autocorrelation and perfect autocorrelation of the recruitment in years t and t – 1 (Breen et al. 2000). Recruitment only occurs in summer and fall, corresponding to major and minor molting events respectively. The minor molting occurs to a defined proportion of small individuals that have their second molt after the major molt.

Thirty-five size classes are defined, starting from 53 mm carapace length (CL) with a width of 5 mm. The choice of 5 mm for size class width is determined by the fact that the lobsters in most size classes have minimum molting increment of equal or larger than 5 mm (ASMFC 2000).

The lobster fishery started in 1800, but reliable information is not available from the early stages of the fishery. Thus we cannot treat the lobster as a virgin population for modelling. We need to estimate parameters that describe the size composition of the lobster stock in the first year defined in the assessment ( pⁱ_k,1) and initial population size (Nⁱ₁), where i and k index sex and size class, respectively. The number of lobsters in size class k in the beginning of the first assessment season can be calculated as:

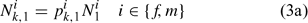
Initially, we directly estimated pⁱ_k,1 (35 size classes for each sex, equivalent to 70 parameters to be estimated) and Nⁱ₁ (one parameter for each sex, equivalent to two parameters to be estimated; Chen et al. 2005). The ASMFC Lobster Model Peer Review Committee suggests using a log-normal density distribution function to describe pⁱ_k,1. Thus, we have:

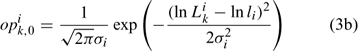
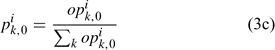
Equation (3c) is used to standardise the value of opⁱ_k,1 calculated from the log-normal function in Eqn (3b) to ensure that the summation of pⁱ_k,1 over all size classes is 1. This reduces the number of parameters to be estimated for pⁱ_k,1 from 70 (Chen et al. 2005) to 4 (i.e. l_i and σ_i for females and males). Thus, six parameters need to be estimated for defining Nⁱ_k,1 in Eqn (3a).

There is no evidence for sex-specific natural mortality before the first size class. Thus we assume a sex ratio of recruitment to the model of 0.5. The recruitment is equally divided among the first three size classes, considering the maximum increment in a molt can reach 16 mm. Thus, we have:

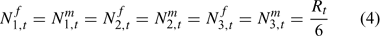
The pre-season total biomass, B_t^{total, i}, and pre-season legal biomass, B_t^{legal, i}, in year t for sex i can be estimated as:

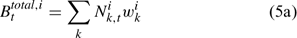
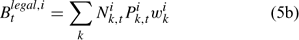
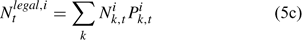
where wⁱ_k is the weight of the lobster in size k, and P_k,t is a switch (0 for size classes below the minimum legal size or above the maximum legal size, and 1 for legal size classes). The exploitation rate, Uⁱ_t, can then be calculated as:

where LCⁱ_t is the landings in year t observed in the fishery measured in biomass (6a) or in number (6b). U in Eqns (6a) and (6b) is the biomass-based exploitation rate (Eqn 6a) and number-based exploitation rate (Eqn 6b).

No size impact is considered in calculating the overall exploitation rate using Eqn 6. The following approach was used for estimating the size-specific exploitation rate Uⁱ_k,t. Considering various size-specific selectivity processes, the overall selectivity for lobsters of size k in time t, Sⁱ_k,t, can be estimated as:

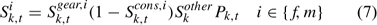
where S_k,t^gear,i is the gear selectivity coefficient describing the proportion of lobster in size k, time t encountering and then retained in traps, S_k,t^cons,i is the selectivity resulting from conservation measures such as V-notching and protection of egg-bearing lobsters, and describes the proportion of the lobsters in size k, sex i, and time t caught in traps, but thrown back to waters due to the conservation measures. S_k^other is the selectivity resulting from reasons other than gear selectivity, conservation measures and legal sizes for lobsters in size k to the fishery (Chen et al. 2005). The values of S_k,t^gear,i and S_k,t^cons,i are provided as input data (ASMFC 2000). The S_k^other is assumed to be invariant between sexes and over time, and follows a normal distribution function N(μ_S, σ_S²). The values of the normal distribution function are standardised to range from 0 to 1. The μ_S and σ_S² determine the shape and location of the S_k^other and are parameters to be estimated in modelling. Because the overall selectivity Sⁱ_k,t is the product of four selectivity coefficients and the legal switch has values of 0 and 1, the impacts of S_k,t^gear,i, S_k,t^cons,i and S_k^other on overall selectivity Sⁱ_k,t are limited to lobsters of legal sizes (Sⁱ_k,t is 0 for all other size classes because of P_k,t). The exploitation rate for lobsters of sex i in size class k in year t, Uⁱ_k,t, can be calculated as:

where Uⁱ_t is calculated from Eqn 6 (Chen et al. 2005). The exploitation rate derived in Eqn 8 is biomass-based if Uⁱ_t in Eqn (6a) is used, and is abundance-based (i.e. number-based) if Eqn (6b) is used.

The survival rate from fishing, SVⁱ_k,t, can then be calculated as:

The number of lobsters in size class k in year t, Nⁱ_k,t, is calculated as:

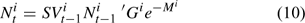
where G is the size-specific growth transition matrix and M is the instantaneous rate of natural mortality. Natural mortality was assumed to consist of two components: natural mortality due to molting (M₂) and average natural mortality resulting from all other natural causes (M₁). Different natural mortality rates were assumed for different seasons to account for the seasonal difference in the lobster life-history process. The natural mortality rate for winter and spring was assumed to be M₁. Because molting mainly occur in summer, natural mortality in summer was assumed to be M₁ + M₂. A proportion of lobsters that molt in summer also tend to molt in fall (ASMFC 2000). Thus the natural mortality for fall was assumed to be M₁ + αM₂, where α has a value between 0 and 1 for reflecting that only small proportion of lobsters tend to have second molt in a given year.

Because of the complexity of the framework, the growth transition matrix is determined outside the framework based on size-specific molting frequency and molting increment defined by the ASMFC Lobster Stock Assessment Subcommittee using an individual-based Lobster Simulator described in ASMFC (2006). Equation 10 is used in projecting the lobster population dynamics.

Using the above population dynamics models we can simulate a model lobster fishery. The following predictions can be made from the simulated model fishery.

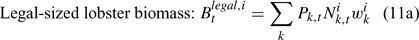
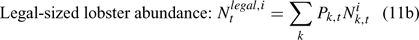
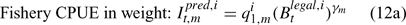
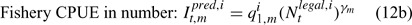
where m indexes season, fishery catchability qⁱ_1,m is calculated as biomass-based:

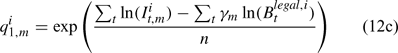
or abundance-based:

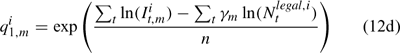
where γ in Eqn 12 is a density-dependent parameter, and Eqns (12) implicitly assume that catchability differs among seasons and between sexes in the fishery and survey.

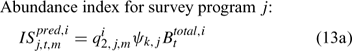
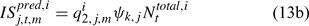
where Eqns (13a) and (13b) correspond to biomass and abundance-based survey indices, respectively, j ∈ {NMFS survey, DMR inshore survey and MA inshore survey in the present study} and survey’s catchability qⁱ_2,j,m can be calculated as:

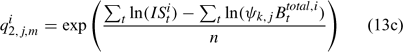
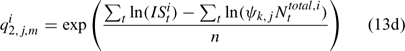
and ψ_k,j in Eqn 13 is the proportion of lobsters in size class k that is covered by survey program j, and can be described by the following logistic curve:

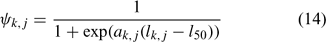
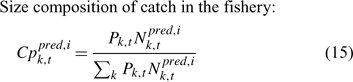
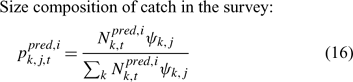
In the simulation and application, we used the number (abundance)-based data in the parameter estimation.

A group of observational models are developed to relate the predictions from the above dynamics models with the observations made in the fishery. The differences between the predicted and observed output variables in the observational models are assumed to be random and follow certain statistical distributions, which are then used to formulate the likelihood functions needed in the Bayesian parameter estimation. The following observational models are developed:

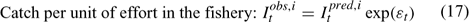
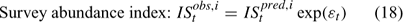
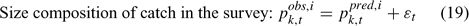
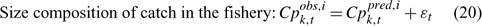
Error terms ϵ in Eqns 17 and 18 are assumed to follow normal distributions, and error terms ϵ in Eqns 19 and 20 are assumed to have multinomial distributions (Fournier et al. 1990).

Three different likelihood functions used in Chen et al. (2000) are considered: (a) normal; (b) robust normal; and (c) t-distribution functions. The following likelihood functions are formulated based on the observational models listed above:

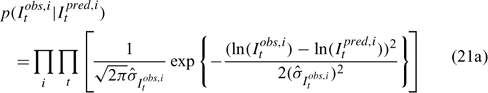
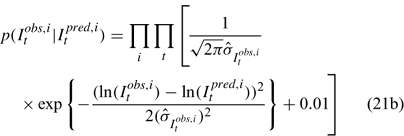
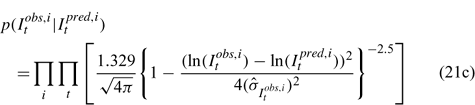
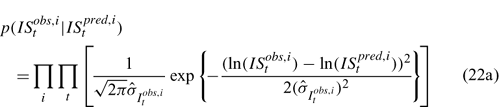
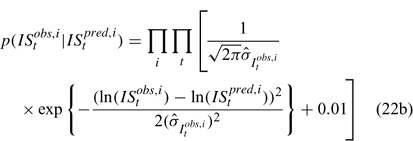
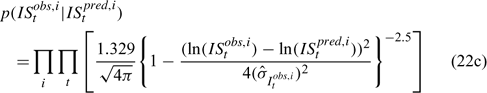
For the size composition data, a robust function (Fournier et al. 1990; Fournier 1996; Chen and Fournier 1999; Chen et al. 2000) described below is used,