Sea level trajectories and recent records at Australian tide gauges
Ben S. Hague A * , David A. Jones B , Jason West
A * , David A. Jones B , Jason West  C and Dörte Jakob A
C and Dörte Jakob A
A
B
C
Handling Editor: Anthony Rea
Abstract
Australian mean sea levels are rising faster than in the past. We find that sea level is accelerating by 0.113 ± 0.065 mm year−2, based on national tide gauge-based composite mean sea level anomalies from 1966 to 2022. Half of all Australian tide gauges recorded their highest-on-record annual mean sea levels in either 2021 or 2022 and 77% of all current monthly mean sea level records were set since 2010. Record flood levels were set 2.4 times more frequently since 2010 than would be expected without sea level rise and variability. Assuming recent accelerations persist, established methods can be used to estimate that Australian mean sea level will be 0.26 ± 0.03 m above 1995–2014 levels for 2050. This trajectory suggests that higher sea-level rise scenarios represent pathways more consistent with the observed sea-level rise trajectory over the past 50 years.
Keywords: acceleration, Australia, coastal adaptation, coastal flooding, mean sea level, sea level extremes, sea-level rise, tide gauges.
1Introduction
Sea-level variability and trends on annual-to-decadal timescales modulate spatiotemporal patterns of Australian coastal flood hazards (Hague et al. 2022). Mean sea level (MSL) has been rising faster in recent years (Watson 2020; Hague et al. 2022), amplifying the flood hazard. Day-to-day sea level extremes are substantially driven by tides and storm surges (Haigh et al. 2014a; McInnes et al. 2016). Sea-level rise (SLR) and interannual sea level variability, such as due to the El Niño–Southern Oscillation (ENSO) are generally most prominent when considering monthly and annual timescales (White et al. 2014; Lowe et al. 2021; Viola et al. 2024; O’Grady et al. 2025). The Interdecadal Pacific Oscillation (IPO) influences MSL in Australia over longer time periods (Zhang and Church 2012). Distinguishing between sea level variability due to the IPO and sea level rise due to thermal expansion and ice melt resulting from climate change typically requires half-century-long timeseries, at least in historical data (White et al. 2014).
Previous studies for other climate variables, like temperature (e.g. Barriopedro et al. 2011), have assessed observed changes in the frequency of records of annual and monthly means of the variable. We perform the first such analysis for Australian sea levels, quantifying the recency of current record annual maximum hourly and annual (average) MSL records being set. Previous SLR studies (Church and White 2006; Nerem et al. 2018; Wang et al. 2021; Hamlington et al. 2022) have used quadratic extrapolations of regional and global annual MSL to estimate future SLR and compare these to climate model-based projections. We perform the first such Australian-specific analysis using Australia’s reference tide gauge dataset. This paper also serves as a brief update to recent estimates of trends in mean and extreme sea levels (Hague et al. 2022), with a focus on record-setting.
2Data and methods
2.1 Data
We obtained tide gauge data from the Australian National Collection of Homogenised Observations of Relative Sea Level (ANCHORS, Hague et al. 2021). Routine updates of ANCHORS have appended new quality-controlled data to the existing homogenised timeseries. Periods of lower confidence were removed from the tide gauge timeseries as these are not suitable for trend or extremes analysis (Hague et al. 2021). ANCHORS was chosen as it is homogenised, with raw data corrected for non-geophysical artefacts in the data, such as those induced by equipment upgrades and site moves.
Future MSL is obtained from the global MSL projection from the 6th Assessment Report (AR6) of the Intergovernmental Panel on Climate Change (IPCC) (Fox-Kemper et al. 2021) to compare to observation-based trajectories. Vertical land motion in Australia is generally small compared to other regions globally, or if present, occurs at local scales due to local processes (Burgette et al. 2013; Rezvani, Watson and King 2022). Further, increases in MSL around Australia are expected to closely follow changes in the global mean (Zhang et al. 2017). This justifies the use of global MSL for comparative purposes in this study.
2.2 Site-based mean and record sea levels
Annual and monthly MSLs were computed as the average of all hourly observations in each calendar year or month at each site with the requirement of 70% completeness. This completeness criterion follows previous studies (Hague et al. 2022), and balances the need to have enough data for the annual mean to be representative of the experienced conditions but for the completeness requirement to not be so onerous that years that are largely complete are discarded. We performed a test of how sensitive our results are to different completeness criteria (Section 3.1). The highest hourly observations at each gauge are considered ‘record floods’ as these maxima exceed published impact-based thresholds for all assessed stations (Hague et al. 2022, 2023). We also estimated the theoretical rate of record setting without a changing climate or variability by assuming that the likelihood of setting a record is equal to the reciprocal of the timeseries length each year (Power and Delage 2019). For example, the probability of a record occurring in each year of a 20-year timeseries is 0.05 (i.e. 1/20). This simplified analysis requires no assumptions around base rates.
2.3 National composite mean sea levels, trends and extrapolation
A national composite MSL timeseries (anomaly relative to 1995–2014 mean) was produced following the process described in Hague et al. (2022) (see their section 3.1.1) for years 1966–2022. This maximal period was used as it is long enough for acceleration to be robustly detected (Haigh et al. 2014b) and to lessen possible contamination by the IPO signal (White et al. 2014).
It is well acknowledged that SLR is accelerating (e.g. Dangendorf et al. 2019; Frederikse et al. 2020; Hamlington et al. 2024), with numerous studies using quadratic or other non-linear representations for SLR contributions to observed changes in mean and extreme sea levels (e.g. Li et al. 2022; Thiéblemont et al. 2023; Treu et al. 2024). Quadratic trends can also be used to generate a future trajectory for SLR, based on these historical accelerations (Church and White 2006; Nerem et al. 2018; Wang et al. 2021; Hamlington et al. 2022). We show by comparison to other SLR representations (Section 3.1) that such an approach is justified for Australia. Regardless, we note (Section 4) that future extrapolations may be unreliable into the far future as conditions may deviate from their past trajectory.
The quadratic trend was estimated by fitting an ordinary least-squares model to the composite annual MSL anomaly timeseries using statsmodels (ver. 0.13.2, see https://www.statsmodels.org/stable/index.html; Seabold and Perktold 2010) in Python. The acceleration in sea level is computed as twice the quadratic coefficient (Church and White 2006; Wang et al. 2021). We consider the 5th, 50th and 95th percentile estimates of acceleration and extrapolate these out to 2100 by solving the differential equation of motion under uniform acceleration:
where t is the time in years after 2022 and α is the acceleration; st is the total increase in mean sea level relative to the 1995–2014 national averaged MSL at time t, for example, t = 3 corresponds to the estimate of national averaged MSL in 2025, above the 1995–2014 value, hence s0 is the amount of SLR for the year 2022 estimated from the regression of observed annual MSL; and u0 is the velocity at year 2022, estimated as the (first) difference of the 2022 and 2021 values of the quadratic regression of observed annual MSL. Based on our results in Section 3.1, we take s0 as 0.068 m, u0 as 0.00534 m year−1 and α as 0.000178 m year−2. These extrapolations are compared to global MSL projections from the IPCC AR6 (Fox-Kemper et al. 2021).
Although this approach is statistically robust, we are aware of criticisms of using high order trends in forecasting, which can result in unrealistic values (e.g. Lamberson and Firman 2002). Accordingly, we additionally construct a nonlinear trend from a sequence of linear segments using detrended fluctuation analysis (DFA). To obtain projections from the detrended analysis we use an extended exponential smoothing approach. This involves a linear forecast equation:
where and . Here, lt and bt are estimates of level and trend, α and β are smoothing parameters for level and trend at time t, whereas ϕh is a dampening parameter to moderate the trend and avoid over-forecasting over long time horizons. The initial values for lt, bt and ϕh are 0.037, 0.0036 and 0.0391 respectively, and the smoothing parameters α and β are 0.0054 and 0.0056 respectively. These values were calibrated for the Australian data based on a fit between year and SLR in metres above 1995–2014 mean.
3Results
3.1 Sea level trend
We compare the quadratic and piecewise linear trends to a Lowess smoothed timeseries generated using an implementation of Cleveland (1979) in statsmodels (Seabold and Perktold 2010) (Fig. 1). Since 1966, nationally averaged MSL has increased 0.124 m based on quadratic ordinary least-squares fitting, 0.127 m based on the Lowess smoothing and 0.117 m based on the piecewise linear regression. The piecewise approach identifies a single estimated break point occurring in 1993 with a distinct shift in slope. This slope estimates a SLR of 3.97 mm year−1 over the 1993–2022 period. Based on our quadratic fit, sea level accelerated at 0.113 mm year−2 (95% confidence interval: 0.048–0.178 mm year−2) over 1966–2022, indicating a statistically significant acceleration. This can be interpreted as SLR increasing by 1.13 mm year–1 more every decade. Our central estimate for acceleration sits above the upper limit of the confidence interval for global sea level acceleration over 1971–2018 (0.066–0.080 mm year−2) (Fox-Kemper et al. 2021). This higher acceleration could be due to the several record-breaking years since 2018 experienced in Australia (Section 3.2). The trend has led to the four highest national composite annual MSLs occurring after 2010 (Fig. 1a). There is strong coherence between each gauge, especially from the mid-1990s (Fig. 1b).
(a) Timeseries of national annual average mean sea level (MSL) for 1966–2022 (black), with Lowess smoothing (dashed), quadratic (dark red dash-dot) and piecewise linear (light blue dotted) trends, and (b) annual means for each site along with national annual average MSL.
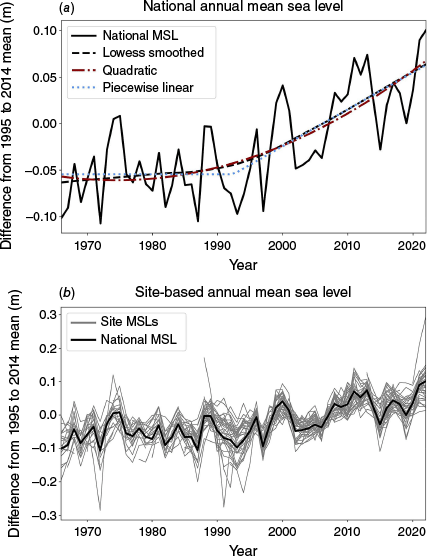
The increase in MSL since the IPCC baseline period helps decision makers understand how observations are tracking relative to projections and the associated planning benchmarks (Department of Energy Environment and Climate Action 2023). We estimate how much higher MSL is in 2022 compared to its mean value over the 1995–2014 baseline period used by the IPCC. Using the quadratic fit, MSL is 0.067 m higher than the 1995–2014 mean. Similar estimates of 0.064 and 0.063 m were found using Lowess smoothing and piecewise linear regression respectively. For example, this means that as of 2022, 0.067 m out of the 0.20 m being planned for by 2040 in Victoria has already occurred (Department of Energy Environment and Climate Action 2023).
Both quadratic and piecewise linear representations offer a better fit to the observations than a single linear trend over the 1966–present period as used in previous studies (White et al. 2014; Hague et al. 2022), providing strong statistical evidence to support a conclusion that SLR is accelerating. First, the piecewise linear regression indicates a significant acceleration. Second, the quadratic coefficient in the 1966–2022 quadratic model is significant (P = 0.005). Third, including the quadratic coefficient results in a better fit to the data and lower root mean square error (RMSE) of 0.0003 and R2 = 0.56 than if it is omitted (R2 = 0.49, RMSE = 0.013). Fourth, the Akaike and Bayes Information Criteria are lower if the quadratic coefficient is included than if it is omitted, suggesting that this fit is sufficiently better to justify the additional complexity compared to a linear alternative.
We also tested the sensitivity of the national composite MSL to the minimum completeness criterion applied to identify whether there are sufficient data to compute an annual mean. We find that MSL does not depend greatly on the completeness criterion with RMSE of 0.003 m or less for completeness criteria of 50–90%, compared to the 70% used here. Relaxing the criterion to 50% only allows 35 more site-years to be included (a 2% increase), whereas tightening to 90% completeness reduces the number of site-years by 117 (7%).
3.2 Sea level records
In a stationary climate (i.e. one with no trends and variability), we would expect the current record sea level to have an equal probability of having been set in any previous year when an annual maximum was recorded (Section 3.1; Power and Delage 2019). Based on this principle, the current site-based record annual MSLs were set disproportionately late in the observation period as 36 of 37 locations had their current annual MSL record set in 2010 or after (Fig. 2a), which is 3.5 times greater than would be expected under stationarity. Out of these 36 locations, half set their record annual MSL in either 2021 or 2022. Records set in the last 2 years of the data period were 8.7 and 14.7 times more frequent than would be expected in a stationary climate respectively.
The year when the current annual (a) average MSL record and (b) maximum hourly sea level record was set for Australian tide gauges.
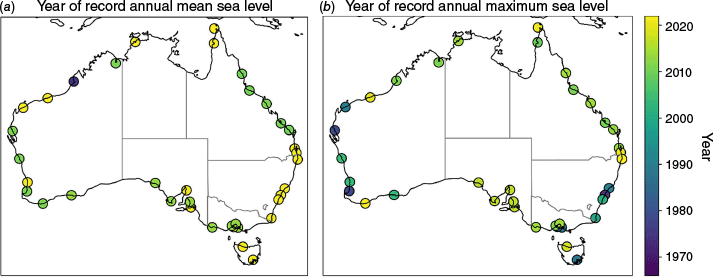
Current record flood levels (i.e. the highest of all hourly observations) were also set disproportionately late in the observation period, albeit less so than for the MSL records (Fig. 2b). The current record flood level was set at 24 locations from 2010 onwards, which is 2.4 times greater than the expected number of current records to have been over this period without a trend. The smaller increases in frequency of record maxima compared to record means is explained by signal-to-noise ratio arguments: the variability between years in annual MSLs is much less than the variability of annual maxima for Australian tide data. The mean standard deviation of annual mean and maximum sea levels across all tide gauges are 0.055 and 0.139 m respectively. As the climate change signal similarly affects mean and extreme sea level elevations in Australia (e.g. Colberg and McInnes 2012), the difference between signal-to-noise ratios for means and maxima is essentially a function of the difference in variability between each metric (i.e. the noise).
Monthly MSL records also occur more frequently in the latter part of the observational timeseries (Fig. 3). The number of current site-based monthly records found in the most recent decade is 7.8 times greater than the number in the first decade. Of all current monthly records, 77% were set during 2010–2022. This is 3.4 times greater than would be expected without a changing climate. This analysis has accounted for lower data density in the early part of the record by computing counts using the ratios of missing data in each year (World Meteorological Organisation 2017). For example, if 1966 only has 70% of the total expected station-months then all record counts are divided by 0.7. In aggregate these data show clearly that across hourly, monthly and annual timescales, record setting is now being strongly influenced by the rise in MSL.
The number of current monthly MSL records set in calendar year across all sites in the ANCHORS dataset each year (adjusted for missing data). The shading within the bars shows the breakdown of how records are distributed by calendar month. Austral winter months are shown as darker colours and austral summer months are shown as lighter colours. La Niña year marked with an asterisk (black for single year, red for multi-year), based on classifications by Huang et al. (2024).
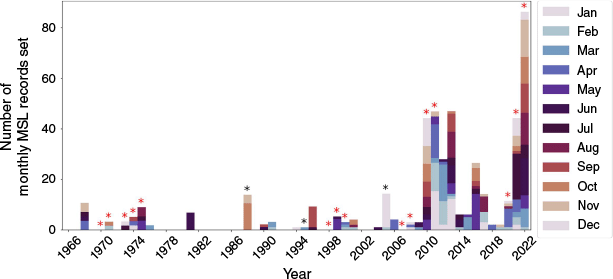
The years where the most site-based monthly MSL records were set coincide with multi-year episodes of the La Niña phase of ENSO (Huang et al. 2024). For example, 70 and 83% of locations set at least one monthly MSL record in 2021 and 2022 respectively. Similarly, 42 and 51% of locations set at least one monthly MSL record in 2010 and 2011 respectively. Whereas La Niña increases mean and extreme sea levels at many locations around Australia (Lowe et al. 2021; Viola et al. 2024), the fact that only recent La Niña events have been associated with large numbers of record sea levels (Fig. 3) highlights the accumulating impact of the trend. The recent La Niña may affect estimates of trends, although similarities between the trends computed here and those without the recent record years from earlier studies (White et al. 2014; Hague et al. 2022) suggest that this is not a first-order effect.
3.3 Future mean sea level trajectory
Noting the clear acceleration in Australian MSL, we explore here what a statistical extrapolation tells us about possible Australian sea level changes over coming decades. Extrapolating the observed quadratic trend of 0.113 mm year−2 [90% confidence interval: 0.048–0.178 mm year−2] estimates 2050 MSL as 0.26 ± 0.03 m [90% confidence interval] above 1995–2014 MSL, with further estimates of 0.45 ± 0.07 m for 2070 and 0.83 ± 0.20 m for 2100 (Fig. 4). The linear extrapolation, based on the exponential smoothing on the DFA, predicts 0.15 m SLR [0.09–0.25] by 2050 using an undampened parameter and 0.19 m SLR [0.13–0.27] using a damped parameter. High SLR scenarios (e.g. SSP5–8.5) published by the IPCC are most consistent with a continuation of the SLR trajectory that has been observed in the last 50 years (Fig. 4d), based on differences between the extrapolations and projections. For future MSL to be consistent with median estimate of low scenarios (e.g. SSP1–2.6) the observed acceleration must immediately cease, which seems unlikely given recent global temperatures (Fig. 4a).
Comparison of quadratic (dark red lines: median solid, dotted 5 and 95% estimates), linear with damped exponential smoothing (light blue lines: median solid, dotted 5 and 95% estimates) and IPCC AR6 global mean sea level (MSL) projections (median estimate black dashed line, shading representing 66 and 90% range). Four different emission scenarios are presented for the IPCC AR6 projections: (a) SSP1–2.6, (b) SSP2–4.5, (c) SSP3–7.0 and (d) SSP5–8.5. Observed nationally averaged annual MSL timeseries provided for reference (black solid line). Median estimates provided in Bureau of Meteorology (2024).

4Discussion and conclusions
In contrast to previous studies (e.g. Watson 2011, 2020) we detected significant accelerations in sea level around Australia. This is likely due to having several years more data and using a composite annual MSL timeseries rather than individual gauges, which increase the signal-to-noise ratio of SLR to interannual variability. The development of a national average MSL timeseries allows decision makers to easily see how Australian MSL is tracking relative to planning benchmarks and adaptation signals, triggers and thresholds, which are typically a set increment of SLR (Dedekorkut-Howes et al. 2021).
The SLR is now sufficient to be strongly influencing record sea levels occurring across hourly, monthly and annual timescales. The 2022 record annual MSL was 0.10 m above the 1995–2014 baseline. This annual MSL is expected to be the mean state by 2028 based on our near-term extrapolation (Fig. 4). In other words, the effect of higher sea level variability in 2022 reflecting a multi-year La Niña event is equivalent to only 6 years of future SLR. It is therefore expected that a new nationally averaged annual MSL record will be set this decade, even if no further strong La Niña events occur. More generally, future annual MSL records may not be associated with phases of climate drivers that have been historically associated with higher-than-average MSLs due to the increased SLR signals expected with ongoing acceleration.
The future extrapolations are not meant to be a reliable estimate of future sea level, which will depend on many factors including future greenhouse gas emissions, large ice-sheet dynamics and interannual variability. For example, our trajectories (both quadratic and piecewise linear) explicitly assume acceleration remains constant (at a median 0.113 mm year−2 and zero respectively). Further, parametric extrapolations assume the errors are normally distributed and have constant variance, which is not the case here for either linear or quadratic fits based on Kolmolgrov–Smirnov tests. Hence, the statistical extrapolation beyond a decade or two carries much greater uncertainty. We have shown that if the acceleration of sea level detected over the last 50 years continues, Australia is expected to experience SLR consistent with higher emission scenarios like those projected under SSP5–8.5. This is despite global mean temperatures likely tracking 3°C by 2100 based on current emissions reductions policies, which is more consistent with the lower SSP2–4.5 scenario (Meinshausen et al. 2020; Rogelj et al. 2023). Our finding agrees with expert judgement surveys of SLR scientists that have concluded that the IPCC SLR projections are likely too low compared to the expected response of other climate variables under the same global warming levels (Bamber et al. 2019; Horton et al. 2020).
Our extrapolations remain a useful means of assessing sea level benchmarks which have been aggregated or simplified from complex physics-based guidance (Hirschfeld et al. 2023). For example, the most recent SLR guidance to support adaptation planning in Australia (McInnes et al. 2015) provided SLR allowances that were less than 0.83 m (our median estimate for 2100 based on quadratic extrapolation) for all locations under RCP2.6 and RCP4.5, and for all but two locations under RCP8.5. Our results suggest that resultant state planning benchmarks of 0.8 m by 2100 (Dedekorkut-Howes et al. 2021) are implicitly assuming that historical acceleration will not increase beyond what has been persistently observed globally over the last 50 years (Dangendorf et al. 2019).
Reappraisal of planning guidelines may be needed for Australian decision makers to consider the possibility of increased acceleration of sea level occurring this century. By 2100, SLR could be well above 0.80 m if the projected impacts of tipping points associated with 2°C of warming are realised (Armstrong McKay et al. 2022; van de Wal et al. 2022; Kopp et al. 2023). These could be further compounded by changes in sea level variability (Widlansky, Long and Schloesser 2020; Li et al. 2021; Calafat et al. 2022; Hague and Talke 2024), changes in ocean currents (Sweet et al. 2016; Dangendorf et al. 2023) and vertical land motion (Nicholls et al. 2021; Tay et al. 2022). The resultant ‘deep uncertainty,’ and SLR being expected to continue beyond 2100 (DeConto et al. 2021; Box et al. 2022), has led to many jurisdictions in Australia and around the world adopting ‘decision-making under deep uncertainty’ approaches (Lawrence et al. 2022; Haasnoot et al. 2024; Lempert et al. 2024). These identify short-term and long-term adaptation options and the triggers for these actions to be taken (Lawrence et al. 2022). Although longer-term adaptation options should continue to be informed by the precautionary principle, ‘lack of full certainty should not be used as a reason for postponing measures to prevent environmental or other degradation’ (Boxshall 2022, p. 3), trajectories have the potential to reduce uncertainty of the timing of triggers emerging within the common decadal-scale governance horizons.
Data availability
The ANCHORS dataset can be downloaded from the NCI Data Catalogue (Bureau of Meteorology 2024). Computed annual and monthly MSLs, annual maxima and future SLR trajectories, are provided at the same location in the ‘MMSL’ sub-directory.
Declaration of funding
B. Hague, D. Jakob and D. Jones’s contributions were funded by the Australian Climate Service.
Acknowledgements
We thank the IPCC projection authors for developing and making the sea‐level rise projections available, multiple funding agencies for supporting the development of the projections and the NASA Sea Level Change Team for developing and hosting the IPCC AR6 Sea Level Projection Tool. We thank Robert Fawcett, Ryan Holmes and Danielle Udy (Bureau of Meteorology) for providing constructive feedback on an earlier version of this manuscript.
References
Armstrong McKay DI, Staal A, Abrams JF, et al. (2022) Exceeding 1.5°C global warming could trigger multiple climate tipping points. Science 377(6611), 7950.
| Crossref | Google Scholar | PubMed |
Bamber JL, Oppenheimer M, Kopp RE, et al. (2019) Ice sheet contributions to future sea-level rise from structured expert judgment. Proceedings of the National Academy of Sciences 116(23), 11195-11200.
| Crossref | Google Scholar | PubMed |
Barriopedro D, Fischer EM, Luterbacher J, et al. (2011) The hot summer of 2010 : redrawing the temperature record map of Europe. Science 332(6026), 220-224.
| Crossref | Google Scholar | PubMed |
Box JE, Hubbard A, Bahr DB, et al. (2022) Greenland ice sheet climate disequilibrium and committed sea-level rise. Nature Climate Change 12(9), 808-813.
| Crossref | Google Scholar |
Boxshall A (2022) Perspectives on building climate resilience via marine and coastal management from the governance frontline in Victoria, Australia. Ocean and Coastal Management 228, 106291.
| Crossref | Google Scholar |
Bureau of Meteorology (2024) Australian National Collection of Homogenised Observations of Relative Sea Level (ANCHORS). (BOM: Melbourne, Vic., Australia) [Dataset, published 28 September 2021, revised 19 December 2024] 10.25914/6142dff37250b
Burgette RJ, Watson CS, Church JA, et al. (2013) Characterizing and minimizing the effects of noise in tide gauge time series: relative and geocentric sea level rise around Australia. Geophysical Journal International 194(2), 719-736.
| Crossref | Google Scholar |
Calafat FM, Wahl T, Tadesse MG, et al. (2022) Trends in Europe storm surge extremes match the rate of sea-level rise. Nature 603(7903), 841-845.
| Crossref | Google Scholar | PubMed |
Church JA, White NJ (2006) A 20th Century acceleration in global sea-level rise. Geophysical Research Letters 33, 94-97.
| Crossref | Google Scholar |
Cleveland WS (1979) Robust locally weighted regression and smoothing scatterplots. Journal of the American Statistical Association 74(368), 829.
| Crossref | Google Scholar |
Colberg F, McInnes KL (2012) The impact of future changes in weather patterns on extreme sea levels over southern Australia. Journal of Geophysical Research: Oceans 117(8), C08001.
| Crossref | Google Scholar |
Dangendorf S, Hay C, Calafat FM, et al. (2019) Persistent acceleration in global sea-level rise since the 1960s. Nature Climate Change 9(9), 705-710.
| Crossref | Google Scholar |
Dangendorf S, Hendricks N, Sun Q, et al. (2023) Acceleration of US Southeast and Gulf coast sea-level rise amplified by internal climate variability. Nature Communications 14(1), 1935.
| Crossref | Google Scholar | PubMed |
DeConto RM, Pollard D, Alley RB, et al. (2021) The Paris Climate Agreement and future sea-level rise from Antarctica. Nature 593(7857), 83-89.
| Crossref | Google Scholar | PubMed |
Dedekorkut-Howes A, Torabi E, Howes M (2021) Planning for a different kind of sea change: lessons from Australia for sea level rise and coastal flooding. Climate Policy 21(2), 152-170.
| Crossref | Google Scholar |
Department of Energy Environment and Climate Action (2023) Victoria’s Resilient Coast: Adapting for 2100+. Framework and guidelines: a strategic approach to coastal hazard risk management and adaptation. (The State of Victoria) Available at https://www.marineandcoasts.vic.gov.au/__data/assets/pdf_file/0022/662503/Victorias-Resilient-Coast-Guidelines-.pdf
Fox-Kemper B, Hewitt HT, Xiao C, et al. (2021) 9 – Ocean, Cryosphere and Sea Level Change. In ‘Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change’. pp. 1211–1362. (Cambridge University Press) 10.1017/9781009157896.011
Frederikse T, Landerer F, Caron L, et al. (2020) The causes of sea-level rise since 1900. Nature 584(7821), 393-397.
| Crossref | Google Scholar | PubMed |
Haasnoot M, Di Fant V, Kwakkel J, et al. (2024) Lessons from a decade of adaptive pathways studies for climate adaptation. Global Environmental Change 88, 102907.
| Crossref | Google Scholar |
Hague BS, Talke SA (2024) The influence of future changes in tidal range, storm surge, and mean sea level on the emergence of chronic flooding. Earth’s Future 12(2), e2023EF003993.
| Crossref | Google Scholar |
Hague BS, Jones DA, Trewin B, et al. (2021) ANCHORS: a multi-decadal tide gauge dataset to monitor Australian relative sea level changes. Geoscience Data Journal 9(2), 256-272.
| Crossref | Google Scholar |
Hague BS, Jones DA, Jakob D, et al. (2022) Australian coastal flooding trends and forcing factors. Earth’s Future 10(2), e2021EF002483.
| Crossref | Google Scholar |
Hague BS, McGregor S, Jones DA, et al. (2023) The global drivers of chronic coastal flood hazards under sea-level rise. Earth’s Future 11, e2023EF003784.
| Crossref | Google Scholar |
Haigh ID, Wijeratne EMS, MacPherson LR, et al. (2014a) Estimating present day extreme water level exceedance probabilities around the coastline of Australia: tides, extra-tropical storm surges and mean sea level. Climate Dynamics 42(1–2), 121-138.
| Crossref | Google Scholar |
Haigh ID, Wahl T, Rohling EJ, et al. (2014b) Timescales for detecting a significant acceleration in sea level rise. Nature Communications 5, 3635.
| Crossref | Google Scholar | PubMed |
Hamlington BD, Chambers DP, Frederikse T, et al. (2022) Observation-based trajectory of future sea level for the coastal United States tracks near high-end model projections. Communications Earth and Environment 3(1), 230.
| Crossref | Google Scholar |
Hamlington BD, Bellas-Manley A, Willis JK, et al. (2024) The rate of global sea level rise doubled during the past three decades. Communications Earth and Environment 5(1), 601.
| Crossref | Google Scholar |
Hirschfeld D, Behar D, Nicholls RJ, et al. (2023) Global survey shows planners use widely varying sea-level rise projections for coastal adaptation. Communications Earth and Environment 4, 102.
| Crossref | Google Scholar | PubMed |
Horton BP, Khan NS, Cahill N, et al. (2020) Estimating global mean sea-level rise and its uncertainties by 2100 and 2300 from an expert survey. npj Climate and Atmospheric Science 3(1), 18.
| Crossref | Google Scholar |
Huang AT, Gillett ZE, Taschetto AS (2024) Australian rainfall increases during multi-year La Niña. Geophysical Research Letters 51(9), e2023GL106939.
| Crossref | Google Scholar |
Kopp RE, Oppenheimer M, O’Reilly JL, et al. (2023) Communicating future sea-level rise uncertainty and ambiguity to assessment users. Nature Climate Change 13(7), 648-660.
| Crossref | Google Scholar |
Lamberson WR, Firman JD (2002) A comparison of quadratic versus segmented regression procedures for estimating nutrient requirements. Poultry Science 81(4), 481-484.
| Crossref | Google Scholar | PubMed |
Lawrence J, Mackey B, Chiew F, et al. (2022) 11 – Australasia. In ‘Climate Change 2022: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change’. pp. 1581–1688. (Cambridge University Press) 10.1017/9781009325844.013.
Lempert RJ, Lawrence J, Kopp RE, et al. (2024) The use of decision making under deep uncertainty in the IPCC. Frontiers in Climate 6, 1380054.
| Crossref | Google Scholar |
Li S, Wahl T, Talke SA, et al. (2021) Evolving tides aggravate nuisance flooding along the US coastline. Science Advances 7(10), eabe2412.
| Crossref | Google Scholar | PubMed |
Li S, Wahl T, Barroso A, et al. (2022) Contributions of different sea-level processes to high-tide flooding along the US coastline. Journal of Geophysical Research: Oceans 127(7), e2021JC018276.
| Crossref | Google Scholar |
Lowe RJ, Cuttler MVW, Hansen JE (2021) Climatic drivers of extreme sea level events along the coastline of Western Australia. Earth’s Future 9(4), e2020EF001620.
| Crossref | Google Scholar |
McInnes KL, Chruch J, Monselesan D, et al. (2015) Information for Australian impact and adaptation planning in response to sea-level rise. Australian Meteorological and Oceanographic Journal 65(1), 127-149.
| Crossref | Google Scholar |
McInnes KL, White CJ, Haigh ID, et al. (2016) Natural hazards in Australia: sea level and coastal extremes. Climatic Change 139(1), 69-83.
| Crossref | Google Scholar |
Meinshausen M, Nicholls ZRJ, Lewis J, et al. (2020) The shared socio-economic pathway (SSP) greenhouse gas concentrations and their extensions to 2500. Geoscientific Model Development 13(8), 3571-3605.
| Crossref | Google Scholar |
Nerem RS, Beckley BD, Fasullo JT, et al. (2018) Climate-change-driven accelerated sea-level rise detected in the altimeter era. Proceedings of the National Academy of Sciences 115(9), 2022-2025.
| Crossref | Google Scholar | PubMed |
Nicholls RJ, Lincke D, Hinkel J, et al. (2021) A global analysis of subsidence, relative sea-level change and coastal flood exposure. Nature Climate Change 11(4), 338-342.
| Crossref | Google Scholar |
O’Grady JG, Stephenson A, McInnes K (2025) Drivers and predictability of extreme still water level trends and interannual variability along the coast of Australia across different time scales. Coastal Engineering 199, 104725.
| Crossref | Google Scholar |
Power SB, Delage FPD (2019) Setting and smashing extreme temperature records over the coming century. Nature Climate Change 9(7), 529-534.
| Crossref | Google Scholar |
Rezvani MH, Watson CS, King MA (2022) Vertical deformation and residual altimeter systematic errors around continental Australia inferred from a Kalman-based approach. Journal of Geodesy 96(12), 96.
| Crossref | Google Scholar |
Rogelj J, Fransen T, den Elzen M, et al. (2023) Credibility gap in net-zero climate targets leaves world at high risk. Science 380(6649), 1014-1016.
| Crossref | Google Scholar | PubMed |
Seabold S, and Perktold J (2010) Statsmodels: econometric and statistical modeling with Python. In ‘Proceedings of the 9th Python in Science Conference’, 28 June–3 July 2010, Austin, TX, USA. pp. 92–96. (Scipy Proceedings) 10.25080/majora-92bf1922-011.
Sweet WV, Menendez M, Genz A, et al. (2016) In tide’s way: southeast Florida’s September 2015 sunny-day flood. Bulletin of the American Meteorological Society 97, S25-S30.
| Crossref | Google Scholar |
Tay C, Lindsey EO, Chin ST, et al. (2022) Sea-level rise from land subsidence in major coastal cities. Nature Sustainability 5, 1049-1057.
| Crossref | Google Scholar |
Thiéblemont R, Le Cozannet G, D’Anna M, et al. (2023) Chronic flooding events due to sea-level rise in French Guiana. Scientific Reports 13(1), 21695.
| Crossref | Google Scholar | PubMed |
Treu S, Muis S, Dangendorf S, et al. (2024) Reconstruction of hourly coastal water levels and counterfactuals without sea level rise for impact attribution. Earth System Science Data 16(2), 1121-1136.
| Crossref | Google Scholar |
van de Wal RSW, Nicholls RJ, Behar D, et al. (2022) A high-end estimate of sea level rise for practitioners. Earth’s Future 10(11), e2022EF002751.
| Crossref | Google Scholar | PubMed |
Viola CNA, Verdon-Kidd DC, Power HE (2024) Spatially varying impacts of pacific and southern ocean climate modes on tidal residuals in New South Wales, Australia. Estuarine, Coastal and Shelf Science 305, 108869.
| Crossref | Google Scholar |
Wang J, Church JA, Zhang X, et al. (2021) Reconciling global mean and regional sea level change in projections and observations. Nature Communications 12(1), 990.
| Crossref | Google Scholar | PubMed |
Watson PJ (2011) Is there evidence yet of acceleration in mean sea level rise around Mainland Australia? Journal of Coastal Research 27(2), 368-377.
| Crossref | Google Scholar |
Watson PJ (2020) Updated mean sea-level analysis: Australia. Journal of Coastal Research 36(5), 915.
| Crossref | Google Scholar |
White NJ, Haigh ID, Chruch JA, et al. (2014) Australian sea levels – trends, regional variability and influencing factors. Earth-Science Reviews 136, 155-174.
| Crossref | Google Scholar |
Widlansky MJ, Long X, Schloesser F (2020) Increase in sea level variability with ocean warming associated with the nonlinear thermal expansion of seawater. Communications Earth and Environment 1, 9.
| Crossref | Google Scholar |
World Meteorological Organisation (2017) Guidelines on the calculation of climate normals. WMO-No. 1203. (WMO: Geneva, Switzerland) Available at https://library.wmo.int/idurl/4/55797
Zhang X, Church JA (2012) Sea level trends, interannual and decadal variability in the Pacific Ocean. Geophysical Research Letters 39(21), L21701.
| Crossref | Google Scholar |
Zhang X, Chruch JA, Monselesan D, et al. (2017) Sea level projections for the Australian region in the 21st Century. Geophysical Research Letters 44(16), 8481-8491.
| Crossref | Google Scholar |

