Variability of Australian climate and future changes
I. G. Watterson A *
A *
A
Abstract
The variability of climate is assessed using the observational fifth generation of the European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis (ERA5) for 1980–2019 and data from 35 Coupled Model Intercomparison Project Phase 6 (CMIP6) models for a suite of variables, including the vertically integrated horizontal moisture flux vector from 10 models. The standard deviation of the seasonal anomalies within the 40-year period is calculated for grid points and for rainfall averaged over Australian regions. The four-season average of standard deviation, denoted VAR, is a measure of overall variability. From ERA5, the average for grid points over Australia (AUS) is 4–11% higher than that from all land in 60°S–60°N (LAN) for each variable, except for flux and 850-hPa eastward wind, which are 31–41% higher. The variability linked to two mode indices, NINO34 and PID (Pacific–Indian Dipole), is quantified by the four-season average of the magnitude of the regression anomaly. For each index, the 35-model average (av35) of the linked variability averaged over AUS and LAN for rainfall, temperature and pressure is typically less than 30% of the net VAR. The statistics for 2040–2079 under the shared socioeconomic pathway with expected radiative forcing 5–8.5 W m−2 (SSP5-8.5) are scaled to provide a change representative of the 2°C global warming level. There is little change overall in VAR, except for moisture variables, with flux increasing typically 10%. From av35, for rainfall AUS increased 6% and LAN 9%, in part owing to an increase in the VAR of the NINO34 index of 14%. The PID index provides a stronger link to the range of model change of the variability of all-Australia rainfall, and hence the uncertainty in projected change.
Keywords: Australian climate, Australian rainfall, climate modes, climate variability, ENSO, ERA5, future climate, moisture flux, NINO34.
1.Introduction
It is commonly said (and written; see acknowledgements) that Australia has a highly variable climate, and that this variability is expected to increase with global warming. Typically, the focus of variability studies is the effect of the drivers or modes of variability El Niño–Southern Oscillation (ENSO), Indian Ocean Dipole (IOD) and Southern Annular Mode (SAM) on Australian rainfall and (surface air) temperature (e.g. Bureau of Meteorology and CSIRO 2022). However, even for seasonal means of these two quantities, how variability might change in the future is not clear (Lee et al. 2021), owing to the range of changes simulated by climate models. Among recent studies, Alexander et al. (2009) linked ENSO to observed extremes. Cai et al. (2023) analysed observed variability and trends in ENSO indices. McGregor et al. (2022) presented changes in anomalies linked to the sea surface temperature (SST) over the Niño3.4 region, and the mode index NINO34, in Coupled Model Intercomparison Project Phase 6 (CMIP6) models. Gu and Adler (2019) assessed precipitation, temperature and moisture transport anomalies linked to ENSO indices. Schubert et al. (2016) presented a synthesis of drought worldwide, including the role of SST drivers of variability. Holgate et al. (2020a, 2020b) considered the role of moisture transport in the development of droughts in Australia. Klingaman et al. (2013) focused on processes driving variation in Queensland rainfall. Chung et al. (2023) assessed the simulation of the links between modes and Australian rainfall by Coupled Model Intercomparison Project Phase 5 (CMIP5) and CMIP6 models. Watterson (2022, 2023) examined a suite of variables for present and future climates in 35 CMIP6 models, including the vertical integral of horizontal moisture transport, available from 10 models, and other quantities important to the atmospheric moisture budget and hence rainfall. Watterson (2020) and Watterson et al. (2021) examined seasonal anomalies in observational reanalysis data across an Indo-Pacific domain for NINO34, and a further SST index, Pacific–Indian Dipole (PID, defined shortly), which is well related to Australian rainfall. Maher et al. (2023) found that although the variability of ENSO indices increases in the future, in their average of multiple model ensembles, there is much variation across models and also across simulations from a single model. Furthermore, apparent biases in models in comparison with the pattern of observed SST trends add to the uncertainty in future change (e.g. Seager et al. 2022).
Compared to the many studies of modes of variability, relatively few studies have addressed the overall interannual variability of climate variables. Scherrer (2011) analysed the interannual standard deviation (s.d. here) of seasonal means in the ERA-Interim reanalysis and in CMIP3 models for temperature, precipitation and pressure in the present climate. Watterson et al. (2016) assessed the variability of monthly-mean rainfall over Australia, finding that extreme rainfall increased in CMIP5 models. Gutiérrez et al. (2021, table 1) showed the fractions of observed net seasonal variance of temperature and rainfall for regions over the globe that are linked to ENSO, SAM and other modes in the present climate. For Australian regions, this is typically no more than 25%, indicating that much variability is not linked to the standard indices. Power et al. (2013) found that simulated variability of rainfall over the equatorial Pacific increased considerably in a future warmer climate, with much of this variability linked to ENSO. Pendergrass et al. (2017) showed that the variability of precipitation tends to increase over much of the globe. Douville et al. (2021) presented similar results (e.g. their fig. 8.16) using CMIP6 models. Lee et al. (2021) showed (their fig. 4.21) that the simulated interannual s.d. of seasonal mean temperature tends to increase over land in the tropics and subtropics. Over northern land, it tends to increase in summer and decrease in winter.
Likewise, it seems that there have been few publications comparing the overall variability of climate variables over Australia with that elsewhere. Nicholls and Wong (1990) compared observed rainfall variability at locations around the globe and showed that the coefficient of variation (the s.d. divided by the mean rainfall) was relatively high over Australia. McMahon et al. (2007) extended such an assessment to hydrology and found that the variability of streamflow in Australian rivers is particularly high. However, Scherrer’s (2011, fig. 1) maps suggest that other places can be considerably more variable. It seems worthwhile to revisit this issue using the current fifth generation of the European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis (ERA5) and models.
The data sets used by Watterson (2023) are further analysed to consider the interannual variability of seasonal means of up to 12 variables, including moisture flux, starting with the present climate in the following section, where the variables and data are described. The skill of 10 CMIP6 models, compared with ERA5, in simulating the fields of s.d. of eight basic climate and moisture variables is assessed using the approach previously used for climatological means (Watterson 2023) but using an Indo-Pacific or IP domain. The overall variability, based on s.d.s from the four seasons, over Australia in these data sets is compared with that over global land. There is a further focus on rainfall averaged over ‘All Australia’ and six other Australian regions (including north, north of 26°S, and SWWA, south-west Western Australia), as used by the Bureau of Meteorology. The variability linked to the indices NINO34, representing ENSO, and PID, individually, in the data sets is assessed in Section 3. This variability is quantified using mode anomaly patterns based on regression, following Watterson (2020, 2022). In Section 4, these assessments are extended to the future climate simulated by the CMIP6 models, scaled to represent the global warming level of 2°C, following Watterson (2023). The spread of results for temperature and rainfall across the ensemble is examined in Section 5, and PID is again found to be well linked with All-Australia rainfall. Summaries are provided in each section, with the conclusions following in Section 6. Given the range of aspects, supporting results are presented in the Supplementary material, which comprises Supplementary Tables S1–S3 and Supplementary Fig. S1–S11. The domains and regions considered are plotted in Fig. S1.
2.Variability of seasonal means
2.1. Variables considered and quantification of variability
The full suite of variables in the data set acquired by Watterson (2023) includes the ‘basic climate variables’ surface air temperature or ‘tas’ (the CMIP6 short variable name), precipitation (pr) and mean sea level pressure (psl). In addition to pr are the other moisture quantities: evaporation from the surface, denoted here ‘evap’, the integrated water column (CMIP6 ‘prw’) and the vertically integrated horizontal moisture transport vector (eastward ‘intuaw’, northward ‘intvaw’). For convenience, this is termed ‘moisture flux’, with components (uq, vq). (In the data sets used here, these integrals are accurately calculated at the source, hence avoiding the need to approximate flux using winds, eastward u, northward v, and specific humidities q from time averages at standard levels; see Watterson 2023.) The convergence of the moisture flux, calculated using finite differences, is denoted ‘conv’. To provide a fuller depiction of circulation patterns, the vectors of wind at 850 hPa (or w850, components u850, v850) and 200 hPa are included. In addition, the fields of SST (CMIP6 ‘ts’) are used in constructing mode indices (see Section 3). Not all variables are used in each section.
All data were obtained as time series of monthly means, then averaged for the seasons December–February (DJF), March–May (MAM), June–August (JJA) and September–November (SON). The analysis focuses on Period 1 (or P1), 1980–2019 and Period 2 (P2), 2040–2079 (see Section 4). In forming the first DJF of each period, the December from the previous year is used. For the four seasons, each 40-year series is linearly detrended (to limit the effect of forced change), and the interannual s.d. is calculated. This is done for values from fields at individual grid points, rainfall averaged over Australian regions and the mode indices. Selected results for individual seasons are considered. As a quantification of ‘overall’ variability, the focusis on the four-season average of s.d., denoted ‘VAR’ (for variability, not variance). Climate mean results are denoted ‘CLIM’. Using the term AAUS to refer to the All-Australia spatial average, we can refer, for example, to the s.d. of AAUS pr (or rainfall) in SON and the VAR of AAUS pr. To distinguish VAR with a component of variability linked to a mode (Section 3), it can be denoted ‘net’ VAR. As with all climate statistics, values calculated from a period, even over 40 years, can differ from those from a longer period because of internal variability of the climate system.
2.2. Data sets
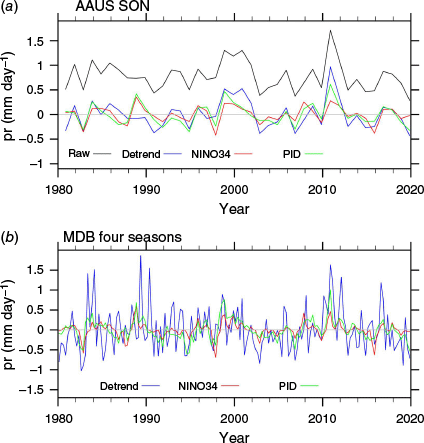
To represent the present climate (more accurately, the recent past), the ERA5 (Hersbach et al. 2020) from 1980 to 2019 is used. To illustrate the analysis, Fig. 1a shows the AAUS pr for SON. The detrended anomaly series features similar peaks, given little trend in this case. The s.d. is 0.30 mm day−1. The series of seasonal anomalies for Murray–Darling Basin (MDB, Fig. S1) rainfall, combining the four individual series, is shown in Fig. 1b, with peaks in various seasons. These examples have good links to the two mode indices shown, as will be discussed shortly. It is worth noting that for a variable with a normal distribution, the ratio of the mean magnitude of the anomalies to the distribution s.d. is as follows
Time series of regional average rainfall anomalies from ERA5 over 1980–2019: (a) All Australia in September–November (SON), with the raw series included (black); (b) Murray–Darling Basin (MDB) in all four seasons (see text). Shown are the detrended anomaly series (blue), and (detrended) regression anomaly series (Section 3.2) for indices NINO34 (red) and PID (green). For (a) (detrended) AAUS pr the s.d. is 0.30 mm day−1. The correlation r for NINO34 is −0.59 and for PID −0.75. For MDB, the overall variability VAR, from the four seasons, is 0.54 mm day−1 (Section 2.4.2).
For Fig. 1a (‘detrend’), the ratio is a little lower, at 0.78, consistent with the typical skewness of pr values, which would enhance the calculated s.d. Note that statistics given in the text are based on high-precision values.
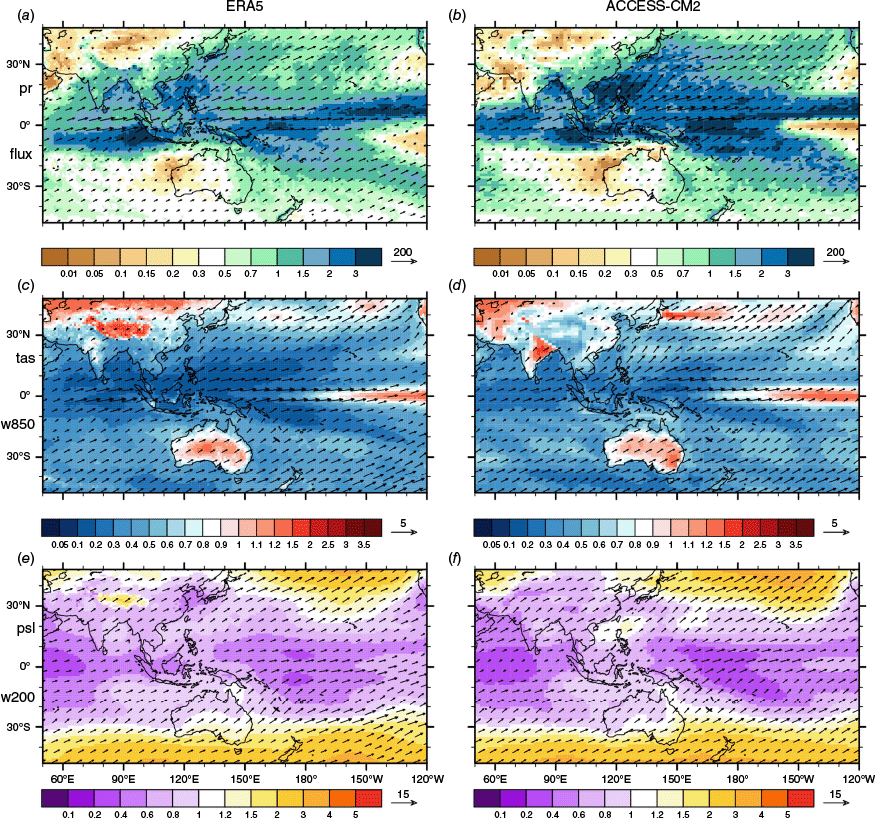
The s.d. fields for nine quantities in SON from ERA5 are plotted for the IP domain in Fig. 2 (left). The variability of pr (Fig. 2a, mm day−1) is high in much of the tropics. Eastern Australia has s.d. over 0.7 mm day−1 but east Asia has higher s.d. The mean of the s.d.s computed at each grid point over Australia is 0.47 mm day−1, 57% larger than the s.d. of the AAUS pr series (in Fig. 1a). This illustrates the usual result that s.d. is reduced by spatial averaging. The s.d. of the two moisture flux components (uq, vq) is shown as a vector, always pointing to the north-east quadrant, although the s.d. for eastward flux (uq) dominates to the north of New Guinea. The s.d. for temperature (tas, Fig. 2c) is typically higher over land, with the region used to define NINO34 (Fig. S1) prominent over ocean. The variability of pressure (psl, Fig. 2e) is low in the tropics and tends to increase poleward. The vectors for wind (u, v) at 200 hPa (Fig. 2e) match well those for 850 hPa (Fig. 2c) but with reference vector triple the magnitude. The s.d. fields for tas, pr and psl, from DJF and JJA (over this domain and globally, not shown) are similar to those for the earlier ERA-Interim reanalysis plotted by Scherrer (2011, fig. 1).
Variability of SON seasonal means from 1980 to 2019, quantified by the interannual standard deviation (s.d.) from ERA5 (left), and the model ACCESS-CM2 (right) over the IP domain. In this and all cases, the series are first linearly detrended. The shaded variables are: (a, b) pr (mm day−1); (c, d) tas (°C); and (e, f) psl (hPa). The vectors are (a, b) moisture flux (kg m−1 s−1); (c, d) wind at 850 hPa (m s−1); (e, f) wind at 200 hPa (m s−1), with reference vector length (for each vector component) shown. Vectors are shown at a spacing of not less than 0.4 times the reference vector length. The plots (a, c, e) use a 1.0° grid and (b, d, f) the model grid.
Using the data sets of Watterson (2023), time series of seasonal means for years 1980–2019 were calculated from the CMIP6 ‘historical’ simulations and their continuation under the shared socioeconomic pathway with expected radiative forcing 5–8.5 W m−2 (SSP5-8.5) scenario with strongly rising radiative forcing. The full suite of variables was analysed for the 10 models for which moisture flux is available (listed in Table 1). For an additional 25 models, tas, pr and psl were analysed. See Table S1 for the full list of models, the runs used and various statistics.
| Model | tas | pr | psl | Av-3 | uq | vq | conv | evap | prw | Av-6 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ACCESS-CM2 | 581 | 545 | 758 | 628 | 642 | 596 | 584 | 493 | 671 | 589 | |
| ACCESS-ESM1-5 | 540 | 496 | 765 | 601 | 549 | 561 | 526 | 462 | 582 | 529 | |
| CNRM-CM6-1-HR | 620 | 422 | 742 | 595 | 347 | 506 | 428 | 480 | 349 | 422 | |
| CNRM-CM6-1 | 626 | 579 | 753 | 653 | 503 | 607 | 572 | 475 | 617 | 559 | |
| CNRM-ESM2-1 | 632 | 535 | 745 | 637 | 455 | 573 | 527 | 458 | 583 | 522 | |
| HadGEM3-GC31-LL | 606 | 553 | 763 | 641 | 592 | 654 | 571 | 524 | 682 | 596 | |
| HadGEM3-GC31-MM | 638 | 562 | 804 | 668 | 643 | 625 | 586 | 552 | 685 | 609 | |
| IPSL-CM6A-LR | 526 | 489 | 694 | 570 | 411 | 538 | 513 | 473 | 578 | 500 | |
| MIROC-ES2L | 436 | 543 | 678 | 553 | 596 | 490 | 529 | 455 | 604 | 536 | |
| UKESM1-0-LL | 587 | 529 | 765 | 627 | 540 | 614 | 538 | 509 | 639 | 561 | |
| av10 | 684 | 659 | 831 | 725 | 630 | 708 | 652 | 621 | 722 | 665 | |
| av10 s.d. – CLIM | −236 | −80 | −40 | −119 | −217 | −90 | −79 | −176 | −163 | −134 | |
| r s.d. with pr s.d. | 0.09 | 1.00 | 0.26 | 0.55 | 0.73 | 0.63 | 0.93 | 0.32 | 0.88 | 0.88 | |
| r s.d. with CLIM | 0.60 | 0.38 | 0.75 | 0.86 | 0.50 | 0.67 | 0.53 | −0.08 | 0.82 | 0.48 | |
| r s.d. with NINO34 | 0.48 | 0.72 | 0.24 | 0.62 | 0.81 | 0.68 | 0.75 | 0.68 | 0.90 | 0.89 | |
| r s.d. with PID | 0.03 | 0.54 | 0.46 | 0.52 | 0.87 | 0.39 | 0.51 | 0.38 | 0.75 | 0.76 |
The values are the average of the four M scores in ‘points’ (maximum 1000) for the individual seasons, for each of eight quantities. The average M for tas, pr and psl ‘Av-3’ is a measure of the skill in basic variables. The average Av-6 for the six moisture-related quantities, pr, uq, vq, convergence of flux (conv), evaporation (evap) and prw, is given. Below, is firstly the av10 value (for s.d.) minus that for climatological means (CLIM); then the correlation coefficient, r, across the 10 model values, between the pr (s.d.) score with the scores in each column, between the s.d. and CLIM scores, and between s.d. and the scores for the regression anomaly fields for NINO34 and PID (see Section 3.3), all over IP. r values below the 0.1 significance level (0.55, for n = 10) are in italic. All values are non-dimensional.
As an example, Fig. 2 (right) shows s.d. fields for SON from the model ACCESS-CM2 (Schroeter et al. 2024). The pattern of variability in ERA5 over the IP domain and over Australia is well matched although, as is typical of CMIP6 models, the equatorial Pacific variability of tas tends to peak a little farther west, and in the western Pacific, the pr s.d. exceeds that in ERA5. The focus of later results is the multi-model mean of the 10-model ensemble, denoted av10 (as previously), and of the full ensemble, denoted av35. Both are calculated from data linearly interpolated to a common 1° grid.
2.3. Model skill in variability
Quantification of skill in variability is uncommon although Scherrer (2011) used the ratio of model and observational s.d. at grid points. Here, the focus is on the spatial pattern of variability, and the test previously used for means (CLIM) by Watterson (2023) is applied to the s.d. fields. To quantify the skill of a model field, in terms of its similarity to the corresponding ERA5 field, the arcsin-Mielke measure M is used:
with mse the mean square error, or bias, between model X and ERA5 Y, and V and G are the spatial variance and mean of the fields (as subscripted) over a domain. The measure is non-dimensional, and with the scaling in Eqn 1, a value of 1000 points holds for perfect agreement, whereas M of 0 or less means no skill. The average over the four seasons is used as a skill score for the variable. With the focus on variability and mode patterns over the broad Australian region, the IP domain is used. In the Fig. 2 case, the M scores for tas, pr and psl are 550, 559 and 771 respectively, indicating a moderately close match for each.
The average M over the four seasons is given in Table 1 for 8 variables from the 10 listed models. Most scores are between 500 and 700. As previously, the average M for tas, pr and psl is a score for skill in basic climate, denoted Av-3. The average score for the six moisture variables (see caption) is denoted Av-6. In both categories, the best score is for HadGEM3-GC31-MM. One likely reason it performs well (also in other tests) is its relatively high spatial resolution (see Watterson 2023). The bias of a model result, compared with ERA5, can be due to both its inaccuracy in representing the underlying (long-term) present climate and to the statistical uncertainty of a 40-year span. Such biases can be reduced through ensemble averaging. The scores for the av10 s.d. fields are, indeed, higher than for any model, except for the uq case. In all 10 cases, the av10 score for s.d. is not as high as that for CLIM, with the corresponding results calculated for the IP domain given in Table S2. The particularly high CLIM value for tas is consistent with its strong pole–equator gradient, which models simulate well because it is linked to solar radiation. As a further comparison, the correlation between the CLIM scores and the s.d. scores across the 10 models is given for each case. The coefficient r is high (0.86) for Av-3 and values are otherwise moderate, except for evaporation. These correlations, from a sample of 10, are statistically uncertain, but they suggest that models with better CLIM scores tend to give better s.d. scores. The original motivation for analysing the moisture flux and other budget terms was their link to precipitation. The correlations across the 10 models between the scores for pr and each other quantity are given in Table 1 (for s.d.) and in Table S2 (for CLIM). The s.d. value for conv is very high, owing to the close relationship between pr and conv, especially for changes (see Watterson 2023). In most other cases, the r values for the moisture terms are mostly moderate.
2.4. Overall variability (VAR) in P1
The four-season average of s.d., or VAR, fields from ERA5 is shown in Fig. 3, for most of the globe and with Australia in detail in the left panels. Variability of precipitation (Fig. 3a, b) tends to be larger where mean (CLIM) pr is large, including over Australia. Variability of moisture flux tends to follow that of pr, with the eastward flux component dominating near the equator. For tas (Fig. 3c, d), values over ice-free ocean tend to be relatively low, with the exception of the eastern equatorial Pacific. Values are particularly high over northern land, presumably enhanced by high s.d. of northward wind, as can be inferred from the overlying 850-hPa vectors. The variability of psl (Fig. 3e, f) is high over high-latitude ocean, peaking at 5 hPa over the far south-east Pacific.
As Fig. 2, but the overall variability of seasonal means, VAR (the four-season average of the interannual standard deviation), from ERA5. Vectors are spaced at no less than the reference length (or half that for the globe). The plots (a, c, e) for Australia use a 0.5° grid, and those for the globe (b, d, f), 1.5°.
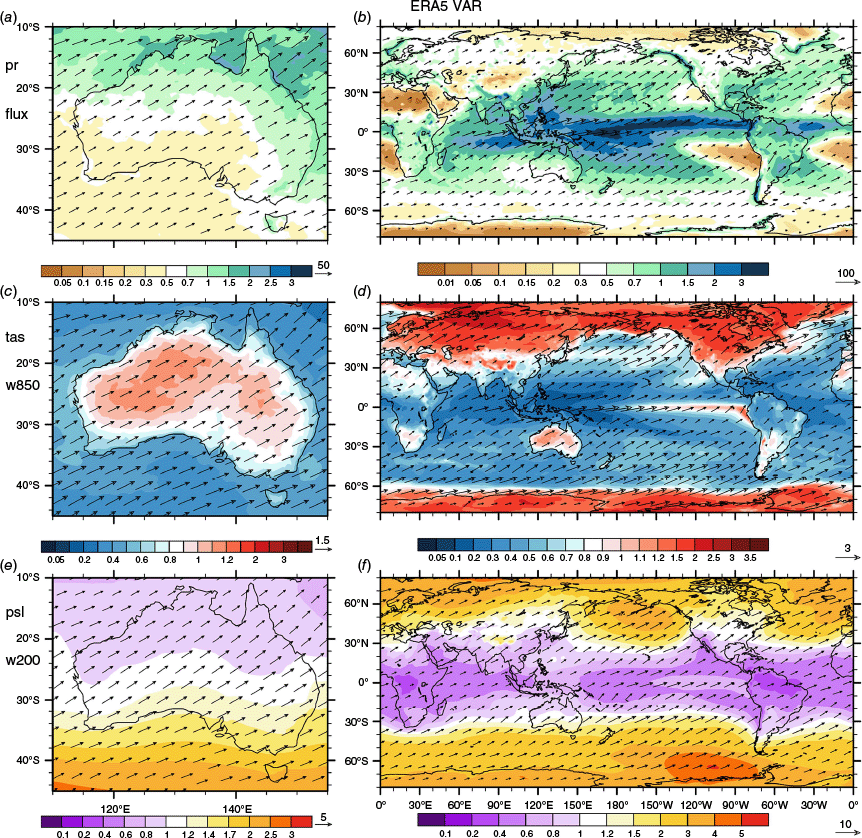
For a comparison of the overall variability of seasonal means, the spatial means of VAR for Australia and all land (including Australia) from 60°S to 60°N (LAN) are given in Table 2 for the nine variables in Fig. 3. The AUS values are higher (than LAN) for each variable but barely for tas (by 4%) and pr (7%), and somewhat higher for psl and the wind components (8–11%). For these six variables, there are areas of global land with considerably higher VAR than at points in Australia. Australia has notably higher variability of the moisture flux components (by 41, 31%) and of u850 (38%). The coefficient of variation for pr, pr-cv, is calculated as VAR divided by the four-season mean pr, at each grid point. This pr-cv is high over dry regions (not shown), reaching 1 in central Australia but over 2 in the Sahara and Arabian deserts. It is over 2 in the eastern equatorial Pacific also. The average over AUS is 54% higher than that for LAN. In summary, the interannual variability from ERA5 is on average only a little higher over Australia than over global land for basic climate variables but is notably higher for pr-cv and for moisture flux.
| Variable | ERA5 | av10 | Δ | Δ% | |||||
|---|---|---|---|---|---|---|---|---|---|
| LAN | AUS | LAN | AUS | LAN | AUS | LAN | AUS | ||
| tas | 0.869 | 0.904 | 0.937 | 0.906 | 0.003 | 0.022 | 0 | 2 | |
| pr | 0.676 | 0.720 | 0.736 | 0.786 | 0.056 | 0.015 | 8 | 2 | |
| pr-cv | 0.428 | 0.659 | 0.453 | 0.611 | 0.010 | 0.027 | 2 | 4 | |
| psl | 0.974 | 1.086 | 1.051 | 1.067 | −0.012 | −0.006 | −1 | −1 | |
| uq | 18.37 | 25.81 | 19.15 | 26.20 | 3.11 | 2.36 | 16 | 9 | |
| vq | 12.27 | 16.08 | 12.51 | 17.38 | 1.66 | 1.29 | 13 | 7 | |
| u850 | 0.769 | 1.062 | 0.906 | 1.121 | −0.014 | −0.050 | −2 | −4 | |
| v850 | 0.604 | 0.654 | 0.690 | 0.721 | −0.013 | −0.033 | −2 | −5 | |
| u200 | 2.974 | 3.210 | 3.096 | 3.380 | 0.079 | −0.026 | 3 | −1 | |
| v200 | 1.969 | 2.161 | 2.108 | 2.313 | −0.019 | −0.079 | −1 | −3 | |
The ERA5 is the observational reanalysis from 1980 to 2019 (P1), av10 is the average of 10 CMIP6 models (with flux data) for P1. The future change from these (Section 4), each scaled to 2°C GW (global warming), and denoted Δ, is given along with this change as a percentage of the av10 P1 spatial mean values. The quantities are surface air temperature (tas, °C), precipitation (pr, mm day−1) and the coefficient of variation (pr-cv, non-dimensional), mean sea level pressure (psl, hPa), then vectors moisture flux (uq, vq, kg m−1 s−1), wind at 850 hPa (u850, v850) and at 200 hPa (u200, v200) (m s−1). pr-cv is calculated at each grid point from the four-season VAR and the four-season climatological mean.
The four-season average VAR from av10, plotted for nine variables in Fig. S2, compares well with ERA5 (Fig. 3). The spatial averages for LAN and AUS are given in Table 2. The av10 values are 2–18% higher than ERA5 for LAN but within −7% (pr-cv) and 10% (v850) for AUS. The latter coincides with a bias of +8% for vq and +9% for pr, consistent with the importance of moisture from the tropics to Australian rainfall. The spatial averages for tas, pr and psl of VAR averaged over the full ensemble (av35) are given in Table 3. They are within −2 and +5% of those from av10.
| av35 | Δ | Δ% | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N34 | LAN | AUS | N34 | LAN | AUS | N34 | LAN | AUS | ||
| VAR | ||||||||||
| tas | 0.945 | 0.964 | 0.952 | 0.098 | 0.016 | 0.065 | 10 | 2 | 7 | |
| pr | 1.529 | 0.719 | 0.807 | 0.756 | 0.064 | 0.052 | 49 | 9 | 6 | |
| psl | 0.592 | 1.077 | 1.091 | 0.043 | 0.005 | 0.014 | 7 | 0 | 1 | |
| VAR-NINO34 | ||||||||||
| tas | 0.903 | 0.235 | 0.271 | 0.100 | 0.030 | 0.071 | 11 | 13 | 26 | |
| pr | 1.093 | 0.166 | 0.223 | 0.574 | 0.026 | 0.033 | 53 | 16 | 15 | |
| psl | 0.471 | 0.290 | 0.518 | 0.033 | 0.030 | 0.044 | 7 | 10 | 8 | |
| VAR-PID | ||||||||||
| tas | 0.655 | 0.204 | 0.239 | 0.052 | 0.005 | 0.049 | 8 | 2 | 20 | |
| pr | 0.568 | 0.152 | 0.230 | 0.238 | 0.014 | 0.030 | 42 | 9 | 13 | |
| psl | 0.395 | 0.254 | 0.428 | 0.035 | 0.006 | 0.004 | 9 | 2 | 1 | |
First, av35 is the average of the 35-model CMIP6 ensemble for P1. The future change from these, each scaled to 2°C GW, and denoted Δ, is given along with this change as a percentage of the av35 P1 values. The quantities are surface air temperature (tas, °C), precipitation (pr, mm day−1), and mean sea level pressure (psl, hPa).
The average s.d., or VAR, for the ERA5 MDB mean pr series, the Fig. 1b case, is 0.54 mm day−1. This is given in Table S3, along with the pr climatological means and other statistics for the seven Australian regions, from ERA5, av10 and av35. The VAR of All-Australia (AAUS) pr in ERA5 (also given in Table 4) is 55% of the AUS (grid point) value in Table 2. The VAR of AAUS pr is 10% larger in av35 than in ERA5, whereas the mean pr is 27% larger.
| ERA5 | P1 | Δ | U | Δ% | ||
|---|---|---|---|---|---|---|
| VAR of index (°C) | ||||||
| NINO34 | 0.883 | 1.012 | 0.139 | 0.037 | 14 | |
| PID | 0.438 | 0.508 | 0.051 | 0.017 | 10 | |
| VAR of AAUS pr (mm day−1) | ||||||
| VAR | 0.397 | 0.438 | 0.043 | 0.010 | 10 | |
| VAR-NINO34 | 0.140 | 0.204 | 0.036 | 0.011 | 18 | |
| VAR-PID | 0.160 | 0.210 | 0.034 | 0.011 | 16 | |
Values are given for ERA5, the av35 for P1 and the av35 future change Δ for 2°C GW, dimensional, then as a percentage of the P1 value (Δ, %). The statistical uncertainty term U for the av35 change is given (see Section 4.1). Results for six Australian regions are in Table S3.
In summary, aside from that somewhat enhanced variability compared with ERA5, the M skill scores for av10 and the spatial averages support both av10 and av35 as providing credible simulations of overall variability in P1 for the quantities considered here.
3.Variability linked to modes
3.1. Mode indices
Representing modes of variability over the IP are two indices analysed by Watterson (2020, 2022). The NINO34 index is defined here as the SST averaged over the Niño3.4 box (5°S–5°N, 170°–120°W) relative to a centred 11-year running mean of SST averaged over 30°S–30°N, for each of the four seasons. This aims to counter the effect of forced warming, similarly to the approach of Van Oldenborgh et al. (2021). As for all analyses, within each 40-year period, any remaining linear trend is removed. The four-season average of NINO34 s.d., or VAR of NINO34, for P1 from each model is given in Table S1, along with the ensemble averages (and is plotted later). The av35 value of 1.01°C is 15% larger than that from ERA5, as given in Table 4, whereas the av10 value is 9% larger.
The second index, the Pacific–Indian Dipole or PID, is defined by the SST mean over PAC, the west equatorial Pacific (ocean points within 10°S–10°N, 150°E–160°W; see Fig. S1) minus that over IND, east Indian (15°S–5°N, 85–135°E). The four-season average s.d. is typically half that of NINO34 (see Table S1, Table 4). Although PID is correlated with NINO34 (reaching r = 0.8 for SON from ERA5), it tends to be more strongly linked with Australian rainfall, on account of its representation of Indian Ocean anomalies (see Watterson 2020).
3.2. Quantification of variability linked to an index
Following Watterson (2020) and many previous studies, the anomaly of a quantity y linked to an index x, say yx, is given by standard linear regression over a 40-year period, where y and x are detrended anomaly time series here. The resulting linked time series is as follows:
where b is the regression coefficient, given as follows:
where r is the usual correlation coefficient and σ indicates the s.d. Examples of such anomaly series for rainfall are given in Fig. 1. The ‘regression anomaly’ is the dimensional anomaly for a +1 s.d. anomaly of the index (rather than the normalised version), given by bσx. It is a standard amplitude for the variation of a quantity that is linked to the index and its magnitude is also the s.d. of the yx time series. In the case of AAUS pr in SON (Fig. 1a), the regression anomaly for NINO34 is −0.18 mm day−1, with r being −0.59. These statistics, if they are taken to represent a link over a much longer period, are uncertain. By standard theory, based on a sample of 40, the 90% range for the long-term or ‘true’ r in this case is −0.74 to −0.39. The criterion for significance at the 0.1 level is |r| = 0.26. The r for PID is −0.75, which suggests a stronger link than for NINO34. The focus of CMIP6 model results is the ensemble averages, which are statistically more certain. In any case, the magnitude of r also represents the ratio of the s.d. of the variation linked to the index to the net s.d. Of course, r2 is the fraction of variance linked to the index.
A quantification of overall variability linked to a mode index that is comparable with VAR is provided by the four-season average of the magnitude (absolute value) of each seasonal regression anomaly (being the corresponding s.d.). This is denoted VAR-index – not to be confused with the VAR of the index. If the variability in a season is entirely due to the mode, then the magnitude is the same as the s.d. Statistical uncertainty means VAR-index can be a small positive value even if there is no link (and a near-zero anomaly) in a long-term data set. In any case, the statistic is calculated for each model individually, which produces a result comparable with that for ERA5.
3.3. Mode patterns
The seasonal regression anomaly patterns of the NINO34 and PID modes were calculated for the full suite of variables and data over the P1 period. Although the details of the analysis may differ somewhat, the ERA5 anomalies for NINO34 and PID (among other indices) for the same variables as in Fig. 2 were analysed by Watterson (2020) and presented for several seasons. Watterson (2022) calculated anomalies for the CMIP6 models. Skill scores were calculated in the way described in Section 2.3. A presentation of the seasonal anomaly fields over the IP domain has been prepared for publication elsewhere. It is worthwhile noting that the models with good skill for NINO34 tend to have good skill for variability, particularly for the moisture variables. The correlation across the 10 models between the s.d. and NINO34 skills, for each variable, is included in Table 1. Values for moisture are between 0.6 and 0.9, averaging a little higher than for CLIM, whereas the values for PID average a little lower. This reflects the contribution of the modes to variability in at least some of the IP domain.
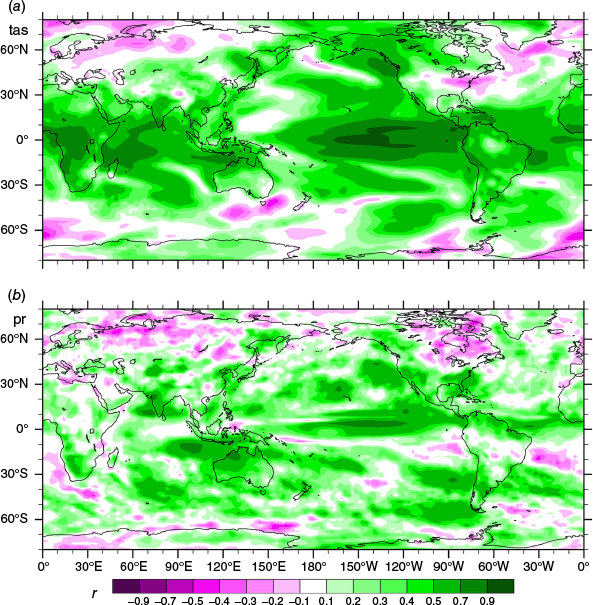
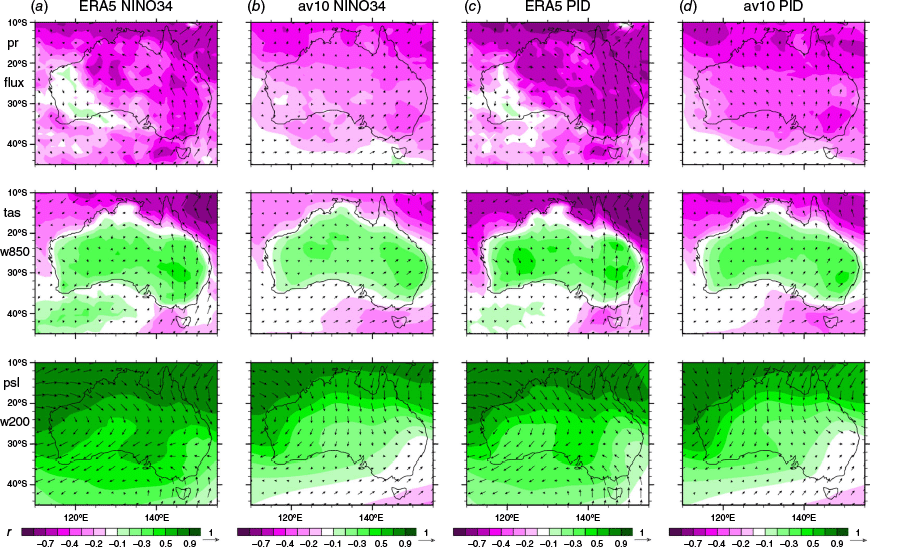
To focus on the contribution of mode anomalies to variability over Australia, and as further comparison of CMIP6 models with ERA5, the regional fields of r for the variables in Fig. 2 are depicted in Fig. 4, again for SON. Four cases are shown: for NINO34 from (a) ERA5, (b) av10 (the average of the r from the individual models), and for PID from (c) ERA5, (d) av10. The patterns are rather similar (consistent with the correlation between the indices in SON), with significantly negative r for pr and for tas over most surrounding seas, and positive r for tas over land and for psl. The anomalies of moisture flux and 850-hPa wind tend to be northward, especially over eastern Australia. The r values can be a little larger for ERA5 but av10 provides a more statistically certain result, with PID having a stronger link in pr over Australia. The plots for the other seasons are included in the Supplementary material (Fig. S3, S4 and S5). PID provides a stronger link for pr over the MDB in MAM (Fig. S4) and JJA (Fig. S5), consistent with the MDB results in Fig. 1b. In general, av10 provides a more uniform field over the continent, presumably owing to having less statistical variation (most evidently in DJF; Fig S3).
Correlation coefficient values (r) for the relationship between (detrended) seasonal mean index and quantities for SON over 1980–2019. The cases are: for NINO34 (a) ERA5, (b) av10 (the average over 10 CMIP6 models); for PID (c) ERA5, (d) av10. Shading shows values for (top) pr, (middle) tas, (bottom), psl. Vectors show values for vector quantities, eastward and northward components calculated separately: (top) flux, (middle) wind at 850 hPa, (bottom) wind at 200 hPa.
3.4. Overall variability (VAR-Index) in P1
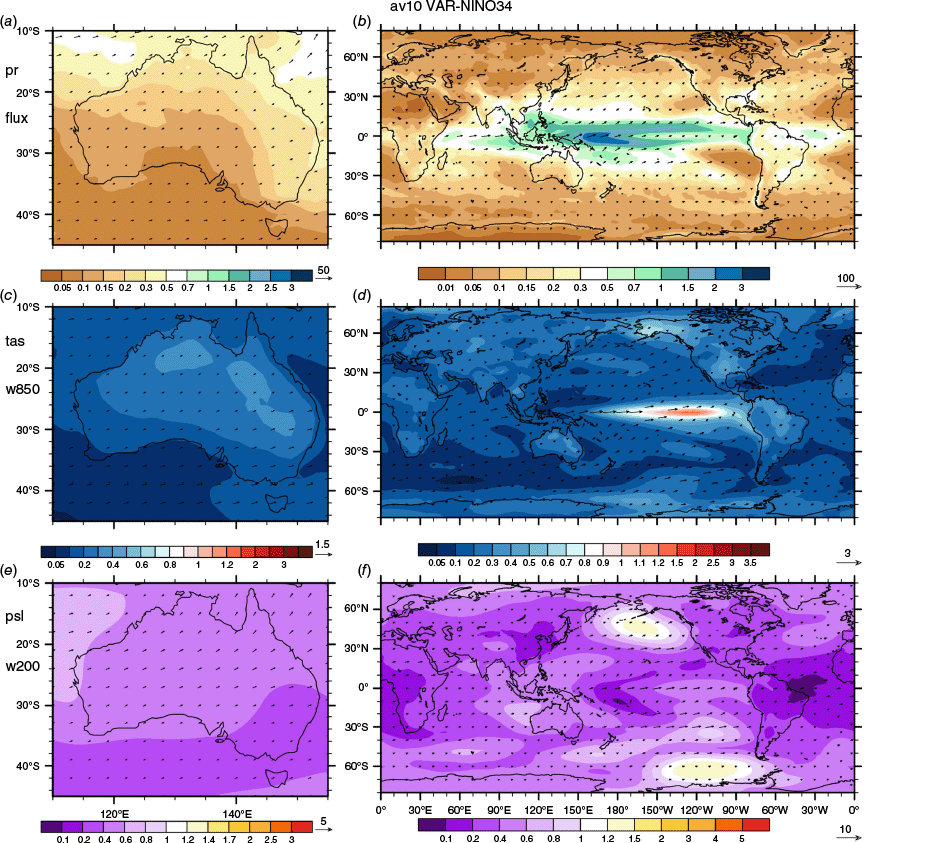
The average of VAR-NINO34 over 10 models, shown in Fig. 5, provides a similar spatial pattern to VAR (Fig. 3 for ERA5, Fig. S2 for av10) but the values at grid points over most of the globe are considerably smaller (Fig. 5 uses the same scales). An exception is the Niño3.4 box. The spatial averages over the box for tas, pr and psl from the full ensemble are given in Table 3. The VAR-NINO34 value for tas is 11% smaller than that of the index itself (using SST) and only 4% less than VAR tas. For psl, VAR-NINO34 is 80% of VAR over the box and for pr 71%. However, averaged over LAN and AUS (Table 3), VAR-NINO34 is less than 30% of VAR, except for 47% in the case of psl over AUS. For pr and moisture flux, much of the high VAR in the west equatorial Pacific is provided by VAR-NINO34 but elsewhere the flux and wind anomalies are barely visible in Fig. 5. For the PID index, the fields for av10 of VAR-PID are similar to those for NINO34 and are shown in Fig. S6. The values for pr and tas over Niño3.4 are smaller, and over the IND region a little larger, reflecting the index specification. The spatial averages for av35 are in Table 3.
As Fig. 3 but the overall variability linked to the NINO34 index in P1, VAR-NINO34, from av10. The value at each grid point is the four-season average of the magnitude (or absolute value) of the regression coefficient. The plots (a, c, e) for Australia use a 1° grid, and those for the globe (b, d, f), 2°. The regression coefficient is the anomaly for 1 s.d. of the index, using detrended series. The scales are as in Fig. 3.
Turning to pr averaged over the Australian regions, Table 4 gives the (net) VAR and VAR-index values for AAUS, for both ERA5 and av35. VAR-NINO34 is 35% of VAR for ERA5 and 47% for av35. The higher percentage, compared with that for grid points (28%, from Table 3), is consistent with the considerable coherence of the ENSO-related pr anomaly over the continent. The VAR-index to net VAR percentages are a little higher for PID. For regional averages (Table S3), the percentages peak with PID for South (46% for ERA5, 49% for av35). For av35, which provides a more statistically certain result, PID provides a higher percentage than NINO34 for South, SE (south-east) and MDB, and within 1% for the other regions. In short, for AAUS pr (Table 4), VAR-PID is a little larger than VAR-NINO34 in both ERA5 and CMIP6, and likewise for AUS (over grid points) in av35 (Table 3).
4.Future change in variability from CMIP6
4.1. Projection methodology
Following Watterson (2023), the years 2040–2079, denoted Period 2 or P2, from the simulation by each model for the scenario SSP5-8.5 were analysed. The global warming (GW), the change P2 – P1 in global mean tas, is given in Table S1 for each model. Following the traditional pattern scaling approach, for each statistic the change is divided by the GW (to form the ‘standardised change’), then multiplied by 2°C, to give a change representative of 2°C GW, denoted by Δ here, for each model. The corresponding future climate is denoted ‘fut2’. In fact, the ‘assessed’ GW of Lee et al. (2021) for P2 relative to P1, as a central estimate for the real world under SSP5-8.5, is ~2°C, based on their fig. 4.11d. Note that for the SSP3-7.0 scenario, with a smaller rise in radiative forcing, the assessed time for 2°C warming relative to P1 is later, c. 2071. The accuracy of the pattern scaling approach for variability and mode patterns has been less well assessed than for climate means. It is done here, in part, for consistency with the earlier analysis by Watterson (2023). In any case, the scaling factors (2°C ÷ GW) range from only 0.53 to 1.42, and the av35 patterns are very similar to the simple ensemble mean (of P2 – P1) reduced by the mean factor 0.81.
A standard approach for the projection of future change using models is to consider the ensemble mean as a central estimate of how the real world may change, in this case at the 2°C GW level. The range of results across the ensemble provides a plausible range for the real world, allowing for both ‘model uncertainty’ and internal variability. There remains statistical uncertainty associated with an average over even 35 models, particularly for change in variability. Under the idealised assumption that the n model values are normally distributed with standard deviation σ, uncertainty in the mean as representing the ‘true’ mean of a hypothetical much larger model ensemble can be based on the term:
In this case, σ is unknown and is estimated as the sample standard deviation of the n model values. Under standard statistical theory, the confidence level for the mean is then given by the t-distribution (with n − 1 degrees of freedom), which uses the same U. Using the one-sided t criterion for the 0.1 level, there is less than 10% chance of the true mean being of the opposite sign if the magnitude of the sample mean is more than 1.31U, the ‘statistical uncertainty criterion’. (The normal distribution factor is 1.28.) This is denoted ‘statistically certain in sign’. The full range of model values is considered in Section 5.
Given variation in variability (both s.d. and mode anomalies) across the four seasons in P1, there is naturally seasonal variation in the changes. For brevity, the focus is on the four-season averages. Seasonal changes in s.d. are briefly considered shortly.
4.2. Overall variability (VAR)
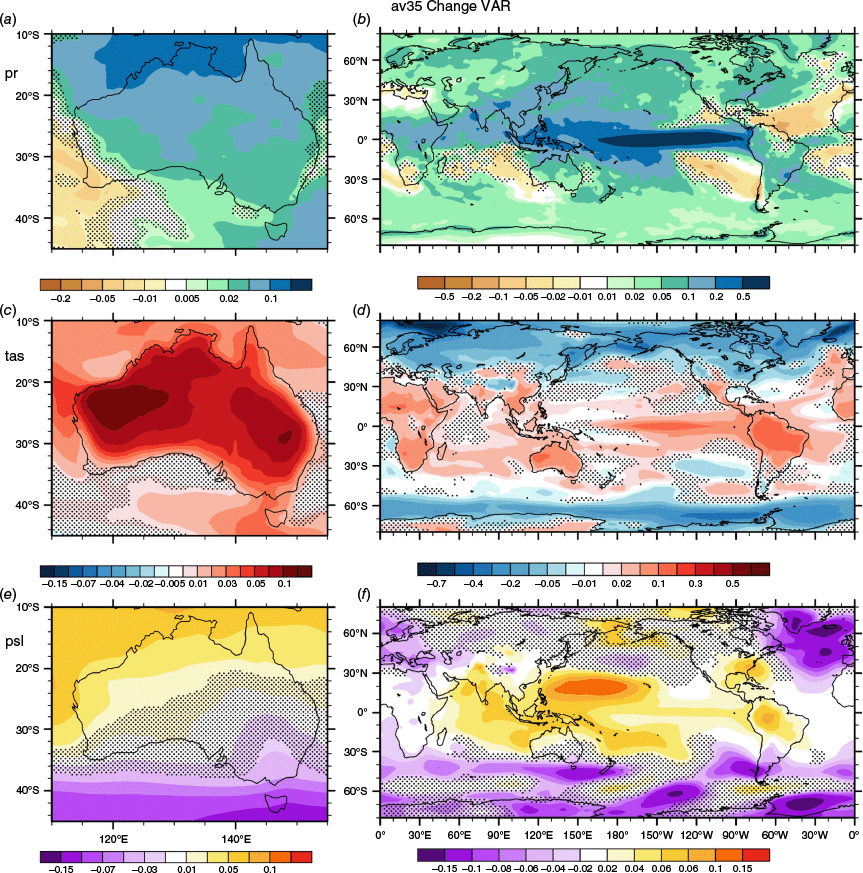
The av35 fields of change in overall (four-season average) variability (VAR) for pr, tas and psl are plotted in Fig. 6. To reiterate, here VAR is calculated for P2 using detrended seasonal series from each model, just as for P1. The change is then scaled to 2°C GW for each model. As an indication of statistical uncertainty, a change whose magnitude is less than 1.31U (as above) is stippled (unless both are smaller than the criterion for colour shading). In av35, the change in VAR in tas (Fig. 6c, d) is positive (i.e. VAR increases) over much of the low to mid latitudes, including Australia, reaching +0.1°C in the Australian interior. Poleward of ~50°N and 50°S, VAR mostly declines. As discussed by Lee et al. (2021), the causes include reductions in the gradient in mean temperature at high latitudes and sea ice retreat. Rainfall VAR (Fig. 6a, b) increases globally, except for the subtropical oceans where mean rainfall declines. There is no simple pattern for psl (Fig. 6e, f), with small increases in much of our IP domain, and some decreases at higher latitudes, where VAR is large in P1. In each plot, there are areas where the sign of the change is statistically uncertain but they are for relatively small values. The plots for av10, which include the vector quantities (in place of stippling), are shown in Fig. S7. The changes in pr, tas and psl at low latitudes, including over Australia, tend to be a little smaller than for av35. Among the vectors, the most prominent and widespread change is the increase in both components of moisture flux, consistent with increased water vapour (and integrated water, prw, shown by Watterson 2023) – the ‘thermodynamic’ effect of warming.
The change for 2°C GW in the overall variability of seasonal means (VAR) averaged over 35 CMIP6 models (denoted av35). Quantities and units are as in Fig. 2, with the scales reduced and vectors omitted. The shaded variables are: (a, b) pr (mm day−1); (c, d) tas (°C); and (e, f) psl (hPa). The vectors are (a, b) moisture flux (kg m−1 s−1); (c, d) wind at 850 hPa (m s−1); (e, f) wind at 200 hPa (m s−1), with reference vector length (for each vector component) shown. The stippling indicates where the magnitude of the change (of the ensemble average) is less than the statistical uncertainty criterion (1.31U), unless both are small (within the central, white band; see Section 4.1).
The changes in VAR for the nine variables plotted for av10 are given in Table 2, averaged over LAN and AUS, along with the changes as a percentage. The variables with the most notable changes are indeed the flux components, with increases from 7 to 16% of the P1 value. The LAN % increase for pr-cv is less than that for pr, presumably because the divisor (mean pr) tends to increase. (The pr-cv change is determined from the fut2 pr-cv for each model.) Averaged over AUS, though, the av10 of the change in pr-cv is 4%, more than for pr, whose mean change is typically small (e.g. Table S3). The av35 ΔVAR for tas, pr and psl, in Table 3, are 1 or 2% more positive than for av10 (Table 2), except for AUS tas, at 5% more and AUS pr at 4% more.
Turning to the changes in s.d. for individual seasons, for tas, the av35 changes in DJF and JJA compare well with the global patterns for CMIP6 shown by Lee et al. (2021) and noted earlier. Plots of changes for each season in tas, pr and psl for the Australian domain are included in Fig. S8. These changes are broadly like the four-season averages in Fig. 7, and differences are typically less certain in sign. Changes in rainfall variability in drier regions are smaller, whereas for temperature, the broad increase does not extend to the south in DJF and the north in SON. The s.d. for psl increases in JJA but decreases in the south-east in SON.
As Fig. 6 but the av35 change (future at 2°C GW – present, P1) in overall variability linked to the NINO34 index, VAR-NINO34. The shaded variables are: (a, b) pr (mm day−1); (c, d) tas (°C); and (e, f) psl (hPa). The vectors are (a, b) moisture flux (kg m−1 s−1); (c, d) wind at 850 hPa (m s−1); (e, f) wind at 200 hPa (m s−1), with reference vector length (for each vector component) shown.

4.3. Mode patterns (VAR-index)
The 2°C GW changes in the VAR of each index and model are given in Table S1. Most models give an increase for NINO34 and PID, with the av35 value given in Table 4. The increase for NINO34 is 14% of P1 but this falls to 4% for av10. The statistical uncertainty term U for the av35 change (Table 4) is a third or less of its value in each case. In calculating the future changes in variability linked to modes, the fut2 regression anomaly, at a grid point or for regional pr, was evaluated for each model, and the four-season average of the magnitude was then calculated. The change from the P1 VAR-index gives ΔVAR-index.
If there were no change in the mode pattern for a variable for 2°C GW, then the linked variability should change only in proportion to the change in the index s.d. The fields of av35 change in the overall variability linked to NINO34 (VAR-NINO34) are shown in Fig. 7, with the av10 results, including vectors, shown in Fig. S9. The patterns are similar but the increases for tas, pr and psl, over much of the tropics, are smaller in the av10 case, consistent with the smaller ΔVAR of NINO34. Furthermore, the changes in the tropics are mostly similar to the corresponding ΔVAR. The av35 of tas averaged over Niño3.4, given in Table 3, increases 11%, a little less than the index change, but very close to the ΔVAR for tas. The VAR-NINO34 increases there for pr and psl are nearly as large as the VAR increases. However, for pr, both increases are close to 50%, implying an amplification in the mode pattern there, as previously shown for CMIP5 models by Power et al. (2013). For LAN, the VAR-NINO34 percentage increases (Table 3) are close to that of the index. In the lower latitudes, ΔVAR-NINO34 (Fig. 7) seems to provide much of the change in VAR (Fig. 6) for tas and pr and often more than ΔVAR for psl. This holds for the AUS averages in Table 3. However, in far eastern Australia in av35 (Fig. 7a), VAR-NINO34 decreases. In mid and high latitudes in av35 (Fig. 6b), there are widespread increases in pr VAR along with some decreases, not due to NINO34. The changes in tas (Fig. 7d) and psl (Fig. 7f) from NINO34 are of both signs, although typically no more than 10% of the P1 values (Fig. 5d, f). These variations also indicate changes in the seasonal NINO34 patterns, such as presented by McGregor et al. (2022), although the effect on VAR-NINO34 is evidently complex.
The fields of av35 change in VAR-PID, shown in Fig. S10, resemble those for VAR-NINO34, but with mostly smaller magnitude, consistent with the smaller change in the index (ΔVAR of PID, Table 4). An exception is the change for pr over Australia, which is larger over the MDB for PID. The spatial averages of change included in Table 3 concur.
4.4. Australian regional precipitation
The 35-model average of 2°C GW change in VAR of AAUS pr (Table 4) represents an increase of 10%, with small statistical uncertainty. The ΔVAR-NINO34 for AAUS pr (Table 4) is similar to that for the AUS grid point result (Table 3). The percentage increases are also similar (18% for AAUS, 15% for AUS), and a little larger than the change in the index (14%). Of course, these comparisons mask seasonal and regional effects. As can be seen in Table S3, the percentage increases for VAR-NINO34 are larger for the North region (21%) than the MDB (5%) and SWWA (6%). The changes for PID (Table 4, Table S3) are similar to those for NINO34, despite the smaller index change. In summary, the CMIP6 ensemble average simulates a small increase in the overall interannual variability of precipitation and temperature over much of Australia, coinciding with a small increase in the variability of NINO34 and PID. There is a general increase in variability of moisture flux, consistent with increased atmospheric moisture.
5.Spread of results across the CMIP6 ensemble
5.1. Global patterns
The CMIP6 ensemble average fields provide evidence that variability in climate quantities may change under future warming. Some of the change may follow from a change in the modes, due to a change in the indices and in some cases the mode patterns. A projection of change in the real world for a future period would need to also represent its uncertainty. Based on the range of model results, even for these scaled to the 2°C GW level, this can be large. Note that the U statistic presented is only a sixth of the s.d. of the range. It is worthwhile trying to understand this range in the case of changes that are linked to the mode indices. Along with many comparable studies, Watterson (2019) showed that the standardised mean changes of pr, tas and psl from CMIP5 models can be well correlated across the ensemble with the mean change in mode indices, both at grid points and in regional averages. Typically, the spatial patterns for this correlation are like the mode patterns, such as those in Fig. 4. Such results may potentially support a constraint on projections, if the change in the index can be constrained. With our VAR-index quantity being based on the magnitude of the regression anomalies at 1 s.d. of the index, correlations with the index across the ensemble can be expected for the values from the P1 climate. It is interesting to test how well the link holds for changes in the four-season average.
Starting with NINO34, we consider first the link between the change in the index and the change in VAR-NINO34 of temperature at grid points. The model fields are first interpolated to a common 1° grid, as in forming av35. The field of correlation r across the 35 models between the point values for tas and the ΔVAR of NINO34 is shown in Fig. 8a. Not surprisingly, over Niño3.4 this exceeds 0.9, as the index closely determines the variability for each model (and even more so for SST). The correlation remains above 0.5 over most of the tropics, including much of Australia, and even into the mid latitudes, in regions where the av35 change (Fig. 7d) is (significantly) positive. Over most of the rest of the globe, r remains weakly positive, although with little significance, given that |r| = 0.28 is the criterion for significance at the 0.1 level, with n = 35. For the point values for pr, the correlation (Fig. 8b) is over 0.5 for Niño3.4 and north-west Australia, and some other regions, mostly where the av35 change (Fig. 7b) is significant. Elsewhere, there is no correlation. The corresponding fields for the PID index are shown in Fig. S11. The results are broadly similar to those in Fig. 8, although with somewhat smaller r values, especially over the Niño3.4 box. The correlations are mostly high over the PAC and IND regions, consistent with the index definition and the larger changes for av35 (Fig. S10). Again, the values for pr over much of Australia are higher than for NINO34, with r typically 0.4–0.6.
5.2. All-Australia rainfall
Given that the change in variability of pr that is linked to each index is positively correlated across the 35 models with the change in the index at most points over Australia, it is interesting to consider the relationships for the All-Australia spatial mean, AAUS pr. Using scatter plots allows values from the individual models to be illustrated, and it is worthwhile starting with the P1 values. For the indices, the values are those from Table S1.
In Fig. 9a, the P1 VAR-NINO34 values for AAUS pr are plotted (as y, in red) against the VAR of the NINO34 index (x). The regression line for the relationship is shown, spanning the model index range, along with the av35 mean values (from Table 4, P1). The correlation coefficient r = 0.64, shown on the plot, quantifies a good link, although with considerable scatter. The corresponding results for the PID index are in Fig. 9c. As for the link for interannual variability (e.g. Fig. 1a), PID has the higher correlation, with r = 0.85. The same holds for the net VAR, which is plotted in each panel (as y, in black), against the same index values. For each model and av35, VAR of AAUS pr is typically ~0.2 mm day−1 larger than VAR-index of AAUS pr. The regression line has a similar slope, with similar r, for both indices. The values for each statistic from ERA5 (as Table 4) are also plotted. These points lie near the regression line in each case. Hence, the higher values for av35, compared with ERA5, for both VAR and VAR-index are consistent with the somewhat greater variability of each index in av35. The ERA5 values are certainly well within the CMIP6 range.
Variability of All-Australia (AAUS) pr plotted against the variability of two indices from 35 models, left NINO34 and right PID. In each both the net variability VAR (in black) and the variability linked to the index VAR-index (in red) are plotted (as the y coordinate) against VAR of the index (as x). The mean of the 35 values of x and y is shown as a cross, matching the values given in Table 4. In (a, c), values are for the present (P1) climate, with values for ERA5 shown as a star, and in (b, d) for the change Δ, at 2°C GW. Also shown is the correlation (r) between the x and y values and the regression line for each case (spanning the x values). In (b, d), the mean change for AAUS pr explained by the regression (Δexp) from the mean change in the index is also given. The remaining change is the y-value of the regression line at x = 0.
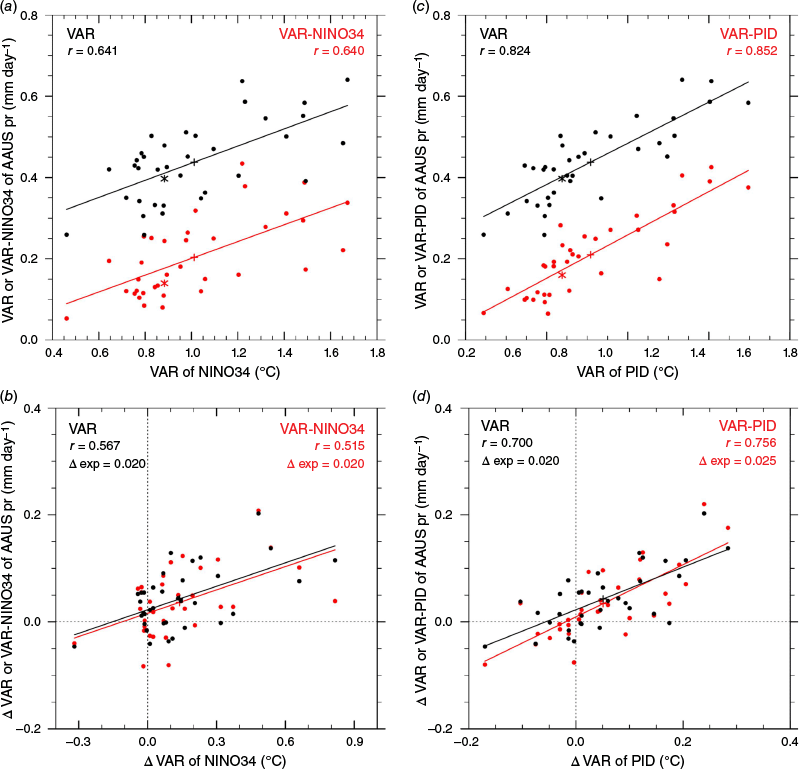
Returning to the changes for 2°C GW, the scatter plots and statistics for NINO34 are shown in Fig. 9b, and for PID, Fig. 9d. For each, there are changes of both signs from the models, although most are positive as are the av35 values. The av35 ΔVAR of AAUS pr is only a little larger (Table 4, Δ) than each ΔVAR-index of AAUS pr. The correlations (shown) range from 0.52 for ΔVAR-NINO34 to 0.76 for ΔVAR-PID. Based on the regression lines, a model with zero change in VAR of NINO34 could be expected to have a small increase in the variability of AAUS pr, both VAR and VAR-NINO34, matching the y-intercept at x = 0. This may represent the thermodynamic increase in rainfall variability. The remaining av35 change in y is the ‘change explained’ by the change in the index. The values for each case are given on the panels. For ΔVAR-PID of AAUS pr, this is 0.025 mm day−1, more than half the av35 change (0.034 mm day−1). The regression lines could also be used to refine a projection for AAUS pr, if the ΔVAR for an index was known with more certainty.
In summary, there is a considerable range of possible change in the variability of All-Australian rainfall, given model uncertainty and internal variability (for 40-year periods). Much of this range can be linked to the range of changes in the variability of NINO34 and PID, especially.
6.Conclusions
The variability of Australian and global climate is assessed using the observational ERA5 reanalysis for 1980–2019 and a data set of CMIP6 simulations for both that period and for 2040–2079 under the SSP5-8.5 scenario. Precipitation (pr), temperature and pressure (basic climate) are assessed from a 35-model ensemble, and winds and moisture variables are assessed from 10 models that supplied the vertically integrated horizontal moisture flux vector, as well as from ERA5.
The standard deviation (s.d.) of the detrended series of seasonal means within each 40-year period is calculated for grid points and for rainfall averaged over All Australia (AAUS pr) and six regions. The four-season average of s.d., or VAR, is a measure of overall variability. From ERA5, the average for grid points over Australia (AUS) is 4–11% higher than that from all land in 60°S–60°N (LAN) for each variable, except for moisture flux and 850-hPa eastward wind, at 31–41% higher. Australia is 54% higher for the coefficient of variation for precipitation.
The skill of 10 models in simulating the seasonal s.d. fields over the Indo-Pacific region is quantified using the M score, complementing a previous assessment of means. Again, HadGEM3-GC31-MM has the best model score for basic climate and for moisture variables but is surpassed by the 10-model average, av10.
The overall variability (VAR-index) linked to two mode indices, NINO34 and PID, is quantified by the four-season average of the magnitude of the regression anomaly at 1 s.d., calculated for each model individually. This provides values comparable with those from the observational series. The 35-model average (av35) of VAR-NINO34 averaged over AUS and LAN for precipitation, temperature and pressure is typically less than 30% of the net VAR. For AAUS pr, this rises to 47%, with VAR-PID higher again at 48%. There is much variability unrelated to the indices.
The statistics for the future period are scaled to provide a change representative of the 2°C global warming level. The most prominent change in VAR is for moisture variables, with an increase in precipitation from av10 of 2% for AUS and 8% for LAN, where flux increases 13–16%. However, av35 has a larger increase in precipitation: AUS 6%, LAN 9% and a remarkable 49% for the Niño3.4 box. This boost seems consistent with the larger increase in the VAR of the NINO34 index in av35, 14%, compared with 4% for av10. The VAR-NINO34 for precipitation increases 15% for AUS, 16% for LAN.
As for means, projections of change in future variability over a 40-year period need to include model uncertainty and statistical uncertainty. Both contribute to the range of results over the CMIP6 ensemble. The change in VAR-NINO34 for temperature over the Niño3.4 box is highly correlated across the 35 models with the change in VAR of the index. This falls away with distance but r ≈ 0.5 for temperature and rainfall at points in the mid latitudes that are linked to the index. The change in VAR of All-Australia rainfall (both for the mode and net) is more highly correlated with the VAR of PID, at r ≈ 0.7. These results based on CMIP6 appear to provide the basis for projections of the variability of seasonal means, with a central estimate of typically a 5–15% increase for Australian rainfall at 2°C global warming, in part due to increases in driver variability. Nevertheless, it should be emphasised that future changes in ENSO remain uncertain.
Data availability
The CMIP6 data that support this study are available from the Earth System Grid Federation at https://esgf-node.llnl.gov. Moisture flux data for HadGEM-GC31-LL and -MM were obtained directly from the UK Met Office. The ERA5 data are provided by the Copernicus Climate Change Service (2017) at https://cds.climate.copernicus.eu/cdsapp#!/home.
Acknowledgements
The author acknowledges the World Climate Research Programme, which, through its Working Group on Coupled Modelling, coordinated and promoted CMIP6. I thank the climate modelling groups for producing and making available their model output, the Earth System Grid Federation (ESGF) for archiving the data and the multiple funding agencies who support CMIP6 and ESGF. Most of the computational work was performed at NCI Australia. The skill score software was developed in collaboration with Roger Bodman. Calculations and plotting were largely performed using the NCL software (NCAR Command Language, NCAR, Boulder, CO, USA) and CDO (Climate Data Operators); see https://code.mpimet.mpg.de/projects/cdo. At time of writing, ‘Australia has a highly variable climate’ and ‘climate change is adding to Australia’s natural climate variability’ are stated on webpages of https://soe.dcceeew.gov.au/ and www.acs.gov.au, for example. I thank two anonymous reviewers for their very helpful comments.
References
Alexander LV, Uotila P, Nicholls N (2009) Influence of sea surface temperature variability on global temperature and precipitation extremes. Journal of Geophysical Research 114, D18116.
| Crossref | Google Scholar |
Bureau of Meteorology and CSIRO (2022) State of the Climate Report. (Commonwealth of Australia) Available at http://www.bom.gov.au/state-of-the-climate/2022/documents/2022-state-of-the-climate-web.pdf
Cai W, Ng B, Geng T, Jian F, Wu L, et al. (2023) Anthropogenic impacts on twentieth-century ENSO variability changes. Nature Reviews Earth and Environment 4, 407-418.
| Crossref | Google Scholar |
Chung C, Boschat G, Taschetto A, Narsey S, McGregor S, Santoso A, Delage F (2023) Evaluation of seasonal teleconnections to remote drivers of Australian rainfall in CMIP5 and CMIP6 models. Journal of Southern Hemisphere Earth System Science 73, 219-261.
| Crossref | Google Scholar |
Douville H, Raghavan K, Renwick J, Allan RP, Arias PA, Barlow M, Cerezo-Mota R, Cherchi A, Gan TY, Gergis J, Jiang D, Khan A, Pokam Mba W, Rosenfeld D, Tierney J, Zolina O (2021) Water Cycle Changes. In ‘Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change’. pp. 1055–1210. (Cambridge University Press) 10.1017/9781009157896.010
Gu G, Adler RF (2019) Precipitation, temperature, and moisture transport variations associated with two distinct ENSO flavors during 1979–2014. Climate Dynamics 52, 7249-7265.
| Crossref | Google Scholar |
Gutiérrez JM, Jones RG, Narisma GT, Alves LM, Amjad M, Gorodetskaya IV, Grose M, Klutse NAB, Krakovska S, Li J, Martínez-Castro D, Mearns LO, Mernild SH, Ngo-Duc T, van den Hurk B, Yoon J-H (2021) Atlas. In ‘Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change’. pp. 1927–2058. (Cambridge University Press) 10.1017/9781009157896.021
Hersbach H, Bell B, Berrisford P, et al. (2020) The ERA5 global reanalysis. Quarterly Journal of the Royal Meteorological Society 146, 1999-2049.
| Crossref | Google Scholar |
Holgate CM, Evans JP, van Dijk AIJM, Pitman AJ, Di Virgilio G (2020a) Australian precipitation recycling and evaporative source regions. Journal of Climate 33, 8721-8735.
| Crossref | Google Scholar |
Holgate CM, Van Dijk AIJM, Evans JP, Pitman AJ (2020b) Local and remote drivers of southeast Australian drought. Geophysical Research Letters 47(18), e2020GL90238.
| Crossref | Google Scholar |
Klingaman NP, Woolnough SJ, Syktus J (2013) On the drivers of inter-annual and decadal rainfall variability in Queensland, Australia. International Journal of Climatology 33, 2413-2430.
| Crossref | Google Scholar |
Lee J-Y, Marotzke J, Bala G, Cao L, Corti S, et al. (2021) Future Global Climate: Scenario-Based Projections and Near-Term Information. In ‘Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change’. pp. 553–672. (Cambridge University Press) 10.1017/9781009157896.006
Maher N, Jnglin Wills RC, Di Nezio P, Klavans J, Milinski S, Sanchez SC, Stevenson S, Stuecker MF, Wu X (2023) The future of the El Niño–Southern Oscillation: using large ensembles to illuminate time-varying responses. Earth System Dynamics 14, 413-431.
| Crossref | Google Scholar |
McGregor S, Cassou C, Kosaka Y, Phillips AS (2022) Projected ENSO teleconnection changes in CMIP6. Geophysical Research Letters 49, e2021GL097511.
| Crossref | Google Scholar |
McMahon TA, Peel MC, Vogel RM, Pegram GGS (2007) Global streamflows – part 3: country and climate zone characteristics. Journal of Hydrology 347, 272-291.
| Crossref | Google Scholar |
Nicholls N, Wong KK (1990) Dependence of rainfall variability on mean rainfall, latitude, and the Southern Oscillation. Journal of Climate 3, 163-170.
| Crossref | Google Scholar |
Pendergrass AG, Knutti R, Lehner F, Deser C, Sanderson BM (2017) Precipitation variability increases in a warmer climate. Scientific Reports 7, 17966.
| Crossref | Google Scholar | PubMed |
Power S, Delage F, Chung C, Kociuba G, Keay K (2013) Robust twenty-first-century projections of El Niño and related precipitation variability. Nature 502, 541-545.
| Crossref | Google Scholar | PubMed |
Scherrer SC (2011) Present-day interannual variability of surface climate in CMIP3 models and its relation to future warming. International Journal of Climatology 31, 1518-1529.
| Crossref | Google Scholar |
Schroeter S, Bi D, Law RM, Loughran TF, Rashid HA, Wang Z (2024) Global-scale future climate projections from ACCESS model contributions to CMIP6. Journal of Southern Hemisphere Earth System Science 74, ES23029.
| Crossref | Google Scholar |
Schubert SD, Stewart RE, Wang H, Barlow M, Berbery EH, et al. (2016) Global meteorological drought: a synthesis of current understanding with a focus on SST drivers of precipitation deficits. Journal of Climate 29, 3989-4019.
| Crossref | Google Scholar |
Seager R, Henderson N, Cane M (2022) Persistent discrepancies between observed and modeled trends in the tropical Pacific Ocean. Journal of Climate 35, 4571-4584.
| Crossref | Google Scholar |
Van Oldenborgh GJ, Hendon H, Stockdale T, L’Heureux M, Coughlan de Perez E, Singh R, van Aalst M (2021) Defining El Niño indices in a warming climate. Environmental Research Letters 16, 044003.
| Crossref | Google Scholar |
Watterson IG (2019) Indices of climate change based on patterns from CMIP5 models, and the range of projections. Climate Dynamics 52, 2451-2466.
| Crossref | Google Scholar |
Watterson IG (2020) Australian rainfall anomalies in 2018–2019 linked to Indo-Pacific driver indices using ERA5 reanalyses. Journal of Geophysical Research 125, e2020JD033041.
| Crossref | Google Scholar |
Watterson IG (2022) Atmospheric moisture anomalies associated with modes of variability and future changes. In ‘AMOS 2022 Conference’, 28 November–1 December 2022, Adelaide, SA, Australia. p. 72. (Australian Meteorological and Oceanographic Society) Available at http://hdl.handle.net/102.100.100/481740?index=1 [Abstract]
Watterson IG (2023) Atmospheric moisture transport associated with precipitation in present and simulated future climates. Journal of Climate 36, 6409-6425.
| Crossref | Google Scholar |
Watterson IG, Chua Z-W, Hope PK (2016) Extreme monthly rainfall over Australia in a changing climate. Journal of Southern Hemisphere Earth System Science 66, 402-423.
| Crossref | Google Scholar |
Watterson IG, O’Kane TJ, Kitsios V, Chamberlain MA (2021) Australian rainfall anomalies and Indo-Pacific driver indices: links and skill in 2-year-long forecasts. Journal of Southern Hemisphere Earth System Science 71, 303-319.
| Crossref | Google Scholar |