The duhka of DFT: a noble path to better functionals via a point electron approximation for the exchange–correlation hole†,‡
Dylan Jayatilaka A * and Amir Karton A *
A *
A School of Molecular Sciences, The University of Western Australia, Perth, WA 6009, Australia.
Australian Journal of Chemistry 75(11) 888-892 https://doi.org/10.1071/CH21332
Submitted: 14 December 2021 Accepted: 17 January 2022 Published: 28 March 2022
© 2022 The Author(s) (or their employer(s)). Published by CSIRO Publishing. This is an open access article distributed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License (CC BY-NC-ND)
Abstract
Density functional theory (DFT) is currently experiencing a golden age. The past two decades witnessed remarkable advances in the general applicability of density functionals in the top rungs of Jacob’s Ladder. Nevertheless, Jacob’s Ladder may have reached its highest rung in terms of dependencies on occupied (rung four) and unoccupied orbitals (rung five). Moreover, the fifth rung is associated with a computational cost far greater than the lower rungs. Another limitation is that each rung includes dozens of different functionals, and at present, there is no clear pathway for systematic improvements within each rung of the ladder. This highlight provides an overview of the exchange–correlation (XC) hole and how it could be used in developing new density functionals. We begin with a brief overview of the current status and challenges in developing better density functionals, followed by the intimate relationship between the XC functional and hole. We present a conceptually simple and computationally economical method for calculating the XC hole and how this method could offer new directions in developing better exchange–correlation functionals.
Keywords: density functional theory, electron correlation, exchange correlation energy, exchange correlation functional, exchange correlation hole, Jacob’s Ladder, pair correlation function.
Density functional theory
When it comes to predicting chemical properties, density functional theory (DFT) in its Kohn–Sham (KS) form is today unarguably the workhorse of quantum chemistry. This is due to its attractive accuracy-to-computational cost ratio. In short, DFT works well, and it will not break your bank of computers. DFT has this remarkable status because contrary to the methods based on wavefunctions that depend on every electronic coordinate, DFT depends on the electron density ρ – a function of only three coordinates, regardless of the number of electrons. Today, conventional DFT methods are routinely applicable to systems with hundreds of atoms and even to systems with millions of atoms using linear-scaling and orbital-free DFT techniques. (For a comprehensive review of large scale DFT calculations, see ref.1). We also note that DFT is the method of choice for generating massive amounts of chemical data needed for training machine learning models.[2]
Open secrets
However, everyone knows DFT’s dirty little secret. There are, in fact, two of them. The first is that the rarely-employed Hohenberg–Kohn (HK) version of DFT – the only version that depends explicitly on the electron density – is in practice a dismal failure when it comes to prediction of chemical properties. (This failure of HK-DFT was in fact the motivating reason for the more successful KS-DFT theory.)[3] The second, more often mentioned, is that DFT involves an unknown exchange–correlation (XC) functional which must be modelled somehow.[4–14] This incompleteness of DFT poses a fundamental limitation on the applicability and intrinsic accuracy of the theory and has led to a proliferation in the number of developed DFT methods over the past three decades, resulting in hundreds of different models for the XC functional.[8] From the point of view of the proverbial used-car salesperson then, DFT is an iconic example: it does not depend explicitly on its namesake, the electron density, and its contract is written without any guarantee of repair.[15]
A ladder to nirvana?
Into this density functional zoo, at the turn of the millennium, John Perdew shrewdly proposed his ‘Jacob’s Ladder of DFT’. In a loose analogy to John Pople’s two-dimensional diagram of systematically improved wavefunction methods,[16] Jacob’s Ladder provides a route where, with suitable effort, one might toil upwards towards the nirvana of chemically accurate functionals.[17]
The first rung of this ladder includes functionals that depend only on the value of the electron density through an energy density at a point in space, which itself depends only on the electron density at that same point, the so-called local density approximation (LDA). On the next rung is the generalised gradient approximation (GGA), which employs in addition the (reduced) gradient of the electron density at that point. By now you have the idea: the third rung, the meta-GGA (mGGA) functionals, employ in addition the second derivatives of the density at that point in the form of the Laplacian or the local kinetic energy density (the latter requiring not only the electron density but the KS orbitals themselves). This third rung is the last which can be regarded as ‘pure’ DFT, that is, DFT functionals that depend only on the electronic density and its gradients.
The fourth rung on the ladder involves admixing some component of the exact Hartree–Fock (HF) exchange. These functionals are therefore referred to as hybrid functionals. The fifth rung additionally involves admixing second-order Møller–Plesset perturbation theory (MP2) correlation energy. These functionals are referred to as double-hybrid DFT (DHDFT) functionals. The justification for these steps within the framework of DFT is the adiabatic connection formula of Harris and Jones.[18] Notwithstanding, it is hard to say that a combination of DFT with post-Hartree–Fock wavefunction theory really constitutes a DFT method at all; as Becke puts it, ‘I think KS-DFT is about occupied orbitals only’.[19]
Formally the computational cost of DHDFT methods is higher by 1–2 orders of magnitude relative to semi-local and hybrid DFT methods. The increase in computational cost of DHDFT relative to conventional DFT methods is further exacerbated by the need to use larger basis sets due to the slower basis set convergence of the MP2-like correlation term. Most chemical properties require at least a quadruple-zeta (ζ) quality basis set for obtaining results sufficiently close to the basis set limit.[10,20] Thus, a major disadvantage of functionals from the fifth rung of Jacob’s Ladder is that they are applicable to substantially smaller systems relative to functionals from the lower rungs.
Empirical or nonempirical?
Another useful way to classify DFT functionals is as being nonempirical or empirical. Nonempirical methods attempt to model the XC functional by satisfying known exact conditions.[21,22] Examples of popular nonempirical XC functionals are the GGA PBE,[23] meta-GGAs, TPSS[24] and SCAN,[25] hybrid-GGAs PBE0[26] and PBE0-1/3,[27] and hybrid-meta-GGA TPSSh.[28] Empirical methods, on the other hand, introduce parameters, which are determined by fitting to relevant thermodynamic, kinetic, and spectroscopic data obtained from experiment or more often from high-level ab initio wavefunction theory. Examples of popular highly empirical functionals with 10–40 adjustable parameters are the GGA HCTH407,[29] meta-GGAs τ-HCTH[30] and M06-L,[31] hybrid GGA B97-1, and hybrid-meta-GGAs BMK[32] and M06-2X.[33] As expected, empirical DFT methods tend to outperform nonempirical methods for chemical systems and properties that are covered in the training sets.[34–37] Nevertheless, this approach may lead to overfitting[38–40] and it has been found that heavily parameterised functionals may exhibit erratic basis set dependencies and grid sensitivity.[34,41–44] Thus, there is now a trend to develop empirical DFT functionals with a reduced number of parameters.[34,45–47] Interestingly, the ‘hyperparametric disorder’ of DFT was foreseen by Gill in an Essay published in the present journal two decades ago ‘Obituary: Density Functional Theory (1927–1993)’.[48] Still, we would caution, as von Barth does, regarding parameterisation, ‘There are certainly, theoreticians who would be prone to scorn the described [parameterisation] procedure but we find such attitudes unwise’.[5]
Considering the empirical nature of many generally applicable DFT methods along with the limitations of Jacob’s Ladder outlined above, such as the jump in computational cost of methods on the fifth rung relative to the lower rungs and lack of guidelines for systematic improvements within each of the rungs, it seems to us that DFT is in a state of existential dukha.[49] Is there a solution out of this fraught situation, a middle way?
The exchange–correlation hole
The concept of the exchange–correlation hole plays an important role in DFT. It is essentially the depression in the probability of finding an electron (with coordinates ‘r2’) around the position of a reference electron (labelled ‘r1’).
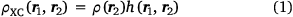
where by definition
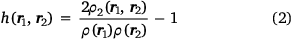
and where ρ2 is the second-order reduced density matrix.[3] From the above, we see that ρ(r1)ρXC(r1, r2) is the difference between the exact electron pair distribution and the classical distribution comprising a product of the electron densities of the two electrons. In the early days, Gunnarson and Lundqvist explain the success of LDA, the first rung, by casting it as an approximation to the exchange–correlation hole with the correct sum rule.[50] Importantly, the DFT exchange correlation energy EXC can be obtained very easily from a knowledge of the XC hole
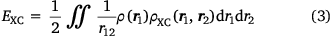
Thus, the functional of the exchange–correlation energy in terms of the exchange–correlation hole is known – a starting point not shared by the usual DFT functional of the electron density (where r12
Point electron approximation as a model to generate exchange–correlation holes
Obtaining the exchange correlation hole is challenging because it requires knowledge of the pair electron density, which, although obtainable from the wavefunction or quantum Monte Carlo calculations, is nevertheless computationally demanding, if not intractable for larger systems. There seem to be very few pictures of these in the literature, for example for H2 and Si(s).[57–59] From the existing images one learns that the exchange correlation hole is not spherical, and it extends onto nearby nuclei. This explains why a Taylor-series idea like the Jacob’s ladder scheme must necessarily be limited in its scope. We present here an idea to obtain a proxy for this quantity which is easier to calculate.
Suppose we have a program that can calculate a wavefunction for a given set of nuclei placed at some positions in space. The wavefunction may be as accurate as one desires HF, MP2, or CCSD (i.e. coupled cluster with single and double excitations). Consider now removing one electron from the system and placing it at a fixed position in space rfixed, just like the other nuclei in the system. If the program makes use of atom-centered basis sets, then place a basis set onto this electron. Next, solve the Schrödinger equation for the wavefunction of the remaining electrons. Then clearly, the electron density ρN–1(r1, rfixed) from this wavefunction is a very good proxy for ρ2(r1, rfixed) from which the exchange–correlation hole can be derived (Eqns 1, 2) (where N is the number of electrons in the original system).
Of course, this is not the exchange-correlation hole for the original system because one electron has been removed, but if the basis set on the electron is large, then one at least expects that the electron–electron cusp condition is well modelled – at least as well as the electron–nuclear cusp condition is on the remaining nuclei. One may collect as many of these pseudo exchange–correlation holes as one likes, simply by placing the fixed electron at distinct positions in space. From this, one can even calculate a pseudo exchange correlation energy via Eqn 3, integrating only over the coordinate of the first (unfixed) electron. Furthermore, placing the electron at the positions of a DFT integration grid would make it possible to integrate this quantity over all space, and calculate a pseudo electron–electron exchange correlation energy.
It is important to keep in mind that the pseudo exchange-correlation energy of the system with n–1 electrons calculated via a fixed electron as described above, will approach that of the real system with n electrons in the limit of a large number of electrons. Regardless of this limiting situation, we think that the pseudo exchange–correlation holes generated by this procedure form a simple, effective, and practical way to collect information pertaining to the real exchange correlation hole.
What to do with the information?
One idea immediately comes to mind. One can collect information concerning the exchange-correlation energy, the pointwise pseudo exchange-correlation energy from the procedure above, information about the electron density of the other electrons at the point of the reference electron (this is the ‘on-top’ pair density) as well as other quantities, such as the gradient of the electron density, the second derivative, the kinetic energy density, the asphericity of the exchange-correlation hole (parameterised by, say a spherical harmonic expansion), some notion of how the nuclei are arranged around the reference point, and the values of the electron density at the nuclear positions. A practical approach for processing these copious amounts of data would be through machine learning models. One may use this data to either improve DFT functionals using the standard Jacob’s ladder scheme (and then it will truly be at its limit) or one could model the actual exchange-correlation hole following the DFT pioneers.
Data availability
All data used for this article is available through the referenced literature.
Conflicts of interest
Amir Karton is an Associate Editor of the Australian Journal of Chemistry but was blinded from the peer-review process for this paper.
Declaration of funding
A. K. gratefully acknowledges an Australian Research Council (ARC) Future Fellowship (FT170100373). The authors thank Professor Jan Martin from the Weizmann Institute of Science for helpful discussions.
References
[1] LE Ratcliff, S Mohr, G Huhs, T Deutsch, M Masella, L Genovese, Wiley Interdiscip Rev Comput Mol Sci 2017, 7, e1290.| Crossref | GoogleScholarGoogle Scholar |
[2] GR Schleder, ACM Padilha, CM Acosta, M Costa, A Fazzio, J Phys Mater 2019, 2, 032001.
| Crossref | GoogleScholarGoogle Scholar |
[3] Parr RG, Yang W. Density Functional Theory of Atoms and Molecules. Oxford: Oxford University Press; 1989.
[4] P Geerlings, F De Proft, W Langenaeker, Chem Rev 2003, 103, 1793.
| 12744694PubMed |
[5] U von Barth, Phys Scr 2004, T109, 9.
| Crossref | GoogleScholarGoogle Scholar |
[6] F Neese, Coord Chem Rev 2009, 253, 526.
| Crossref | GoogleScholarGoogle Scholar |
[7] AJ Cohen, P Mori-Sánchez, W Yang, Chem Rev 2012, 112, 289.
| Crossref | GoogleScholarGoogle Scholar | 22191548PubMed |
[8] AD Becke, J Chem Phys 2014, 140, 18A301.
| Crossref | GoogleScholarGoogle Scholar | 24832308PubMed |
[9] R Peverati, DG Truhlar, Phil Trans R Soc A 2014, 372, 20120476.
| Crossref | GoogleScholarGoogle Scholar | 24516178PubMed |
[10] L Goerigk, S Grimme, Wiley Interdiscip Rev Comput Mol Sci 2014, 4, 576.
| Crossref | GoogleScholarGoogle Scholar |
[11] RO Jones, Rev Modern Phys 2015, 87, 897.
| Crossref | GoogleScholarGoogle Scholar |
[12] L Goerigk, N Mehta, Aust J Chem 2019, 72, 563.
| Crossref | GoogleScholarGoogle Scholar |
[13] P Verma, DG Truhlar, Trends Chem 2020, 2, 302.
| Crossref | GoogleScholarGoogle Scholar |
[14] JML Martin, G Santra, Isr J Chem 2020, 60, 787.
| Crossref | GoogleScholarGoogle Scholar |
[15] Some might say, “So what? Life comes with no guarantees.” Such was the nature of the schism that plagued quantum chemistry before the Great Reunification between Physicists and Chemists, the Nobel Prize of 1998.
[16] JA Pople, J Chem Phys 1965, 43, S229.
| Crossref | GoogleScholarGoogle Scholar |
[17] JP Perdew, K Schmidt, AIP Conf Proc 2001, 577, 1.
[18] J Harris, RO Jones, Phys F: Met Phys 1974, 4, 1170.
| Crossref | GoogleScholarGoogle Scholar |
[19] AD Becke, J Chem Phys 2014, 140, 18A301.
| Crossref | GoogleScholarGoogle Scholar | 24832308PubMed |
[20] A Karton, JML Martin, J Chem Phys 2011, 135, 144119.
| Crossref | GoogleScholarGoogle Scholar | 22010710PubMed |
[21] JP Perdew, A Ruzsinszky, J Tao, VN Staroverov, GE Scuseria, GI Csonka, J Chem Phys 2005, 123, 062201.
| Crossref | GoogleScholarGoogle Scholar |
[22] É Brémond, ÁJ Pérez-Jiménez, JC Sancho-García, C Adamo, J Chem Phys 2019, 150, 201102.
| Crossref | GoogleScholarGoogle Scholar | 31153220PubMed |
[23] JP Perdew, K Burke, M Ernzerhof, Phys Rev Lett 1996, 77, 3865.
| Crossref | GoogleScholarGoogle Scholar | 10062328PubMed |
[24] J Tao, JP Perdew, VN Staroverov, GE Scuseria, Phys Rev Lett 2003, 91, 146401.
| Crossref | GoogleScholarGoogle Scholar | 14611541PubMed |
[25] J Sun, A Ruzsinszky, JP Perdew, Phys Rev Lett 2015, 115, 036402.
| Crossref | GoogleScholarGoogle Scholar | 26230809PubMed |
[26] C Adamo, V Barone, J Chem Phys 1999, 110, 6158.
| Crossref | GoogleScholarGoogle Scholar |
[27] CA Guido, E Brémond, C Adamo, P Cortona, J Chem Phys 2013, 138, 021104.
| Crossref | GoogleScholarGoogle Scholar | 23320660PubMed |
[28] VN Staroverov, GE Scuseria, J Tao, JP Perdew, J Chem Phys 2003, 119, 12129.
| Crossref | GoogleScholarGoogle Scholar |
[29] AD Boese, NC Handy, J Chem Phys 2001, 114, 5497.
| Crossref | GoogleScholarGoogle Scholar |
[30] AD Boese, NC Handy, J Chem Phys 2002, 116, 9559.
| Crossref | GoogleScholarGoogle Scholar |
[31] Y Zhao, DG Truhlar, J Chem Phys 2006, 125, 194101.
| Crossref | GoogleScholarGoogle Scholar | 17129083PubMed |
[32] AD Boese, JML Martin, J Chem Phys 2004, 121, 3405.
| Crossref | GoogleScholarGoogle Scholar | 15303903PubMed |
[33] Y Zhao, DG Truhlar, Theor Chem Acc 2008, 120, 215.
| Crossref | GoogleScholarGoogle Scholar |
[34] N Mardirossian, M Head-Gordon, Mol Phys 2017, 115, 2315.
| Crossref | GoogleScholarGoogle Scholar |
[35] L Goerigk, A Hansen, C Bauer, S Ehrlich, A Najibi, S Grimme, Phys Chem Chem Phys 2017, 19, 32184.
| Crossref | GoogleScholarGoogle Scholar | 29110012PubMed |
[36] A Karton, S Daon, JML Martin, Chem Phys Lett 2011, 510, 165.
| Crossref | GoogleScholarGoogle Scholar |
[37] A Karton, Chem Phys 2021, 540, 111013.
| Crossref | GoogleScholarGoogle Scholar |
[38] MG Medvedev, IS Bushmarinov, J Sun, JP Perdew, KA Lyssenko, Science 2017, 355, 49.
| Crossref | GoogleScholarGoogle Scholar | 28059761PubMed |
[39] S Hammes-Schiffer, Science 2017, 355, 28.
| Crossref | GoogleScholarGoogle Scholar | 28059729PubMed |
[40] KP Kepp, Science 2017, 356, 496.
| Crossref | GoogleScholarGoogle Scholar | 28473557PubMed |
[41] ER Johnson, AD Becke, CD Sherrill, GA DiLabio, J Chem Phys 2009, 131, 034111.
| Crossref | GoogleScholarGoogle Scholar | 19624185PubMed |
[42] SE Wheeler, KN Houk, J Chem Theory Comput 2010, 6, 395.
| Crossref | GoogleScholarGoogle Scholar | 20305831PubMed |
[43] N Mardirossian, M Head-Gordon, J Chem Theory Comput 2013, 9, 4453.
| Crossref | GoogleScholarGoogle Scholar | 26589163PubMed |
[44] L-J Yu, F Sarrami, A Karton, RJ O’Reilly, Mol Phys 2015, 113, 1284.
| Crossref | GoogleScholarGoogle Scholar |
[45] N Mardirossian, M Head-Gordon, Phys Chem Chem Phys 2014, 16, 9904.
| Crossref | GoogleScholarGoogle Scholar | 24430168PubMed |
[46] N Mardirossian, M Head-Gordon, J Chem Phys 2015, 142, 074111.
| Crossref | GoogleScholarGoogle Scholar | 25702006PubMed |
[47] G Santra, N Sylvetsky, JML Martin, J Phys Chem A 2019, 123, 5129.
| Crossref | GoogleScholarGoogle Scholar | 31136709PubMed |
[48] PMW Gill, Aust J Chem 2001, 54, 661.
| Crossref | GoogleScholarGoogle Scholar |
[49] The word kha in dukha (which is the Sanskrit for suffering) was originally the word for “hole”.
[50] O Gunnarsson, BI Lundqvist, Phys Rev B 1976, 13, 4274.
| Crossref | GoogleScholarGoogle Scholar |
[51] O Gunnarsson, M Jonson, BI Lundqvist, Solid State Commun 1977, 24, 765.
| Crossref | GoogleScholarGoogle Scholar |
[52] R Colle, O Salvetti, Theor Chim Acta 1975, 37, 329.
| Crossref | GoogleScholarGoogle Scholar |
[53] C Lee, W Yang, RG Parr, Phys Rev B 1988, 37, 785.
| Crossref | GoogleScholarGoogle Scholar |
[54] AD Becke, MR Roussel, Phys Rev A 1989, 39, 3761.
| Crossref | GoogleScholarGoogle Scholar |
[55] AD Becke, ER Johnson, J Chem Phys 2005, 122, 154104.
| Crossref | GoogleScholarGoogle Scholar | 15945622PubMed |
[56] EJ Baerends, Phys Rev Lett 2001, 87, 133004.
| Crossref | GoogleScholarGoogle Scholar | 11580585PubMed |
[57] KJH Giesbertz, R van Leeuwen, U von Barth, Phys Rev A 2013, 87, 022514.
| Crossref | GoogleScholarGoogle Scholar |
[58] J Brüggemann, CR Jacob, Faraday Discuss 2020, 224, 56.
| Crossref | GoogleScholarGoogle Scholar | 32914802PubMed |
[59] RQ Hood, MY Chou, AJ Williamson, G Rajagopal, RJ Needs, WMC Foulkes, Phys Rev Lett 1997, 78, 3350.
| Crossref | GoogleScholarGoogle Scholar |
† Invited award contribution for the 2021 Citation Award (awarded to A.K.).
‡ The word kha in dukha (which is the Sanskrit for suffering) was originally the word for ‘hole’. We take it as a good omen.


