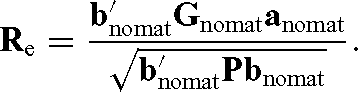The importance of accounting for maternal genetic effects in Australian fine-wool Merino breeding
M. Asadi Fozi A C D E , J. H. J. Van der Werf A C and A. A. Swan B CA The Institute for Genetics and Bioinformatics, School of Rural Science and Agriculture, University of New England, Armidale, NSW 2351, Australia.
B CSIRO Livestock Industries, Armidale, NSW 2350, Australia.
C Australian Sheep Industry CRC, Chiswick New England Highway, Locked Bag 1, Armidale, NSW 2350, Australia.
D Department of Animal Science, Faculty of Agriculture, University of Kerman, Kerman, Iran.
E Corresponding author. Email: masadifo@une.edu.au
Australian Journal of Agricultural Research 56(8) 789-796 https://doi.org/10.1071/AR05006
Submitted: 24 January 2005 Accepted: 8 June 2005 Published: 25 August 2005
Abstract
(Co) variances for greasy fleece weight (GFW), clean fleece weight (CFW), mean fibre diameter (MFD), staple strength (SS), coefficient of variation of fibre diameter (CVFD), birthweight (BW), weaning weight (WW), and yearling weight (YW) were estimated for 5108 Australian Merino sheep from the CSIRO Fine Wool Project, born between 1990 and 1994. Covariances between these traits and number of lambs weaned per ewe joined (NLW) were also estimated. Significant maternal genetic effects were found for GFW, CFW, BW, WW, and YW. Estimates of heritability were biased upwardly when maternal effects were ignored. The maternal heritability estimates for GFW, CFW, BW, WW, and YW were 0.17, 0.15, 0.38, 0.28, and 0.13, respectively. Maternal effects were not important for MFD, CVFD, SS, and NLW. Direct-maternal genetic correlations within each fleece weight and bodyweight trait were estimated to be moderately negative (–0.26 to –0.48). The effect of ignoring maternal genetic effect was explored using selection index theory. Accounting for the maternal effects in both the selection criteria and breeding objective increased the overall response by 14.3%, 4.8%, 2.6%, 1.4%, and 0.0% in 3, 6, 12, 20 and 30% micron premium scenarios, respectively, compared with when the maternal effects were only included in breeding objective. Complete ignorance of the maternal effects led to overestimation in overall response of 2.8–35.7% for different micron premium scenarios in contrast to when the maternal effects were ignored in the selection index weight, but were included in the breeding objective. The results indicate that the maternal genetic effects of fleece weight and bodyweight should be considered in Merino breeding programs.
Additional keywords: sheep, genetic parameters, wool traits, selection index.
Acknowledgment
We are grateful to CSIRO for providing us data from the Fine Wool Project.
Gilmour, AR ,
Gogel, BJ ,
Cullis, BR ,
Welham, SJ ,
and
Thompson, R (2002).
Hickson JD,
Swan AA,
Kinghorn PB, Piper LR
(1995) Maternal effects at different age in Merino sheep. Proceedings of the Association for the Advancement of Animal Breeding and Genetics 11, 416–420.

Lynch, M ,
and
Walsh, B (1998).
Maniatis N, Pollott GE
(2003) The impact of data structure on genetic (co)variance components of early growth in sheep, estimated using animal model with maternal effects. Journal of Animal Science 81, 101–108.
| PubMed |

Mortimer SI
(1987)
Mortimer SI, Atkins KD
(1994) Direct additive and maternal genetic effects on wool production of Merino sheep Proceeding of the 5th World Congress on Genetics Applied to Livestock Production 18, 103–106.

Mortimer SI, Atkins KD
(1995) Maternal effects influence growth traits in Merino sheep. Proceedings of the Association for the Advancement of Animal Breeding and Genetics 11, 421–424.

Notter D,
Tier B, Meyer K
(1992) Sirex herd interactions of weaning weight in beef cattle. Journal of Animal Science 70, 2359–2365.
| PubMed |

Purvis IW, Swan AA
(1997) Can follicle density be used to enhance the rate of genetic improvement in Merino flocks? Proceedings of the Association for the Advancement of Animal Breeding and Genetics 12, 512–515.

Robinson DL
(1996) Models which might explain negative genetic correlation between direct and maternal effects. Livestock Production Science 45, 111–122.
| Crossref | GoogleScholarGoogle Scholar |

Safari E,
Fogarty NM, Gilmour AR
(2005) A review of genetic parameter estimates for wool, growth, meat and reproduction traits in sheep. Livestock Production Science 92, 271–289.
| Crossref | GoogleScholarGoogle Scholar |

Swan AA, Hickson JD
(1994) Maternal effects in Australian merinos Proceeding of the 5th World Congress on Genetics Applied to Livestock Production 18, 143–146.

Swan AA, Purvis IW, Piper LR, Lamb PR, Robinson GA
(2000) The CSIRO fine wool project. ‘Background Objectives Fine wool 2000: Proceedings of Symposium’. 27–28 October 2000, Armidale, NSW. (CSIRO Livestock Industries and The Woolmark Company)
Vaez Torshizi R,
Raadsma HW, Nicholas FW
(1995) An investigation of the potential for early (indirect) selection in Australian Merino sheep. Proceedings of the Association for the Advancement of Animal Breeding and Genetics 11, 314–317.

van Wyk JB,
Erasmus GJ, Oliver JJ
(1994) Variance component estimates and response to selection on BLUP of breeding values in Merino sheep Proceeding of the 5th World Congress on Genetics Applied to Livestock Production 18, 31–34.

The breeding objectives were defined as:
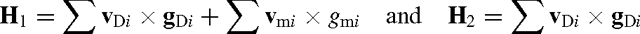
where H 1 is the breeding objective with maternal effects, v Di is direct relative economic value of the ith objective trait, g Di is the relative economic value of the ith maternal objective trait, and g mi is the breeding value of the ith maternal objective trait, and H 2 is the breeding objective without maternal effects.
The optimum response was calculated using the following equation:
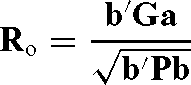
where b is a vector with selection index weights calculated as P −1 Ga when maternal genetic effects as well as direct additive genetic effects were considered, G is a matrix of genetic covariances between the selection criteria and breeding objectives containing direct and maternal components, a is a vector of direct and maternal relative economic values, and P is phenotypic co(variance) matrix.
The elements of G = (Gd Gm) are derived as follows:
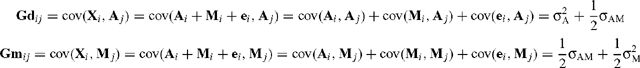
where X i is the phenotypic observation for trait i, A i is the direct additive genetic effect, M i is the maternal genetic effect, e i is the residual for trait i, and subscript j refers to these effects for trait j (measured on same animal).
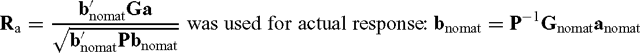
where G nomat is genetic covariance matrix when maternal genetic effects were ignored. The variance components that were used in the Gnomat were obtained from a model without fitting maternal genetic effects; anomat is a vector of direct relative economic values (subset of a).
Expected response was calculated using the equation: