Theoretical considerations about carbon isotope distribution in glucose of C3 plants
Guillaume Tcherkez A D , Graham Farquhar B , Franz Badeck C and Jaleh Ghashghaie AA Laboratoire d'écophysiologie végétale, UMR 8079, Bât. 362, Centre scientifique d’Orsay, Université Paris XI, 91405 Orsay Cedex, France.
B Research School of Biological Sciences, Institute of Advanced Studies, Australian National University, GPO Box 475 Canberra, ACT 2601, Australia.
C Potsdam Institute for Climate Impact Research (PIK), PF 60 12 03, 14412 Potsdam, Germany.
D Corresponding author; email: guillaume.tcherkez@ese.u-psud.fr
Functional Plant Biology 31(9) 857-877 https://doi.org/10.1071/FP04053
Submitted: 12 March 2004 Accepted: 20 July 2004 Published: 23 September 2004
Abstract
The origin of the non-statistical intramolecular distribution of 13C in glucose of C3 plants is examined, including the role of the aldolisation of triose phosphates as proposed by Gleixner and Schmidt (1997). A modelling approach is taken in order to investigate the relationships between the intramolecular distribution of 13C in hexoses and the reactions of primary carbon metabolism. The model takes into account C–C bond-breaking reactions of the Calvin cycle and leads to a mathematical expression for the isotope ratios in hexoses in the steady state. In order to best fit the experimentally-observed intramolecular distribution, the values given by the model indicate that (i), the transketolase reaction fractionates against 13C by 4–7‰ and (ii), depending on the photorespiration rate used for estimations, the aldolase reaction discriminates in favour of 13C by 6‰ during fructose-1,6-bisphosphate production; an isotope discrimination by 2‰ against 13C is obtained when the photorespiration rate is high. Additionally, the estimated fractionations are sensitive to the flux of starch synthesis. Fructose produced from starch breakdown is suggested to be isotopically heavier than sucrose produced in the light, and so the balance between these two sources affects the average intramolecular distribution of glucose derived from stored carbohydrates. The model is also used to estimate photorespiratory and day respiratory fractionations that appear to both depend only weakly on the rate of ribulose-1,5-bisphosphate oxygenation.
Keywords: Calvin cycle, isotope effects, photorespiration, respiration, starch.
Acknowledgments
We thank to Gabriel Cornic for his advice on writing the manuscript. Graham Farquhar acknowledges the Autralian Research Council for its support through a Discovery Grant. This work was supported in part by the European Community's Human Potential Program under contract HPRN-CT 1999–00059, [NETCARB].
Brugnoli E, Farquhar GD
(2000) Photosynthetic fractionation of carbon isotopes. ‘Photosynthesis, physiology and metabolism’. (Eds RC Leegood, TD Sharkey, S von Caemmerer)
pp. 399–434. (Kluwer Academic Publishers: Dordrecht)
Brugnoli E,
Hubick KT,
von Caemmerer S,
Wong SC, Farquhar GD
(1988) Correlation between the carbon isotope discrimination in leaf starch and sugars of C3 plants and the ratio of intercellular and atmospheric partial pressures of carbon dioxide. Plant Physiology 88, 1418–1424.
measured isotope ratios result from storage (root storage in beet, grain storage in maize) and so are derived from both light-produced (cytosolic) and night-produced Suc (transitory starch). The proportion of Glc that comes from light-produced Suc in storage Glc is denoted as L. From the relationships given before, it is deduced that the isotope ratios in the Glc analysed by Rossmann et al. (1991) are the following:
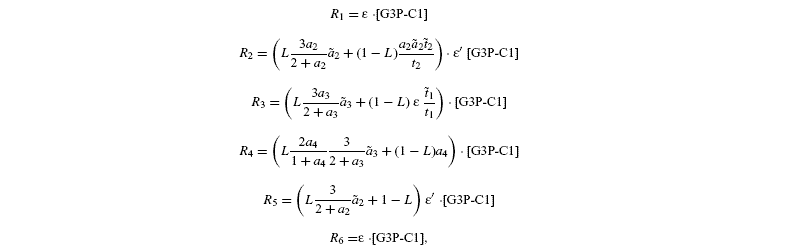
where [G3P-C1] is the isotope ratio of G3P in the chloroplast and is given by the relationship shown in Introducing starch synthesis. Those expressions do not allow a direct resolution and a linearisation is more convenient. The inverse isotope effects are written as ai=1+o(ai) so that the isotope discrimination is then Δ(ai)=1 / / ai-1 that is, –o(ai). If the second order terms in the previous equations are neglected, the discriminations are given by:
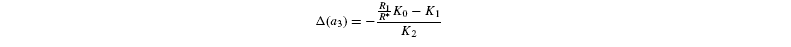
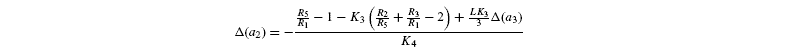
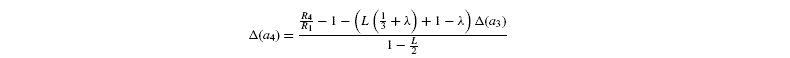
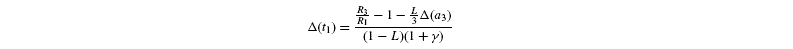
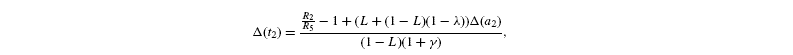
with the relationships:
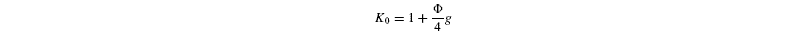
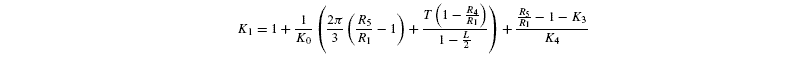
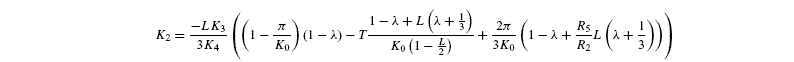
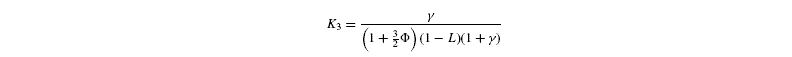
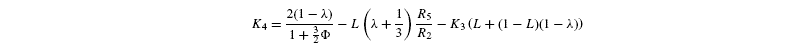
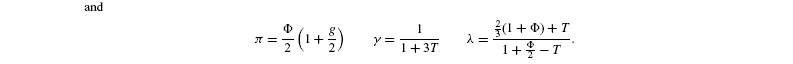
Photorespiratory discrimination
Isotope discrimination occurring during photorespiration in on-line gas-exchange systems is defined using net assimilated carbon as a reference material (Farquhar et al. 1982) and is equal to
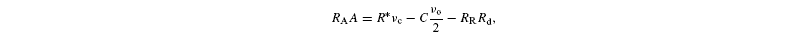
where A is the net assimilation rate, RR the carbon isotope ratio of day-respired CO2 and Rd the rate of day respiration. C is the isotope ratio in photorespired CO2 (see above). Rearranging, gives:
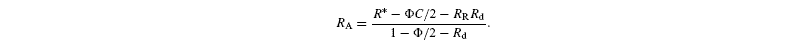
Assuming that G3P molecules entering glycolysis are completely degraded through respiration, RR is the mean isotope ratio in cytoplasmic G3P. The value of Rd is positive and its maximal value is E / 3 (Scheme 1). With the relationship C=2[RuBP-C2] / (2 + g) (see above) and neglecting second order terms, we get the approximation


